文档讲解:代码随想录
状态:已完成
513.找树左下角的值
思路
递归
分析一下题目:在树的最后一行找到最左边的值。
首先要是最后一行,然后是最左边的值。
如果使用递归法,如何判断是最后一行呢,其实就是深度最大的叶子节点一定是最后一行。
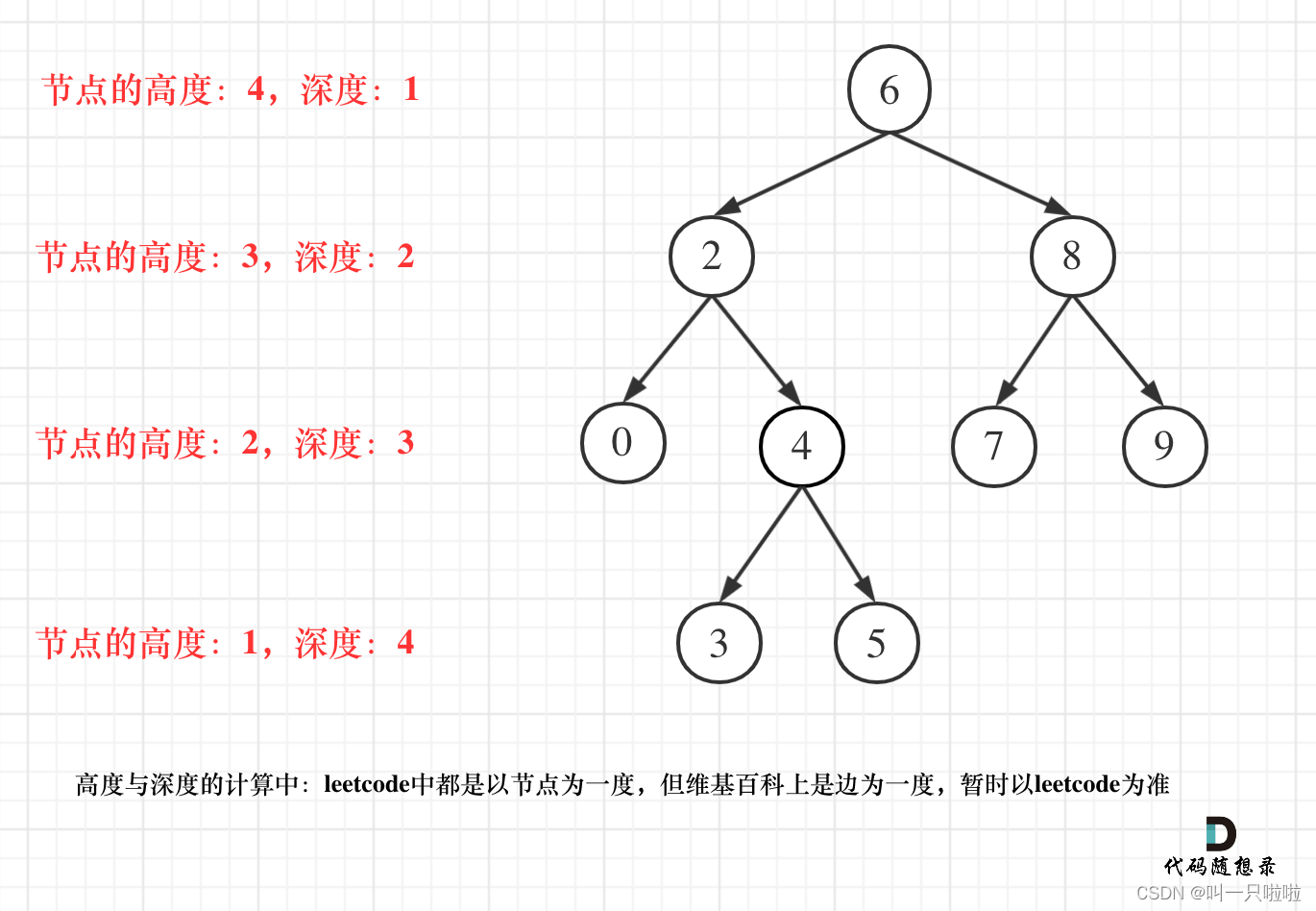
所以要找深度最大的叶子节点。
那么如何找最左边的呢?可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索【重点,因为优先搜索左边,当叶子节点不只有一个的时候,他会先搜索左边,将深度及值记录下来,之后再遇到相同深度的叶子就直接跳过了】,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
递归三部曲:
- 1.确定递归函数的参数和返回值
参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为void。
本题还需要类里的两个全局变量,maxLen用来记录最大深度,result记录最大深度最左节点的数值。
代码如下:
int maxDepth = Integer.MIN_VALUE;
int result = Integer.MIN_VALUE;
void findLeftVal(TreeNode node ,int depth)
- 2.确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
代码如下:
//终止条件
if (node.left == null && node.right == null){
if (depth > maxDepth){
maxDepth = depth;
esult = node.val;
}
return ;
}- 3.确定单层递归的逻辑
在找最大深度的时候,递归的过程中依然要使用回溯,代码如下:
// 中
//左
if (node.left != null){
depth++;
findLeftVal(node.left,depth);
depth--;
}
//右
if (node.right != null){
depth++;
findLeftVal(node.right,depth);
depth--;
}
return;完整代码如下:
class Solution {
int maxDepth = Integer.MIN_VALUE;
int result = Integer.MIN_VALUE;
public int findBottomLeftValue(TreeNode root) {
if (root == null){
return 0;
}
findLeftVal(root,1);
return result;
}
void findLeftVal(TreeNode node ,int depth){
//终止条件
if (node.left == null && node.right == null){
if (depth > maxDepth){
maxDepth = depth;
result = node.val;
}
return ;
}
//左
if (node.left != null){
depth++;
findLeftVal(node.left,depth);
depth--;
}
//右
if (node.right != null){
depth++;
findLeftVal(node.right,depth);
depth--;
}
}
}112. 路径总和
思路
递归
可以使用深度优先遍历的方式(本题前中后序都可以,无所谓,因为中节点也没有处理逻辑)来遍历二叉树
- 1.确定递归函数的参数和返回类型
参数:需要二叉树的根节点,还需要一个计数器,这个计数器用来计算二叉树的一条边之和是否正好是目标和,计数器为int型。
再来看返回值,递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(这种情况就是本文下半部分介绍的113.路径总和ii)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍)
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(本题的情况)
而本题我们要找一条符合条件的路径,所以递归函数需要返回值,及时返回,那么返回类型是什么呢?
如图所示:
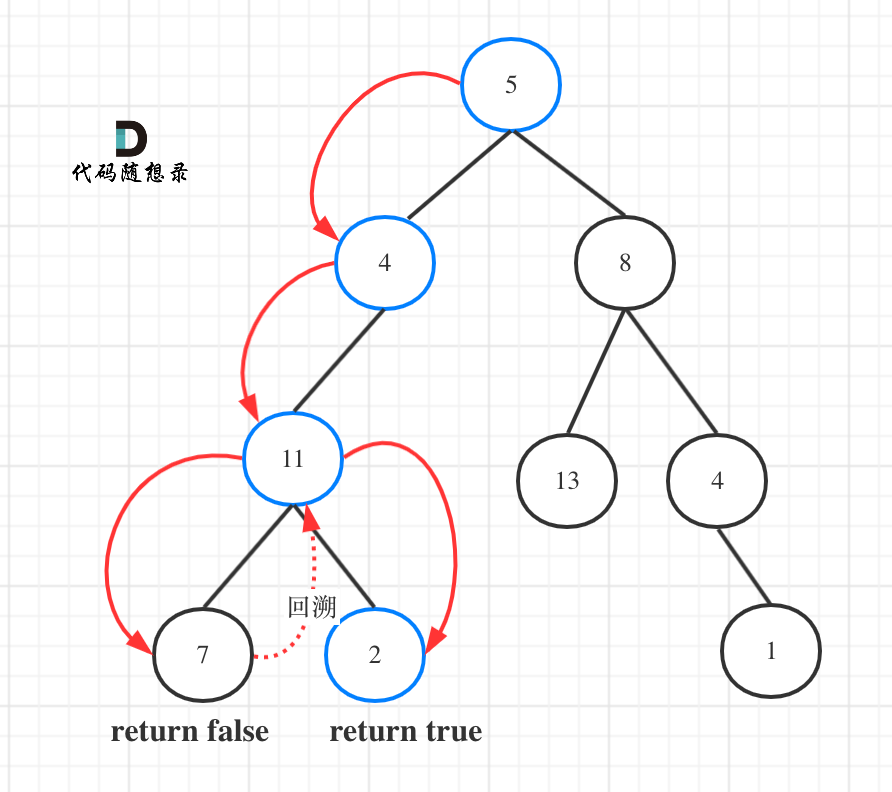
图中可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。
中可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。
所以代码如下:
boolean findTargetNum(TreeNode node,int sum,int targetSum) // 注意函数的返回类型
- 2.确定终止条件
首先计数器如何统计这一条路径的和呢?
我选择去累加然后判断是否等于目标和,if叶子节点中出现 sum == targetNum 就返回true
递归终止条件代码如下:
// 遇到叶子节点而没有找到合适的边,直接返回
if (node.left == null && node.right == null){
return sum == targetSum;
}
- 3.确定单层递归的逻辑
因为终止条件是判断叶子节点,所以递归的过程中就不要让空节点进入递归了。
递归函数是有返回值的,如果递归函数返回true,说明找到了合适的路径,应该立刻返回。
代码如下:
if (node.left != null){ //左
// 遇到叶子节点返回true,则直接返回true
// 注意这里有回溯的逻辑
sum += node.left.val;
boolean boolLfet = findTargetNum(node.left, sum, targetSum);
if (boolLfet){
return true;
}
sum -= node.left.val;
}
if (node.right != null){//右
// 遇到叶子节点返回true,则直接返回true
// 注意这里有回溯的逻辑
sum += node.right.val;
boolean boolRight = findTargetNum(node.right, sum, targetSum);
if (boolRight){
return true;
}
sum -= node.right.val;
}
return false;以上代码中是包含着回溯的.
代码如下:
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null){return false;}
return findTargetNum(root,root.val, targetSum);
}
boolean findTargetNum(TreeNode node,int sum,int targetSum){
if (node.left == null && node.right == null){
return sum == targetSum;
}
if (node.left != null){ //左
// 遇到叶子节点返回true,则直接返回true
// 注意这里有回溯的逻辑
sum += node.left.val;
boolean boolLfet = findTargetNum(node.left, sum, targetSum);
if (boolLfet){
return true;
}
sum -= node.left.val;
}
if (node.right != null){//右
// 遇到叶子节点返回true,则直接返回true
// 注意这里有回溯的逻辑
sum += node.right.val;
boolean boolRight = findTargetNum(node.right, sum, targetSum);
if (boolRight){
return true;
}
sum -= node.right.val;
}
return false;
}
}106.从中序与后序遍历序列构造二叉树
思路
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:
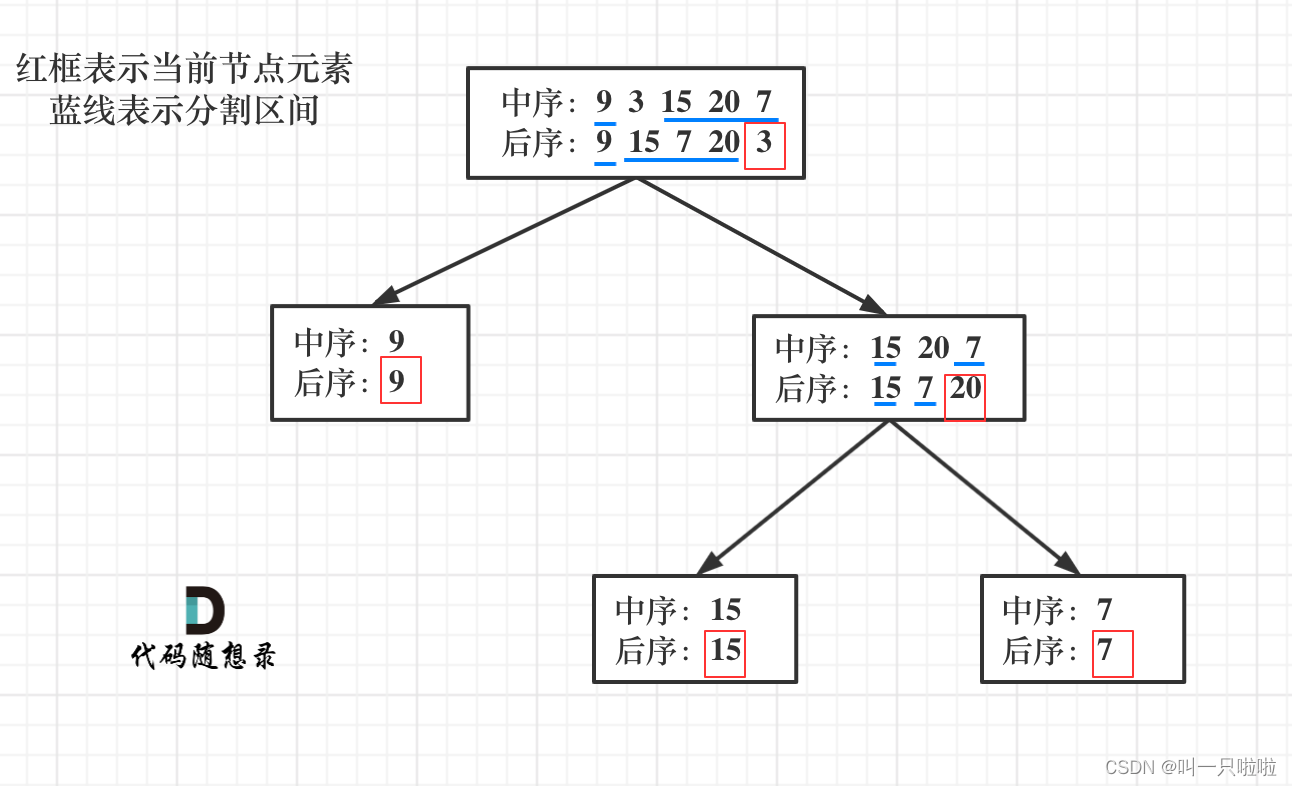
那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
其中,
难点就是如何切割,以及边界值找不好很容易乱套。
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
卡哥在数组:每次遇到二分法,都是一看就会,一写就废 (opens new window)和数组:这个循环可以转懵很多人! (opens new window)中都强调过循环不变量的重要性,在二分查找以及螺旋矩阵的求解中,坚持循环不变量非常重要,本题也是。
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右闭的原则:
整体代码如下
class Solution {
//存放中序遍历数组,方便之后快速查找 值 的索引位置
Map<Integer,Integer> map;
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i],i);
}
return structureTree(inorder,0, inorder.length-1,postorder,0, postorder.length-1);//左闭右闭
}
TreeNode structureTree(int[] inorder,int inorderStart,int inorderEnd, int[] postorder,int postorderStart,int postorderEnd){
//确定边界条件,左闭右闭
if (inorderStart > inorderEnd || postorderStart > postorderEnd){//如果不满足左闭右闭,说明没有元素,返回空
return null;
}
//获得根节点的值,创建节点
int val = postorder[postorderEnd];
//获得中序遍历中 值为 val 的索引
int index = map.get(val);
TreeNode node = new TreeNode(val);//构造节点
// 保存中序左子树的个数,用来确定后续数组的个数
int lenOfLeft = index - 1 - inorderStart;
//左
node.left = structureTree(inorder,inorderStart,index-1
,postorder,postorderStart,lenOfLeft + postorderStart);
//右
node.right = structureTree(inorder,index+1,inorder.length -1
,postorder,lenOfLeft + postorderStart + 1,postorderEnd - 1);
return node;
}
}以上为我做题时候的相关思路,自己的语言组织能力较弱,很多都是直接抄卡哥的,有错误望指正。