leetCode 1035.不相交的线动态规划 + 滚动数组（最长公共子序列）

news2024/11/26 4:51:57

1035. 不相交的线 - 力扣（LeetCode）

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

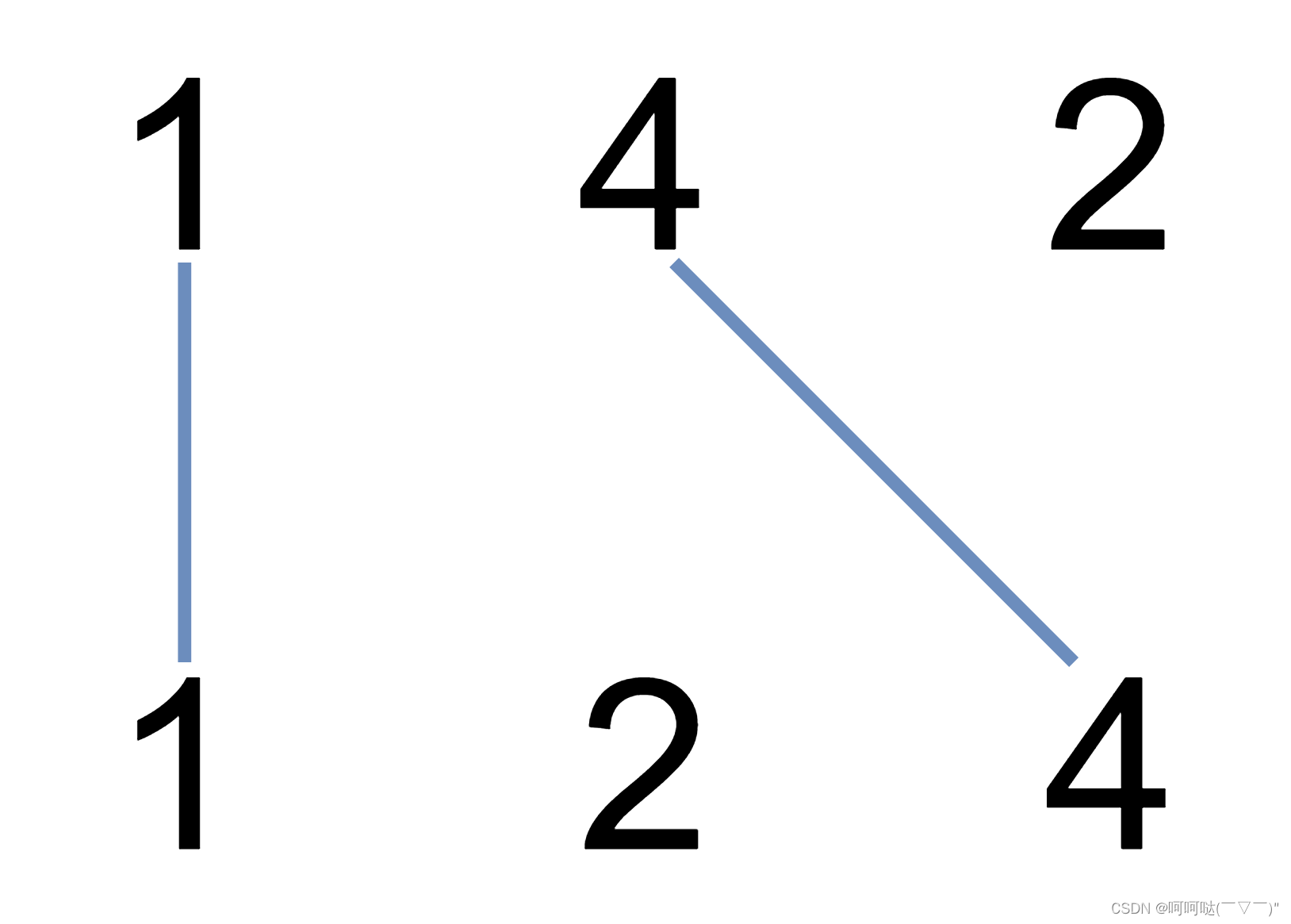
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

>>思路和分析

题目要求：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。

若思路是：找出两个数组中相同的元素，给它们连成线，还要保证这个线还不能相交，那如果就此深入思考，这个线如何判断它不能相交呢？就很容易陷进去了，很难相处解决的办法。

其实这里是找两个数组中相同的元素，同时其实要保证数组里边的元素的顺序，也就是求子序列问题。因为子序列也是在数组里边找元素的，但同时是保证数组里边的顺序。换言之，也就是说直线不能相交，这就是说明在nums1中找到一个与nums2相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

那问题就转换为找两个数组的相同子序列，且是最长公共子序列题目中的，相同元素要连成线，要避免线相交，又要让我们求出最多线的数量，其实都是壳子。也就是套了一个壳子的最长公共子序列。

本质：求最长公共子序列

注意：12和21不是相同的子序列

分析清楚之后，我们就知道本题说是求绘制的最大连接数，其实就是求两个字符串的最长公共子序列的长度，我的往期文章中：leetCode 1143.最长公共子序列和 leetCode 1143.最长公共子序列有详细求解最长公共子序列的长度的过程，感兴趣的读者可以看一下！

C++代码：

class Solution {
public:
    // 二维dp数组
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        for(int i=1;i<=nums1.size();i++) {
            for(int j=1;j<=nums2.size();j++) {
                if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

时间复杂度: O(n * m)，其中 n 和 m 分别为 nums1和 nums2的长度
空间复杂度: O(n * m)

>>优化空间复杂度：滚动数组

class Solution {
public:
    // 一维dp数组
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<int> dp(nums2.size()+1,0);
        int result = 0;
        for(int i=1;i<=nums1.size();i++) {
            int pre = dp[0];// 0
            for(int j=1;j<=nums2.size();j++) {
                int tmp = dp[j];
                if(nums1[i-1] == nums2[j-1]) dp[j] = pre + 1;
                else dp[j] = max(dp[j],dp[j-1]);
                pre = tmp;
            }
        }
        return dp[nums2.size()];
    }
};

时间复杂度: O(n * m)
空间复杂度: O(m)

参考和推荐文章、视频：

代码随想录 (programmercarl.com)https://programmercarl.com/1035.%E4%B8%8D%E7%9B%B8%E4%BA%A4%E7%9A%84%E7%BA%BF.html#%E6%80%9D%E8%B7%AF

动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1h84y1x7MP/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3

来自代码随想录的课堂截图：