且与或

含义

• A且B(A^B):同时存在
  • 常见形式
    • A并且B
    • 既A又B
    • 不但A而且B
    • 虽然A但是B
• A或B:二者至少有一个成立(即A且非B,非A且B,A且B)

否定形式

• 且的否定
  • A且B否定形式：非(A^B) = 非A 或 非B
  • 非A且非B否定形式：非(非A^非B) = A 或 B
  • 非A且B否定形式：非(非A^B) = A 或 非B
• 或的否定
  • A或B否定形式：非(A或B) = 非A ^ 非B
• 扩展
  • A且B且C否定形式：非(A^B^C) = 非A或非B或非C
  • A或B或C否定形式：非(A或B或C) = 非A^非B^非C

或的推理

推理前提：已知“A或B”为真

• 有效推理：否一推一
• 无效推理：肯定

补充考点

• 要么A要么B： A、B必然一真一假
• A或B对比

  

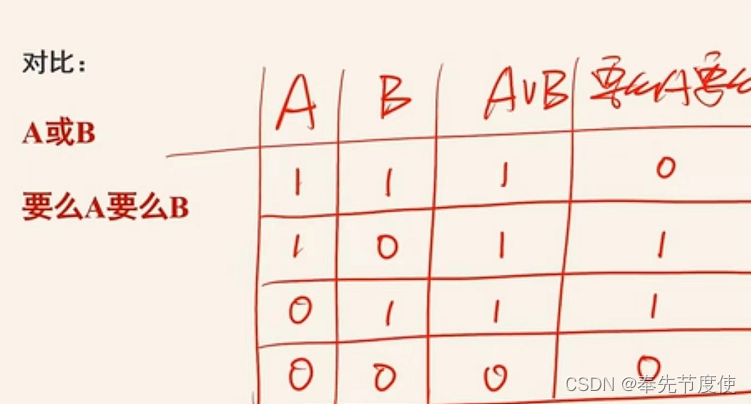
注意：只有A和B均为真时,A或B与要么A要么B结果不一致,其他情况均相同

充分条件(最重要的部分,涉及15道题左右)

含义

• 条件必然导致结果的发生,符号表示为A->B
• 常见形式
  • ​​​​​​​只要A,就B
  • 如果A,那么B
  • 若A,则B
  • 所有A是B
  • A必然B

否定形式

• A->B的否定：A真且B假(A^非B,即前真且后假)

推理规则

• 已知A->B,则推出非B->非A
  • 有效情况：即肯前必肯后,否后必否前
  • 无效情况：否前,肯后

补充考点(不怎么考~)

• 除非A,否则B
  • 符号表示即：非A->B
  • 注意
    • “否则”有时会省略,例如A,除非B,此时需要把否则补上后再判断,即否则A,除非B
    • “除非”本身力度较弱,和其他关系词配合时,以其他关系词为主
      • 若A,除非B：即可以理解为若A,则B, A->B
      • 除非A,才B：即可以理解为只要A,才B,B->A
• A->B的等价命题
  • A->B = 非A 或 B
  • 即前件为假(A真)或者后件为真(B真),则可以推出A->B恒真

必要条件

含义

• 只有A才B,后推前符号表示为B->A
• 常见形式
  • A是B的前提/必要条件

否定形式

• B->A​​​​​​​的否定：B真且A假(B^非A,即前真且后假)

推理规则

• 只有A,才B,即B->A,则可以推出非A->非B
  • 有效情况：肯前必肯后,否后必否前
  • 无效情况：否前,肯后

补充考点(不怎么考~)

• 充要条件
  • A既是B的充分条件,也是B的必要条件
  • 即符号可以表示为A<-->B
  • 否定形式：非A<-->非B

进阶技巧

无线索推理

• 题目特点：没有确定信息,难以入手
• 解题方法：做假设推出矛盾,则假设不成立

压轴题

• 画表格,找出对应(o表示)与不对应关系(x表示)​​​​​​​