【牛客面试必刷TOP101】Day9.BM37 二叉搜索树的最近公共祖先和BM42 用两个栈实现队列

news2024/11/23 19:30:07

作者简介：大家好，我是未央；

博客首页：未央.303

系列专栏：牛客面试必刷TOP101

每日一句：人的一生，可以有所作为的时机只有一次，那就是现在！！！！！

文章目录

前言

一、二叉搜索树的最近公共祖先

题目描述

解题分析

二、用两个栈实现队列

题目描述

解题分析

总结

前言

一、二叉搜索树的最近公共祖先

题目描述

描述：

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q，最近公共祖先LCA(T,p,q)表示一个节点x，满足x是p和q的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先.

2.二叉搜索树是若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值

3.所有节点的值都是唯一的。

4.p、q 为不同节点且均存在于给定的二叉搜索树中。

数据范围:

3<=节点总数<=10000

0<=节点值<=10000

举例说明：

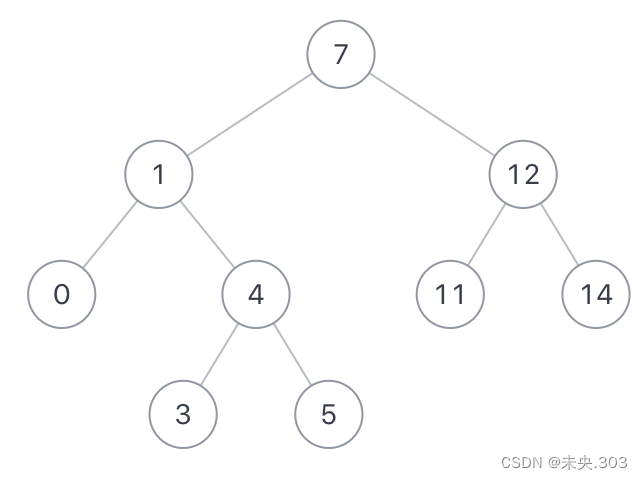
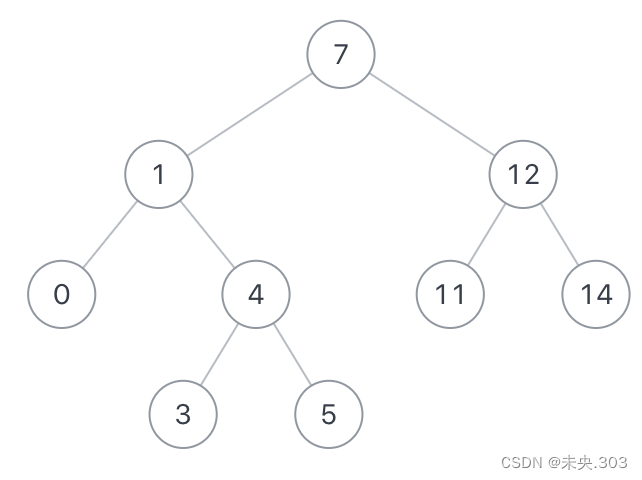
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5}，如下图:

示例1：

示例2：

解题分析

解题思路：
二叉搜索树的定义：

二叉搜索树是一种特殊的二叉树，它的每个节点值大于它的左子节点，且大于全部左子树的节点值，小于它右子节点，且小于全部右子树的节点值。因此二叉搜索树一定程度上算是一种排序结构。

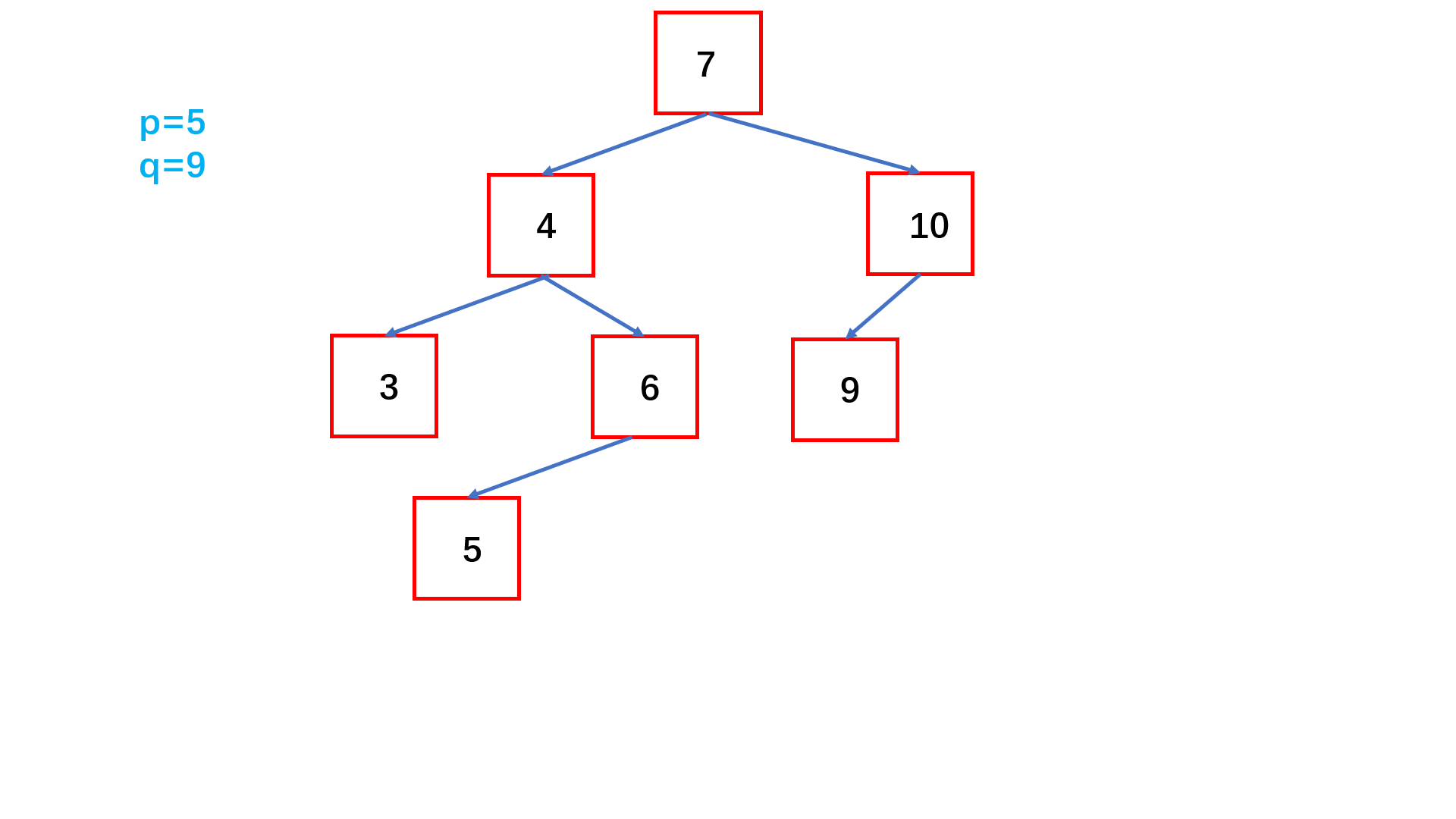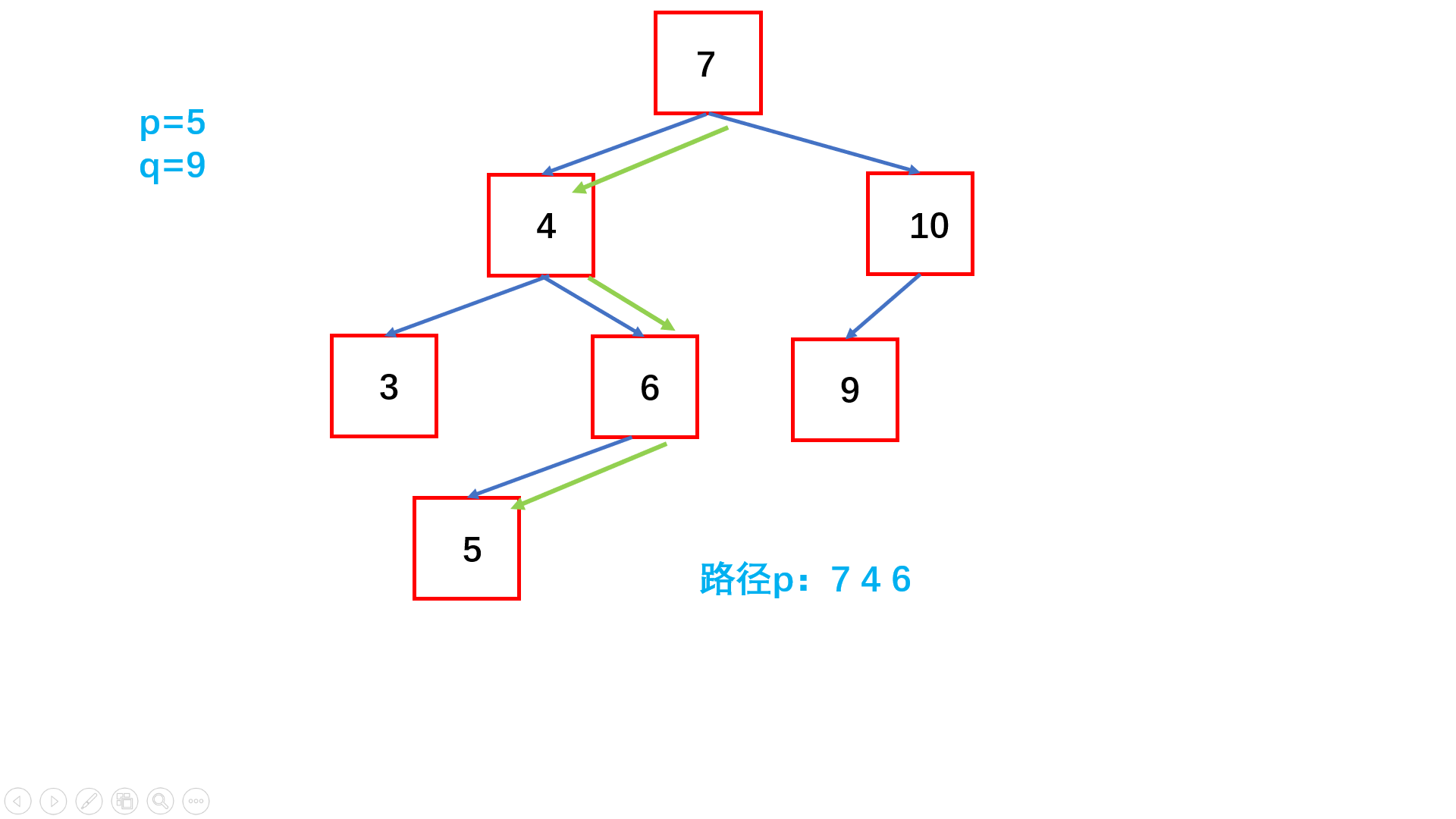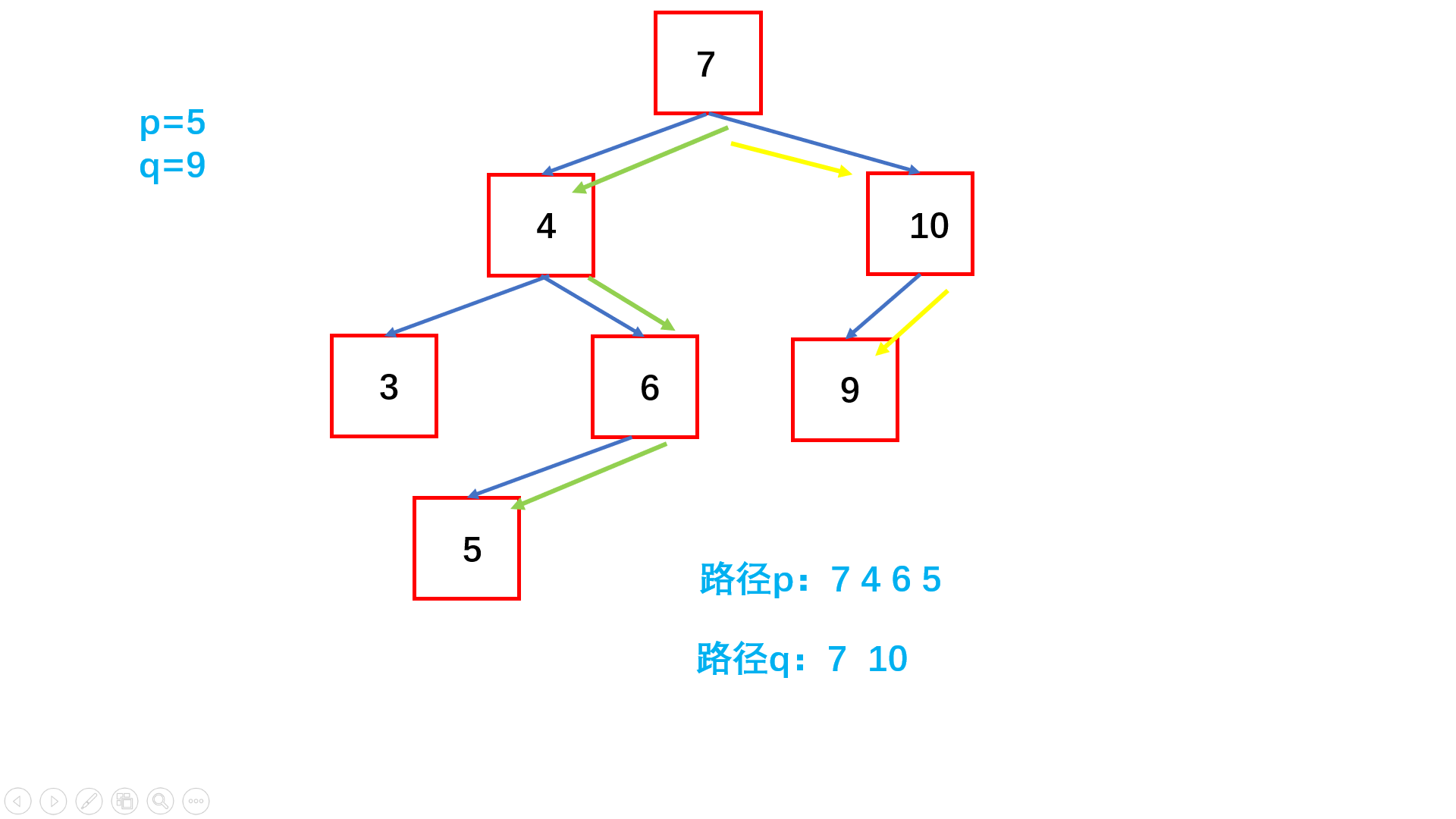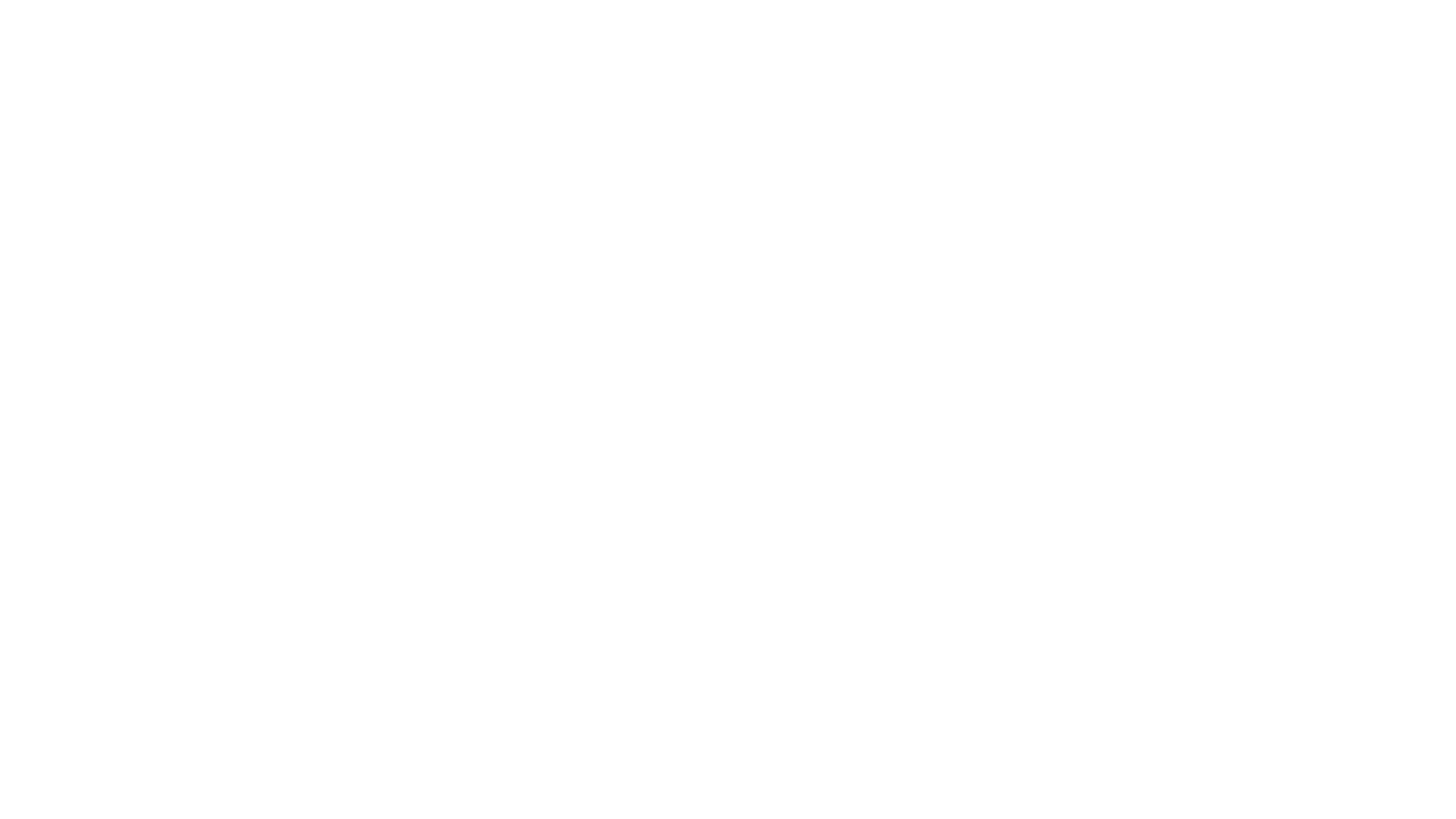
图示举例说明：

思路：

二叉搜索树没有相同值的节点，因此分别从根节点往下利用二叉搜索树较大的数在右子树，较小的数在左子树，可以轻松找到p、q；
//节点值都不同，可以直接用值比较
while(node.val != target) { 
    path.add(node.val);
    //小的在左子树
    if(target < node.val) 
        node = node.left;
    //大的在右子树
    else 
        node = node.right;
}
直接得到从根节点到两个目标节点的路径，这样我们利用路径比较就可以找到最近公共祖先。

解题步骤：

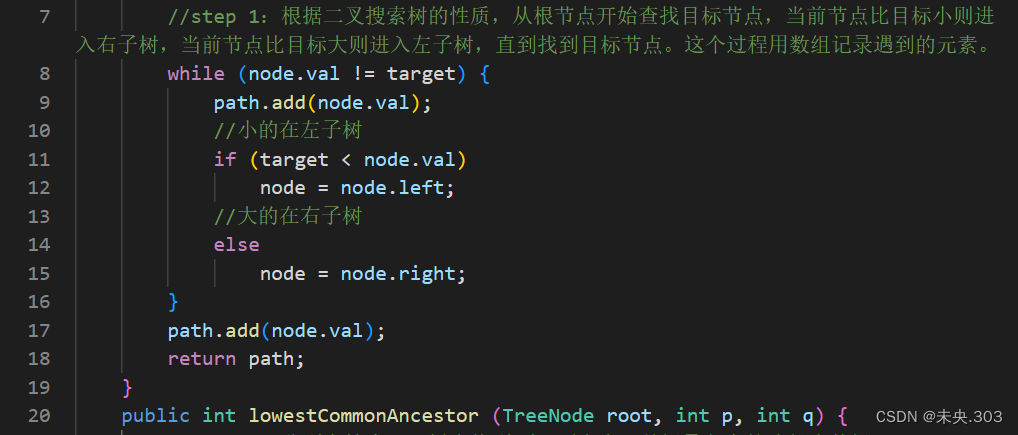
step 1：根据二叉搜索树的性质，从根节点开始查找目标节点，当前节点比目标小则进入右子树，当前节点比目标大则进入左子树，直到找到目标节点。这个过程用数组记录遇到的元素。
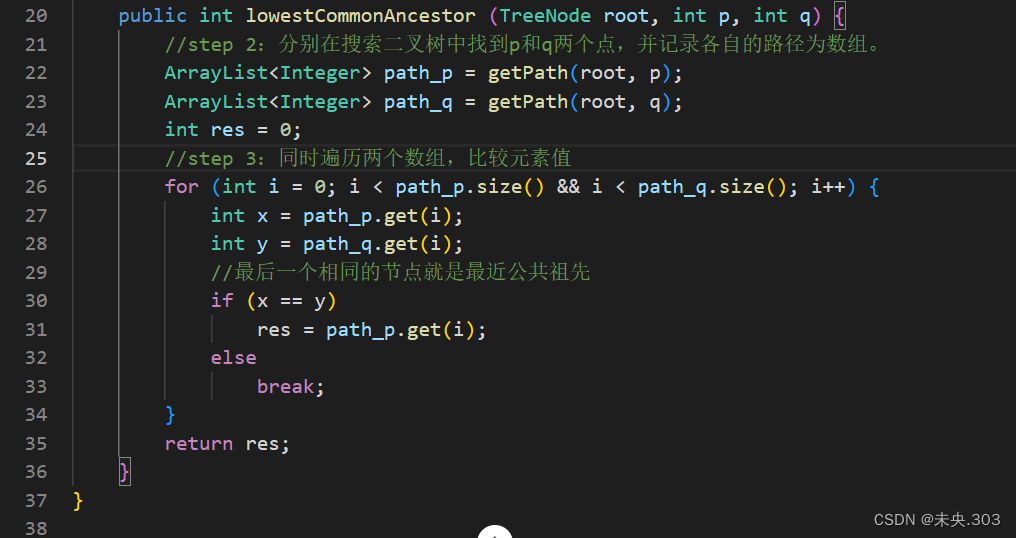
step 2：分别在搜索二叉树中找到p和q两个点，并记录各自的路径为数组。
step 3：同时遍历两个数组，比较元素值，最后一个相等的元素就是最近的公共祖先。

图示过程解析：

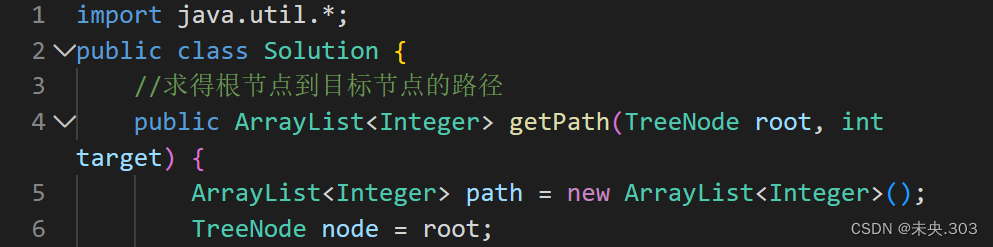
代码编写：

二、用两个栈实现队列

题目描述

描述：

用两个栈来实现一个队列，使用n个元素来完成 n 次在队列尾部插入整数(push)和n次在队列头部删除整数(pop)的功能。队列中的元素为int类型。保证操作合法，即保证pop操作时队列内已有元素。

数据范围：n≤1000；

要求：存储n个元素的空间复杂度为 O(n) ，插入与删除的时间复杂度都是 O(1)。

示例1：

示例2：

解题分析

解题思路：

双栈法（推荐使用）

思路：

元素进栈以后，只能优先弹出末尾元素，但是队列每次弹出的却是最先进去的元素，如果能够将栈中元素全部取出来，才能访问到最前面的元素，此时，可以用另一个栈来辅助取出。

解题步骤：
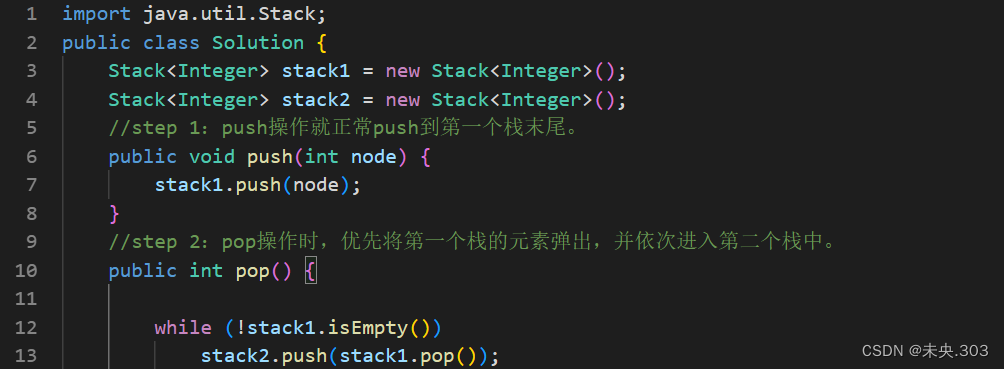
step 1：push操作就正常push到第一个栈末尾。
step 2：pop操作时，优先将第一个栈的元素弹出，并依次进入第二个栈中。
//将第一个栈中内容弹出放入第二个栈中
while(!stack1.isEmpty()) 
    stack2.push(stack1.pop()); 
step 3：第一个栈中最后取出的元素也就是最后进入第二个栈的元素就是队列首部元素，要弹出，此时在第二个栈中可以直接弹出。
step 4：再将第二个中保存的内容，依次弹出，依次进入第一个栈中，这样第一个栈中虽然取出了最里面的元素，但是顺序并没有变。
//再将第二个栈的元素放回第一个栈
while(!stack2.isEmpty()) 
    stack1.push(stack2.pop());
图示过程解析：