Stewart六自由度正解、逆解计算-C#和Matlab程序

news2024/11/25 4:29:19

目录

一、Stewart并联六自由度正解计算   

（一）概况     

（二）Matlab正解计算

1、参考程序一

2、参考程序二

（三）C#程序正解计算

1、工程下载链接

2、正解运行计算

（四）正程序打包下载程序合集

二、逆解计算

（一）Matlab逆解计算

1、Matlab逆解计算程序一

2、Matlab逆解计算程序二

3、Matlab逆解计算程序三

（二）C#程序逆解计算

1、工程下载链接

2、逆解运行计算

（三）逆解程序打包下载程序合集

一、Stewart并联六自由度正解计算   

（一）概况     

Stewart平台，也称为六自由度并联机构，是一种具有六个自由度（三个平移自由度和三个旋转自由度）的机械结构。它由一个固定的底座和一个可移动的平台组成，通过六个连杆连接底座和平台。

要进行Stewart平台的正解计算，即已知各个连杆的长度和底座上的固定点坐标，求解平台上的移动点坐标。正解计算可以通过以下步骤完成：

1. 定义底座和平台的坐标系。选择一个适当的坐标系，并将底座和平台的坐标系与之关联。

2. 确定底座上的固定点坐标。假设底座上有六个固定点，分别记作P1, P2, P3, P4, P5, P6，并给出它们在底座坐标系中的坐标。

3. 确定各个连杆的长度。假设有六个连杆，分别记作L1, L2, L3, L4, L5, L6，并给出它们的长度。

4. 确定平台上的移动点坐标。假设平台上有一个移动点M，并给出它在平台坐标系中的坐标。

5. 利用三角关系计算各个连杆的角度。根据已知的底座固定点坐标、连杆长度和平台上的移动点坐标，可以使用三角关系计算出各个连杆的角度。

6. 利用旋转矩阵计算平台的位姿。根据各个连杆的角度，可以构建旋转矩阵，然后将平台上的移动点坐标转换到底座坐标系中，从而得到平台的位姿。

以上步骤仅为大致的计算过程，具体实现时需要根据具体的连杆结构和坐标系选择进行适当的数学推导和计算。在实际应用中，还需要考虑误差校正、奇异姿态等问题。

请注意，Stewart平台的正解计算相对复杂，需要较强的数学和几何知识。如果你需要更详细和精确的计算结果，建议参考相关的文献或专业机器人学教材，或者使用专门的机器人仿真软件进行计算和分析。
 

（二）Matlab正解计算

1、参考程序一

      以下是一个使用MATLAB编写的Stewart并联六自由度正解计算的示例程序：

%这个程序计算了Stewart并联六自由度的正解，其中腿的长度 L 和腿的旋转角度 theta 是输入参数。
%程序通过循环计算每个腿的末端点坐标，并使用这些坐标计算平台的旋转矩阵。
%最后，程序打印出腿的末端点坐标和平台的旋转矩阵。
%你可以根据需要修改腿的长度和旋转角度，然后运行程序，即可得到相应的结果。

% 输入参数
L = [1, 1, 1, 1, 1, 1]; % 腿的长度
theta = [0, 0, 0, 0, 0, 0]; % 腿的旋转角度（单位：弧度）

% 计算腿的末端点坐标
P = zeros(3, 6); % 存储末端点坐标
for i = 1:6
    P(:, i) = [L(i)*cos(theta(i)); L(i)*sin(theta(i)); 0];
end

% 计算平台的旋转矩阵
R = zeros(3, 3); % 存储旋转矩阵
for i = 1:6
    R = R + cos(theta(i))*eye(3) + (1 - cos(theta(i)))*(P(:, i)*P(:, i)') - sin(theta(i))*skewSymmetricMatrix(P(:, i));
end

% 打印结果
disp("腿的末端点坐标：");
disp(P);
disp("平台的旋转矩阵：");
disp(R);

% 辅助函数：计算叉乘矩阵
function M = skewSymmetricMatrix(v)
    M = [  0    -v(3)   v(2);
           v(3)   0    -v(1);
          -v(2)  v(1)    0  ];
end

计算结果

2、参考程序二

% 输入参数
L = [0.5, 0.5, 0.5, 0.5, 0.5, 0.5]; % 腿的长度
theta = [pi/6, pi/4, pi/3, pi/6, pi/4, pi/3]; % 腿的旋转角度

% 计算腿的末端点坐标
P = zeros(3, 6); % 存储末端点坐标
for i = 1:6
    P(:, i) = [L(i)*cos(theta(i)); L(i)*sin(theta(i)); 0];
end

% 计算平台的旋转矩阵
R = zeros(3, 3); % 存储旋转矩阵
for i = 1:6
    R = R + cos(theta(i))*eye(3) + (1 - cos(theta(i)))*(P(:, i)*P(:, i)') - sin(theta(i))*skewSymmetricMatrix(P(:, i));
end

% 打印结果
disp("腿的末端点坐标：");
disp(P);
disp("平台的旋转矩阵：");
disp(R);

% 绘制图形
figure;
hold on;
grid on;
axis equal;
xlabel('X');
ylabel('Y');
zlabel('Z');

% 绘制腿的末端点
scatter3(P(1,:), P(2,:), P(3,:), 'filled');

% 绘制平台
platform = [0, 1, 1, 0, 0; 0, 0, 1, 1, 0; 0, 0, 0, 0, 0];
platform = R * platform;
patch(platform(1,:), platform(2,:), platform(3,:), 'r');

% 绘制连线
for i = 1:6
    line([0, P(1,i)], [0, P(2,i)], [0, P(3,i)], 'Color', 'b');
end

% 辅助函数：计算叉乘矩阵
function M = skewSymmetricMatrix(v)
    M = [  0    -v(3)   v(2);
           v(3)   0    -v(1);
          -v(2)  v(1)    0  ];
end

计算结果

（三）C#程序正解计算

1、工程下载链接

工程下载链接：

https://download.csdn.net/download/panjinliang066333/88421740

2、正解运行计算

给定下平台顶点坐标、六个连杆长度和角度，去计算旋转矩阵和位置矩阵。

以下是一个使用C#编写的Stewart并联六自由度正解计算的示例程序：

主运行程序

​

运行结果

​

在上述示例程序中，我们定义了底座上的固定点坐标、连杆长度和平台上的移动点坐标，并调用`StewartForwardKinematics`方法计算平台的位置坐标和姿态（旋转矩阵）。最后，我们将结果显示在控制台中。

请注意，这只是一个简化的示例程序，仅用于演示Stewart并联六自由度正解计算的基本思路。在实际应用中，可能需要考虑更多的细节和特殊情况，例如奇异姿态、误差校正等。如果需要更精确和完整的计算，建议参考相关的机器人学文献或专业软件。
 

（四）正程序打包下载程序合集

下载链接：

https://download.csdn.net/download/panjinliang066333/88421740

二、逆解计算

Stewart平台的逆解计算是指根据给定的目标位置和姿态，求解平台上各个执行器的长度和角度。逆解计算可以使用数值方法或解析方法进行。

（一）Matlab逆解计算

1、Matlab逆解计算程序一



%逆解计算

L1=0.5;
L2=0.5;
L3=0.5;
L4=0.5;
L5=0.5;
L6=0.5;

R11=4.3322;
R12=0.2105;
R13=-1.5;
R21=0.2105;
R22=4.4237;
R23=1.366;
R31=1.5;
R32=-1.36;
R33=4.1463;

P1=[0.433;0.25;0];
P2=[0.3536;0.3536;0];
P3=[0.2500;0.4330;0];
P4=[0.433;0.25;0];
P5=[0.3536;0.3536;0];
P6=[0.2500;0.4330;0];
% 输入参数
L = [L1, L2, L3, L4, L5, L6]; % 腿的长度
R = [R11, R12, R13; R21, R22, R23; R31, R32, R33]; % 平台的旋转矩阵
P = [P1, P2, P3, P4, P5, P6]; % 腿的末端点坐标


% 计算基座坐标系到平台坐标系的转换矩阵
T = [R, zeros(3,1); 0 0 0 1];

% 计算腿的旋转角度
theta = zeros(1, 6); % 存储腿的旋转角度
for i = 1:6
    % 计算腿的末端点在基座坐标系下的坐标
    P_base = T \ [P(:, i); 1];
    P_base = P_base(1:3);
    
    % 计算腿的旋转轴
    a = L(i) * R(:, 3);
    
    % 计算腿的末端点在基座坐标系下在旋转轴方向上的投影
    b = dot(P_base, a) * a;
    
    % 计算腿的末端点在基座坐标系下在旋转轴垂直方向上的投影
    c = P_base - b;
    
    % 计算腿的旋转角度
    theta(i) = atan2(norm(cross(a, c)), dot(a, c));
end

% 打印结果
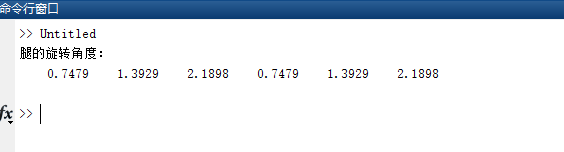
disp("腿的旋转角度：");
disp(theta);

% 辅助函数：计算叉乘矩阵
function M = skewSymmetricMatrix(v)
    M = [  0    -v(3)   v(2);
           v(3)   0    -v(1);
          -v(2)  v(1)    0  ];
end

在程序中，你需要提供腿的长度 L、平台的旋转矩阵 R 和腿的末端点坐标 P。程序首先计算基座坐标系到平台坐标系的转换矩阵 T，然后根据逆运动学的原理，计算每个腿的旋转角度 theta。

计算过程中，程序首先将腿的末端点坐标转换到基座坐标系下，然后计算腿的旋转轴和末端点在旋转轴方向上的投影。最后，根据旋转轴和投影的关系，计算腿的旋转角度。

请注意，这只是一个简单的示例程序，具体的实现可能会根据你的具体需求和机构的几何结构而有所不同。你可能需要根据你的应用场景进行适当的修改和扩展。

 运行结果

​

2、Matlab逆解计算程序二


%逆解计算

R11=4.3322;
R12=0.2105;
R13=-1.5;
R21=0.2105;
R22=4.4237;
R23=1.366;
R31=1.5;
R32=-1.36;
R33=4.1463;

P1=[0.433;0.25;0];
P2=[0.3536;0.3536;0];
P3=[0.2500;0.4330;0];
P4=[0.433;0.25;0];
P5=[0.3536;0.3536;0];
P6=[0.2500;0.4330;0];
% 输入参数
R = [R11, R12, R13; R21, R22, R23; R31, R32, R33]; % 平台的旋转矩阵
P = [P1, P2, P3, P4, P5, P6]; % 腿的末端点坐标

% 计算腿的长度
L = zeros(1, 6); % 存储腿的长度
for i = 1:6
    fprintf("计算第 %d 条腿的长度：\n", i);
    
    % 步骤1: 计算 a_i
    a = R(:, 3);
    fprintf("步骤1: a_%d = R(:, 3) =\n", i);
    disp(a);
    
    % 步骤2: 计算 b_i
    b = P(:, i);
    fprintf("步骤2: b_%d = P%d =\n", i, i);
    disp(b);
    
    % 步骤3: 计算 L_i
    L(i) = norm(b - a);
    fprintf("步骤3: L_%d = norm(b_%d - a_%d) = %.4f\n", i, i, i, L(i));
    
    fprintf("\n");
end

% 打印结果
disp("腿的长度：");
disp(L);

在程序中，你需要提供腿的长度 L、平台的旋转矩阵 R 和腿的末端点坐标 P。程序会按照步骤计算每个腿的长度，并给出每个步骤的中间结果。

请注意，这只是一个示例程序，具体的实现可能会根据你的具体需求和机构的几何结构而有所不同。你可以根据需要修改程序，添加额外的计算步骤或输出结果。

计算结果

​

3、Matlab逆解计算程序三


%逆解计算

R11=4.3322;
R12=0.2105;
R13=-1.5;
R21=0.2105;
R22=4.4237;
R23=1.366;
R31=1.5;
R32=-1.36;
R33=4.1463;

P1=[0.433;0.25;0];
P2=[0.3536;0.3536;0];
P3=[0.2500;0.4330;0];
P4=[0.433;0.25;0];
P5=[0.3536;0.3536;0];
P6=[0.2500;0.4330;0];
% 输入参数
R = [R11, R12, R13; R21, R22, R23; R31, R32, R33]; % 平台的旋转矩阵
P = [P1, P2, P3, P4, P5, P6]; % 腿的末端点坐标

% 计算腿的长度
L = zeros(1, 6); % 存储腿的长度
for i = 1:6
    fprintf("计算第 %d 条腿的长度：\n", i);
    
    % 步骤1: 计算 a_i
    a = R(:, 3);
    fprintf("步骤1: a_%d = R(:, 3) =\n", i);
    disp(a);
    
    % 步骤2: 计算 b_i
    b = P(:, i);
    fprintf("步骤2: b_%d = P%d =\n", i, i);
    disp(b);
    
    % 步骤3: 计算 L_i
    L(i) = norm(b - a);
    fprintf("步骤3: L_%d = norm(b_%d - a_%d) = %.4f\n", i, i, i, L(i));
    
    fprintf("\n");
end

% 打印结果
disp("腿的长度：");
disp(L);

在程序中，你需要提供腿的长度 L、平台的旋转矩阵 R 和腿的末端点坐标 P。程序会按照步骤计算每个腿的角度和长度，并给出每个步骤的中间结果。

请注意，这只是一个示例程序，具体的实现可能会根据你的具体需求和机构的几何结构而有所不同。你可以根据需要修改程序，添加额外的计算步骤或输出结果。

程序运行过程

​

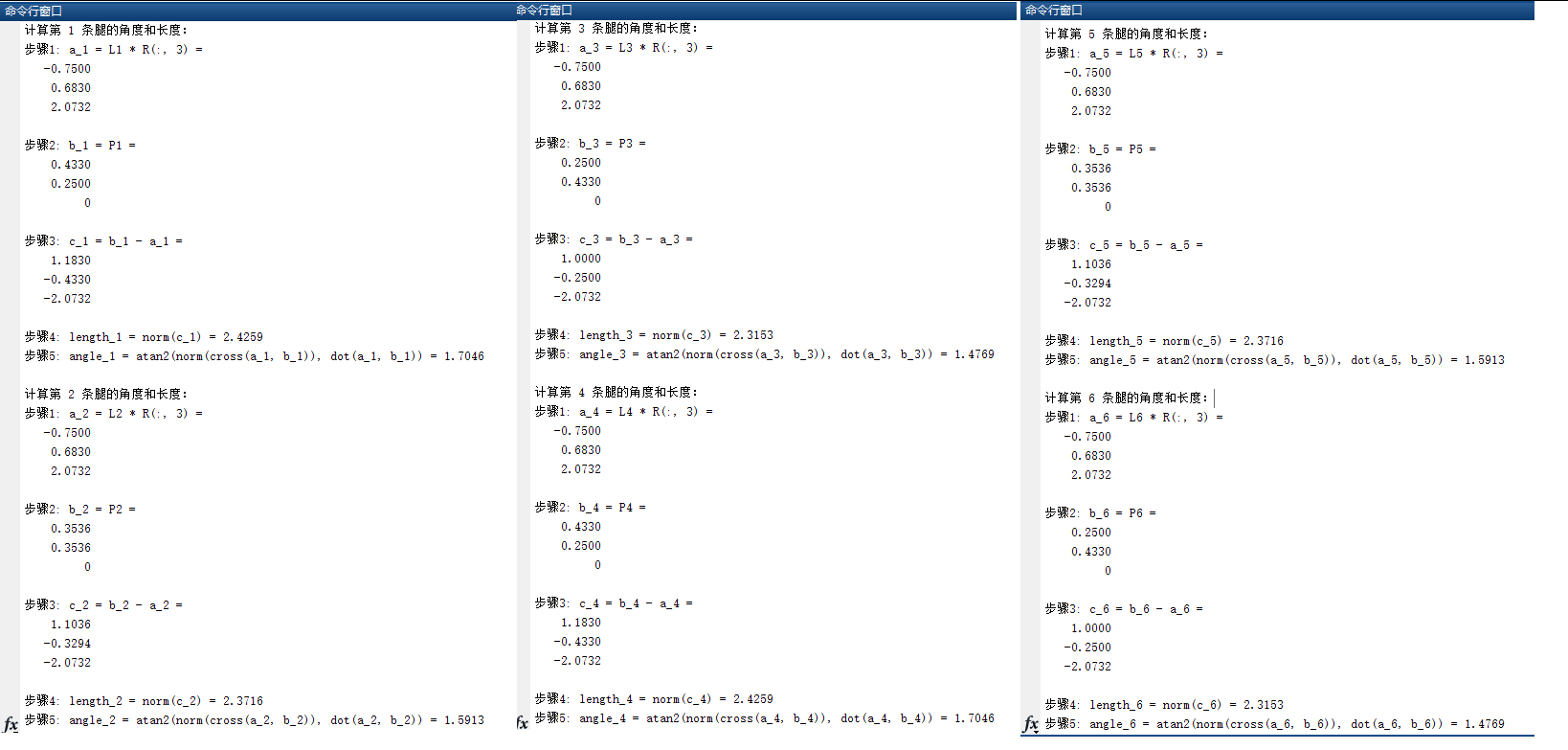
结果

​

（二）C#程序逆解计算

1、工程下载链接

工程下载链接：

https://download.csdn.net/download/panjinliang066333/88422020

2、逆解运行计算

给定下平台顶点坐标、六个连杆长度和角度，去计算旋转矩阵和位置矩阵。

以下是一个使用C#编写的Stewart并联六自由度正解计算的示例程序：

主运行程序

​

程序运行结果

​

（三）逆解程序打包下载程序合集

下载链接：

https://download.csdn.net/download/panjinliang066333/88422020

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1090776.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

zabbix监控——自定义监控内容

zabbix监控——自定义监控内容

目录 自定义监控项步骤 案例 1、明确需要执行的命令 2、创建 zabbix 的监控项配置文件，用于自定义 key，并重启zabbix-agent2 3、.在服务端验证新建的监控项 4、在 Web 页面创建自定义监控项模板 1）创建模板 2）创建监控项 …
阅读更多...
振弦传感器和无线振弦采集仪在隧道安全监测的解决方案

振弦传感器和无线振弦采集仪在隧道安全监测的解决方案

振弦传感器和无线振弦采集仪在隧道安全监测的解决方案 隧道作为交通工程的重要组成部分，具有极高的安全风险，因此隧道安全监测是必不可少的。振弦传感器和无线振弦采集仪作为隧道安全监测的两种重要设备，能够有效地监测隧道的振动情况&#…
阅读更多...
探索JSON能力，看这一篇就够了

探索JSON能力，看这一篇就够了

KING BASE JSON（JavaScript Object Notation）作为一种流行的数据格式，相比于TEXT和LOB类型，能更高效地实现数据的访问。此外，JSON能打通关系型和非关系型数据存储之间的界限，为业务提供更好的架构选择。 Ki…
阅读更多...
POI、Easy Excel操作Excel

POI、Easy Excel操作Excel

文章目录 1.常用的场景2.基本功能3.Excel在Java中是一个对象4. 简单的写（07版本（.xlsx）Excel）大文件写HSSF大文件写XSSF大文件写SXSSF 5. Excel读5.1 读取遇到类型转化问题该怎么解决5.2 遇到Excel公式怎么办 6. Easy Excel6.1简单…
阅读更多...
[Python]黑色背景白色块滑动视频

[Python]黑色背景白色块滑动视频

黑色背景白色块滑动视频，单帧效果如下： 配置参数 1920 1080 400 400 300 60 1920x1080.avi import numpy as np import cv2 as cv import os import syswidth 1920 height 1080 rect_szx 400 rect_szy 300 sz_y_init 400 fps 24width int(sys.a…
阅读更多...
如何使用ChatPPT生成PPT文档

如何使用ChatPPT生成PPT文档

简介 ChatPPT是一个基于人工智能的PPT生成工具，可以帮助用户快速生成高质量的PPT文档。ChatPPT使用自然语言处理技术，可以根据用户的指令生成PPT内容、设计和排版。 使用方法 ChatPPT提供了两种使用方式：在线体验版和Office插件版。 在线…
阅读更多...
pytest 之 pytest.ini配置文件

pytest 之 pytest.ini配置文件

前言：pytest.ini全局配置文件，是pytest单元测试框架的核心配置文件，pytest.ini 可以改变 pytest 的默认行为 一、配置规则 1、优先级 如pytest.ini有该参数值，在执行的时候，优先读取配置文件中的参数如没有&#xf…
阅读更多...
ADAS可视化系统，让自动驾驶更简单 -- 入门篇

ADAS可视化系统，让自动驾驶更简单 -- 入门篇

随着车载芯片的升级、技术的更新迭代，可视化ADAS逐渐变成汽车的标配走入大家的生活中，为大家的驾车出行带来切实的便捷。那么你了解HMI端ADAS的实现过程吗？作为ADAS可视化系统的入门篇，就跟大家聊一聊目前较常见的低消耗的一种ADA…
阅读更多...
Android---深入理解AQS和CAS原理

Android---深入理解AQS和CAS原理

AQS AQS 全称是 Abstract Queued Synchronizer，一般翻译为同步器。是一套实现多线程同步功能的框架，由 Doug Lea 操刀设计并开发实现的。AQS 在源码中被广泛使用，尤其是在 JUC（Java Util Concurrent）中，比…
阅读更多...
allure测试报告生成逻辑--解决在Jenkins里打开allure报告页面后空白显示无数据问题（以window环境为例）

allure测试报告生成逻辑--解决在Jenkins里打开allure报告页面后空白显示无数据问题（以window环境为例）

前言 相信大家在用Jenkins持续集成+ant自动构建+jmeter接口测试+pytest代码.xml文件转化+allure测试报告为一体的接口自动化测试构建过程中，都会遇到Jenkins里打开allure报告页面后空白显示无数据问题这一现象级问题，今天Darren洋就给大家分享一下如何讲讲allure测试报告生成…
阅读更多...
MySQL——源码安装教程

MySQL——源码安装教程

MySQL 一、MySQL的安装1、RPM2、二进制3、源码 二、源码安装方式三、安装过程1、上传源码包2、解压当前文件并安装更新依赖3、对MySQL进行编译安装 四、其他步骤 一、MySQL的安装 首先这里我来介绍下MySQL的几种安装方式： 一共三种，RPM安装包、二进制包…
阅读更多...
通过okhttp调用SSE流式接口，并将消息返回给客户端

通过okhttp调用SSE流式接口，并将消息返回给客户端

通过一个完整的java示例来演示如何通过okhttp来调用远程的sse流式接口 背景：我们有一个智能AI的聊天界面，需要调用三方厂商的大模型chat接口，返回答案（因为AI去理解并检索你的问题的时候这个是比较耗时的，这个时候客户…
阅读更多...
10-SRCNN-使用CNN实现超分辨成像

10-SRCNN-使用CNN实现超分辨成像

文章目录 utils_dataset.pymodel.pytrain.pyuse.py主要文件 utils_dataset.py 工具文件，主要用来制作dataset，便于加入dataloader，用于实现数据集的加载和并行读取 model.py 主要写入网络（模型） train.py 主要用于训练 use.py 加载训练好的模型，用于测试或使用 utils_dat…
阅读更多...
Spring实战 | Spring AOP核心秘笈之葵花宝典

Spring实战 | Spring AOP核心秘笈之葵花宝典

Spring实战系列文章： Spring实战 | Spring IOC不能说的秘密？ 国庆中秋特辑系列文章： 国庆中秋特辑（八）Spring Boot项目如何使用JPA 国庆中秋特辑（七）Java软件工程师常见20道编程面试题 国庆…
阅读更多...
IDEA的常用设置

IDEA的常用设置

【1】进入设置： 【2】设置主题： 【3】编辑区的字体变大或者变小： 【4】鼠标悬浮在代码上有提示： 【5】自动导包和优化多余的包： 手动导包：快捷键：altenter 自动导包和优化多余的包&#xf…
阅读更多...
计算机网络第2章-HTTP和Web协议（2）

计算机网络第2章-HTTP和Web协议（2）

Web和HTTP 一个新型应用即万维网（World Wide Web）Web。 HTTP概况 Web的应用层协议是超文本传输协议（HTPP），它是Web的核心。 HTTP由两个程序实现：一个用户程序和一个服务器程序。 Web页面（W…
阅读更多...
leetcode-518. 零钱兑换 II

leetcode-518. 零钱兑换 II

1. 题目 链接: 零钱兑换II 2. 解决方案1 #include <stdio.h> #include <stdlib.h>int change(int amount, int* coins, int coinsSize){int dp[amount1];//确定dp大小memset(dp, 0, sizeof(int) * (amount1));dp[0] 1;//初始化为0for(int i 0 ; i < coins…
阅读更多...
LED电子屏幕可以通过什么方式进行人屏互动

LED电子屏幕可以通过什么方式进行人屏互动

传统的LED大屏幕以单向传播的形式面向观众&#xff0c;不仅被动&#xff0c;而且逐渐缺乏动感和创新。随着LED显示技术的蓬勃发展&#xff0c;现在观众与LED电子大屏幕的方式越来越多。那么现阶段实现LED显示屏人屏互动的主要方式都有哪些呢&#xff1f;带你8分钟了解LED互动地…
阅读更多...
KASan介绍

KASan介绍

目录 概括介绍 配置说明 单独关闭读或写检查 操作使用 影响及注意事项 结果解读 使用注意 实现原理简介 KASAN原理 malloc原理 内容参考 概括介绍 KernelAddressSANitizer &#xff08;KASAN&#xff09; 是一个动态内存错误检测器。它提供了一个快速而全面的解决方…
阅读更多...
D课堂 | 如何设置域名解析？解析记录类型选哪个？

D课堂 | 如何设置域名解析？解析记录类型选哪个？

上回&#xff0c;D妹和各位小伙伴们介绍了DNS的作用和原理——《什么是DNS&#xff1f;DNS是怎么运作的&#xff1f;》&#xff0c;相信大家对DNS已经有了一定的认识。 DNS是互联网不可或缺的基础服务&#xff0c;核心作用是将域名翻译成计算机可读取的IP地址&#xff0c;也就是…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023