Codeforces Round 903 (Div. 3)ABCDE
目录
- A. Don't Try to Count
- 题目大意
- 思路
- 核心代码
- B. Three Threadlets
- 题目大意
- 思路
- 核心代码
- C. Perfect Square
- 题目大意
- 思路
- 核心代码
- D. Divide and Equalize
- 题目大意
- 思路
- 核心代码
- E. Block Sequence
- 题目大意
- 思路
- 核心代码
A. Don’t Try to Count
题目大意
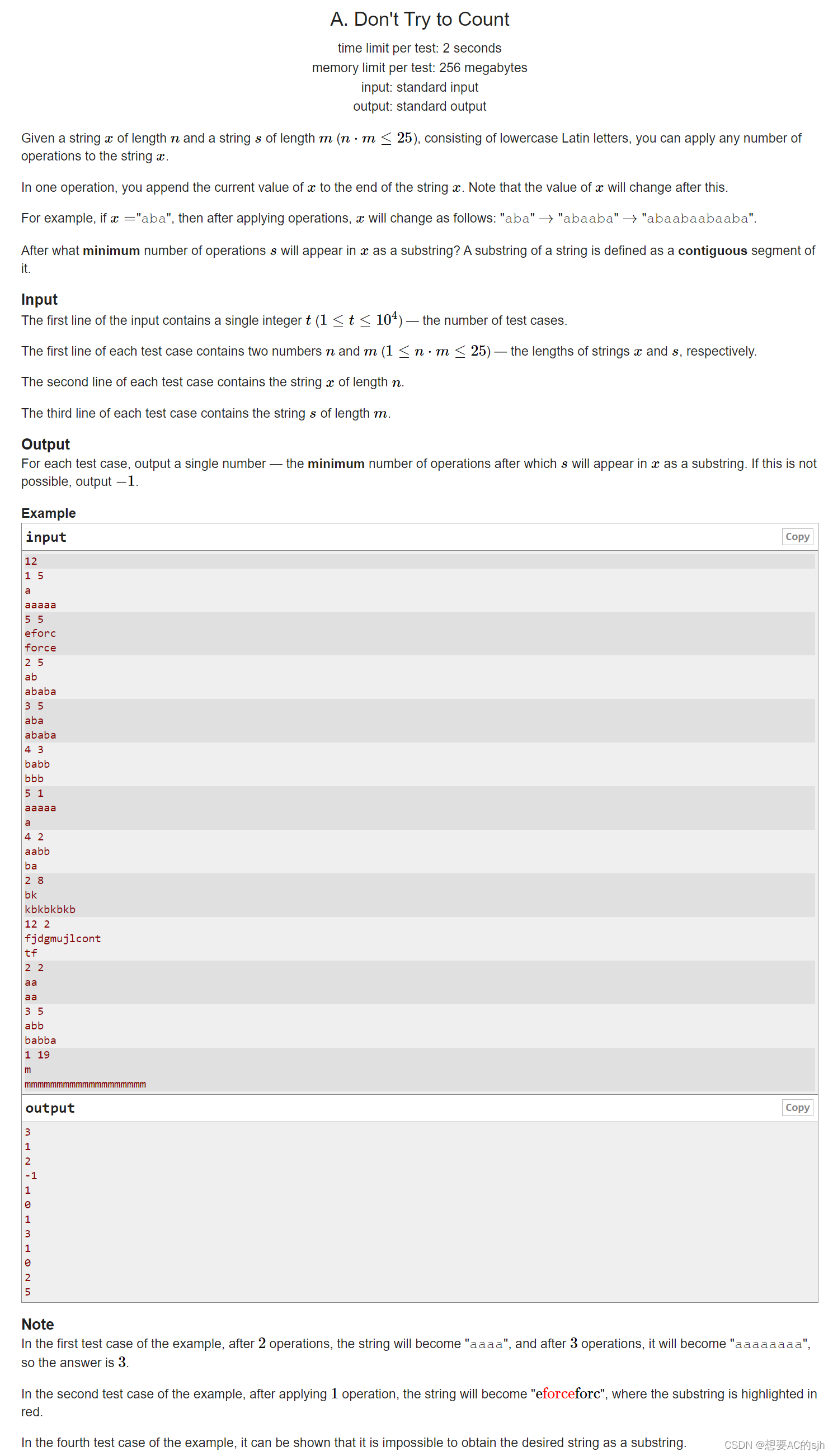
分别给你两个字符串 s s s和 x x x,可以对 x x x进行复制操作, x = x + x x=x+x x=x+x,如果可以通过这样的操作使得 s s s字符串成为字符串 x x x的子串,询问操作的次数
思路
首先,
s
s
s想要成为
x
x
x的子串,首先
x
x
x的长度要大于等于
s
s
s的长度。
其次,如果
x
x
x已经大于或等于
s
s
s的长度了,有可能会出现“abcdefg”和“gabcdef”的情况,此时我们需要再操作一次,后面无论再如何操作都无法达成题意
核心代码
void solve()
{
int n,m;
cin>>n>>m;
string s,p;
cin>>s>>p;
int cnt=0;
while(n<m)
{
s=s+s;
n<<=1;
cnt++;
}
for(int i=0;i<n;++i)
{
bool pd=1;
for(int j=i;j<i+m;++j)
{
if(s[j]!=p[j-i])
{
pd=0;
break;
}
}
if(pd)
{
cout<<cnt<<endl;
return ;
}
}
s=s+s;
n<<=1;
cnt++;
for(int i=0;i<n;++i)
{
bool pd=1;
for(int j=i;j<i+m;++j)
{
if(s[j]!=p[j-i])
{
pd=0;
break;
}
}
if(pd)
{
cout<<cnt<<endl;
return ;
}
}
cout<<-1<<endl;
}
B. Three Threadlets

题目大意
给你三个绳子长度,均为整数,每一次可以把一个绳子剪断成两个整数长度,最多减三次,询问这三个长度的绳子最后能否剪成所有的绳子长度相同
思路
最后长度相同,假设都为1,反过来进行两两相加操作可以得到能实现的比例,情况不多直接全部枚举就好,能实现的比例如下:

核心代码
void solve()
{
long long a,b,c;
cin>>a>>b>>c;
if(a>b)swap(a,b);
if(a>c)swap(a,c);
if(b>c)swap(b,c);
if(a*1==b*1&&b*4==c*1)cout<<"YES\n";
else if(a*2==b*1&&b*3==c*2)cout<<"YES\n";
else if(a*1==b*1&&b*1==c*1)cout<<"YES\n";
else if(a*1==b*1&&b*3==c*1)cout<<"YES\n";
else if(a*2==b*1&&b*1==c*1)cout<<"YES\n";
else if(a*1==b*1&&b*2==c*1)cout<<"YES\n";
else cout<<"NO\n";
}
C. Perfect Square
题目大意
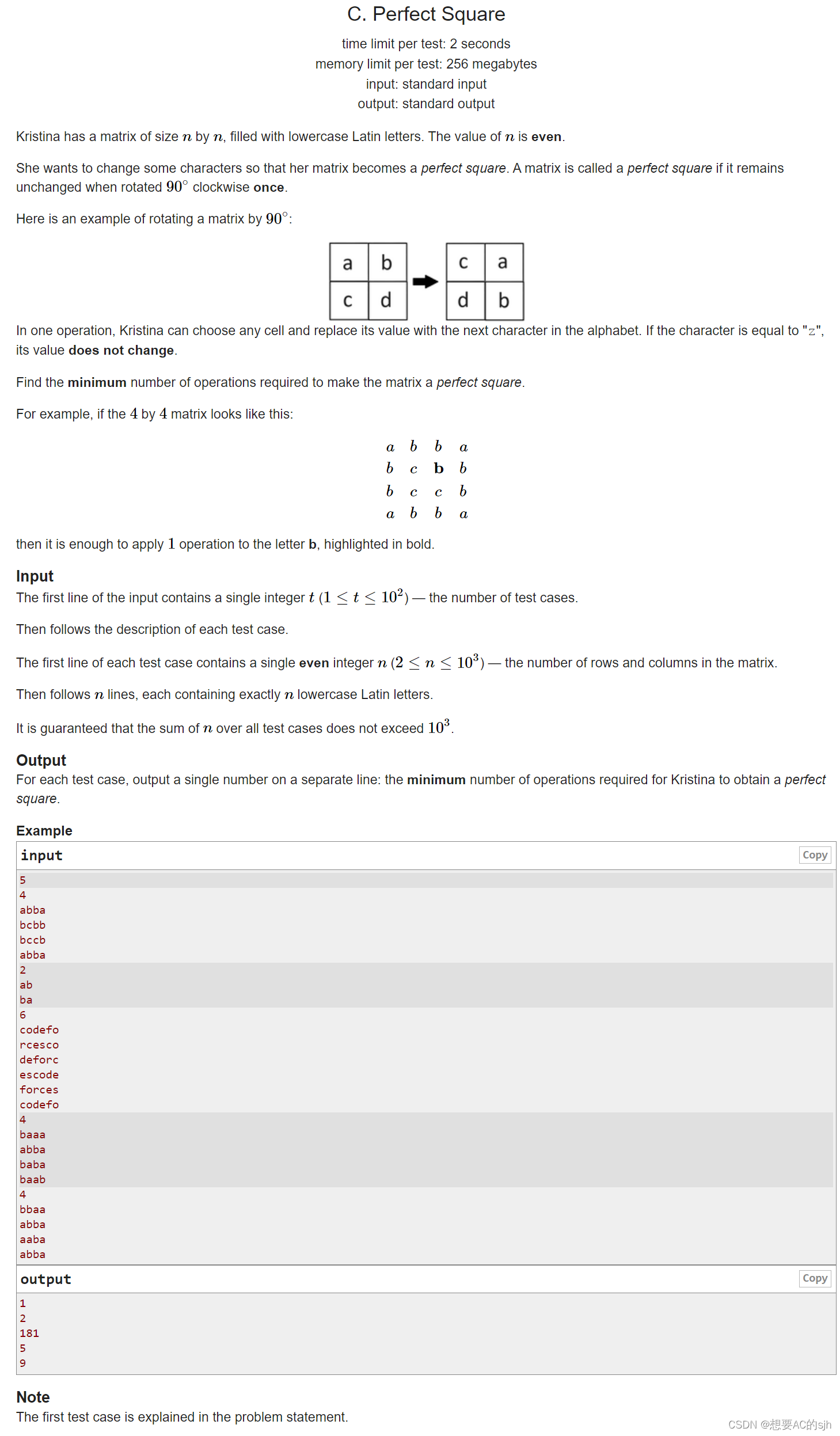
有一个边长为偶数n的正方形字母矩阵,每一次操作可以使得一个字母向后加一,“z”之后再加就不变了,现在想要把这个方阵变成顺时针旋转90°也能和原来一样的方阵,询问最少需要操作多少次
思路
旋转之后和原来一样,假设一个字母在左上角,则可以找到右上角、左下角、右下角都会有一个对应的点,这四个点的值应该是一样的,也就是我们需要把这对应的四个点都操作为原本这四个点中的最大值,对于左上角的所有点都这样找对应关系、求操作次数即可
核心代码
void solve()
{
int n;
cin>>n;
string s[1010];
{
for(int i=0;i<n;++i)
cin>>s[i];
}
long long ans=0;
for(int i=0;i<n/2;++i)
{
for(int j=0;j<n/2;++j)
{
int maxzhi=max(s[i][j],max(s[j][n-i-1],max(s[n-j-1][i],s[n-i-1][n-j-1])));
ans+=maxzhi*4-s[i][j]-s[n-1-i][j]-s[i][n-1-j]-s[n-1-i][n-1-j];
}
}
cout<<ans<<endl;
}
D. Divide and Equalize

题目大意
给你一个长度为 n n n的数组,每一次选取两个不同位置的数,可以把其中一个数除以它的因数,再把这个因数乘给另一个数,换句话说转化前后这两个数的乘积不变,询问最后这一个数组是否能转化为每一个数都一样
思路
最后每一个数都一样,说明所有的数的乘积后分解质因数,每一个质因数的个数都是 n n n的倍数,所以对于每一个数分解质因数最后统计每一个质因数的个数最后判断是否是 n n n的倍数即可得出答案
核心代码
int primes[N], cnt;
bool st[N];
void init(int n)
{
memset(st, 0, sizeof st);
cnt = 0;
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] * i < n; j ++ )
{
st[i * primes[j]] = true;
if (i % primes[j] == 0) break;
}
}
}
int zhuanghua(int a)
{
int left=0,right=cnt;
while(left<right)
{
int mid=left+((right-left)/2);
if(primes[mid]>a)right=mid;
else if(primes[mid]==a)return mid;
else left=mid+1;
//debug(mid);
}
return left;
}
int arr[1000000];
void solve()
{
int n;
cin>>n;
memset(arr, 0, 1000000);
for(int i=0;i<n;++i)
{
int x;
scanf("%d",&x);
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
arr[zhuanghua(i)]+=s;
}
if (x > 1) arr[zhuanghua(x)]++;
}
for(int i=0;i<cnt;++i)
{
if(arr[i]%n!=0) {
cout << "NO\n";
return;
}
}
cout<<"YES\n";
return ;
}
int main()
{
int t=1;
cin>>t;
init(1000000);
//cout<<zhuanghua(2);
while(t--)
{
solve();
}
return 0;
}
E. Block Sequence

题目大意
给定一个长度n整数序列,如果一个序列具有一系列块的形式,则称为美丽,每个块都从其长度开始,即首先是块的长度,然后是其元素。在一个操作中,可以从序列中删除任何元素。使给定序列美观所需的最小操作数是多少?
思路
使用动态规划的思想,假设dp[i]为第i的位置前面所有的数字想要成为美丽序列需要几次操作
一共有两种操作,第一种是移除第i位来实现,此时需要操作的次数为dp[i-1]+1
第二种是前面有一个完整的美丽块来实现,这种只能通过前面来推出后面,假设选中第i位为开头,那么后面第
i
+
a
i
+
1
i+ai+1
i+ai+1位以前想要成为美丽序列所需要的操作就是
d
p
[
i
+
a
i
+
1
]
=
d
p
[
i
]
dp[i+ai+1]=dp[i]
dp[i+ai+1]=dp[i]
以上两种情况保留最小值
核心代码
void solve()
{
int n;
cin>>n;
int arr[200005]{};
int dp[200005]{};
for(int i=1;i<=n;++i)
{
scanf("%d",&arr[i]);
dp[i]=INT_MAX;
}
dp[n+1]=INT_MAX;
dp[0]=-1;
for(int i=1;i<=n+1;++i)
{
dp[i]=min(dp[i-1]+1,dp[i]);
if(i+arr[i]+1<=n+1)dp[i+arr[i]+1]=min(dp[i],dp[i+arr[i]+1]);
}
cout<<dp[n+1]<<endl;
}