面试常考数据结构：红黑树、B树、B+树各自适用的场景

1. 磁盘基础知识

分页：

现代操作系统都使用虚拟内存来印射到物理内存，内存大小有限且价格昂贵，所以数据的持久化是在磁盘上。虚拟内存、物理内存、磁盘都使用页作为内存读取的最小单位。一般一页为4KB（8个扇区，每个扇区512B，8*512B=4KB）。

局部性原理：

当一个数据被用到时，其附近的数据也通常会马上被使用。
程序运行期间所需要的数据通常比较集中。

磁盘预读原理：

磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，这三个部分耗时相加就是一次磁盘IO的时间，大概 9ms 左右。这个成本是访问内存的十万倍左右；

磁盘读取的速度远小于内存，所以尽量减少 I/O 次数是提高效率的关键。

根据局部性原理，且由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），所以即使只需要读取一个字节，磁盘也会读取一页的数据。即磁盘预读时通常会读取页的整倍数。

2. 树基础知识回顾

排序二叉树：左 < 跟 < 右 B 树：有序数组 + 多叉平衡树，节点存储关键字、数据、指针； B+ 树：有序数组链表 + 多叉平衡树，非叶子节点存储指针、关键字，不存储数据；红黑树：红黑树是一种不大严格的平衡树（平衡树要求太高）

平衡树是为了防止二叉查找树退化为链表，而红黑树在维持平衡以确保 O(log2(n)) 的同时，不需要频繁着调整树的结构；

二叉树的存储结构

顺序存储（适用于完全二叉树）

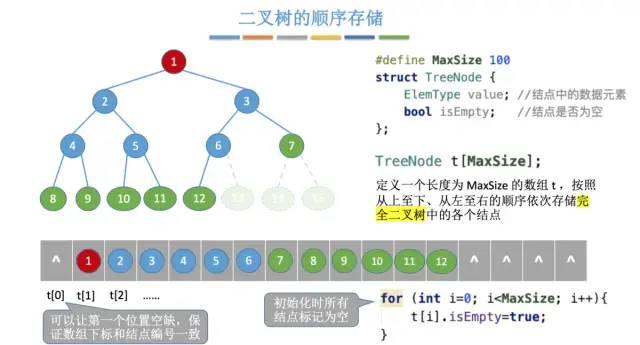
index 之间的对应关系：

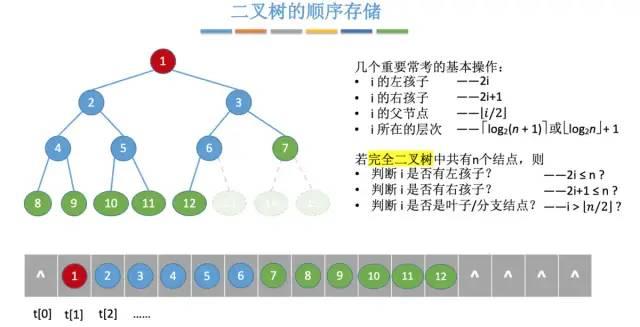
注意：二叉树的顺序存储只适合存储完全二叉树，否则 index 无法和节点对应起来，会有点恶心：

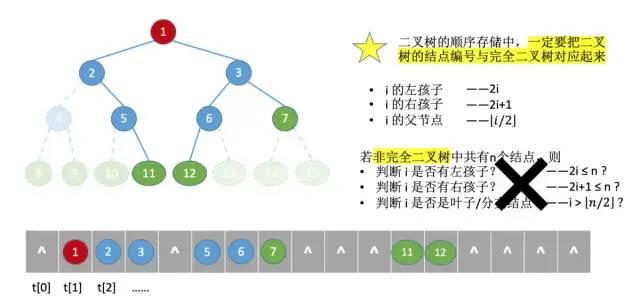
链式存储

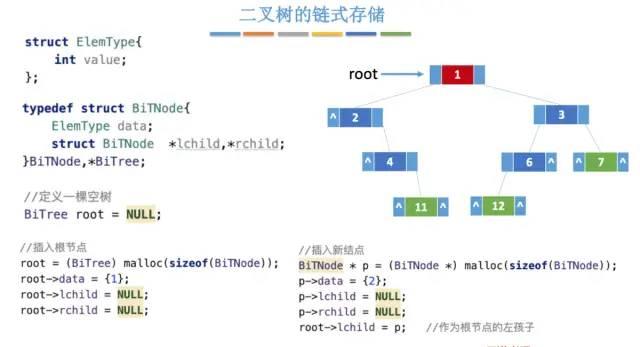
这里要好好理解一下，不然会影响后面的理解。

3. 为什么不能使用二叉树来存储数据库索引

先说结论：

平衡二叉树进行插入/删除时，大概率需要通过左旋/右旋来维持平衡；
旋转需要加载整个树，频繁旋转效率低；
二叉树的 I/O 次数近似为 O(log2(n))；
范围查询时，二叉树的时间复杂度会退化成 O(n)；
二叉树退化成链表时，时间复杂度也近似退化成了 O(n)；
二叉树无法使用磁盘预读功能；

其实单论范围查询，在关系型数据库中就基本没有使用二叉树的可能了。但是为了加深对知识的了解，来看看其他的原因。

先剔除掉范围查询的情况，原因 1、2、6 可以通过红黑树来解决，那么其实就剩下 2 个原因：

I/O 次数对比；
磁盘预读功能的利用；

4. 二叉树的 I/O 次数分析

先说 I/O 次数：

其实相比于二叉树，B 树、B+树， CPU 的运算次数并没有变化，甚至增多。但是 CPU 运算次数相比于 I/O 的消耗而言，可以忽略不计，所以 I/O 次数是评价一个数据库索引的效率高低的关键指标。

对于红黑树而言，其 I/O 次数近似为 log2(n)，为什么是近似呢？

首先，索引是存储在磁盘上的，磁盘上的数据大部分情况下是连续的，但是随着增删改查的发生，有可能产生很多碎片，也就是说：

索引在磁盘上的存储也不一定是连续的；

这里，严谨起见，我们来分两种情况：

索引节点，即树的节点在磁盘上存储是连续；

假设一个页能存储 5 个节点，假设二叉树如下：

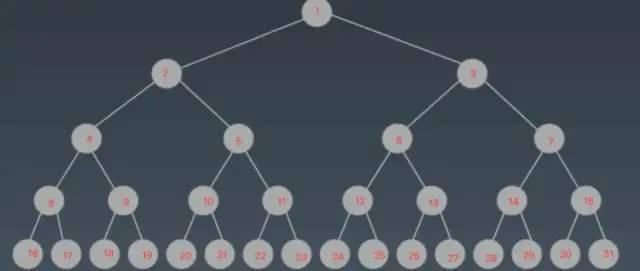
注意，序号只代表在磁盘中存储的顺序，不代表对应节点的关键字的值；

二叉树可能是链式存储，也可能是顺序存储。但是这里假设节点在磁盘上的存储是连续的，所以这里可以近似理解成顺序存储。即使是链式存储，无非就是 pNext 指针指向下一个连续的内存地址而已。

现在假设搜索的结果是最左边的叶子节点 16，因为磁盘预读的特性，加上一个页能存储 5 个节点，第一次 I/O ：

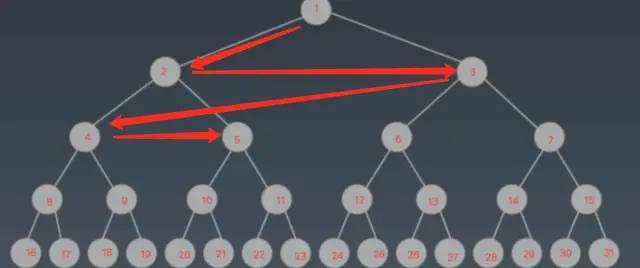
添加图片注释，不超过 140 字（可选）

如上，第一次 I/O 就读取了 5 个节点，不仅把根节点读取进内存了，还把节点 2 和 4 都读取进去了，看上去还节约了两次 I/O ？好厉害的样子……

此时，会根据二分法查找，对比 1 号节点然后去找节点 2，紧接着找节点 4，因为这两个节点都在内存中了，所以不需要进行 I/O

这里再说一次，序号不代表节点的关键字，而是单纯的表示节点在磁盘中的排列顺序；

紧接着，会需要 8 号节点，而 8 不再内存中，所以进行第二次 I/O 同样是读取一页，即 5 个节点：

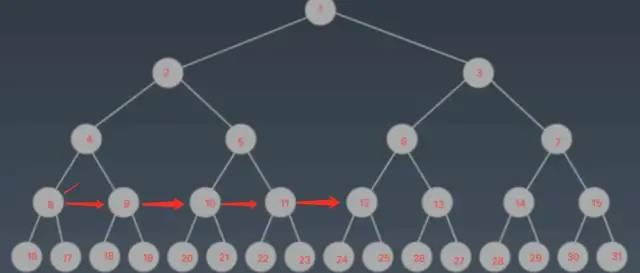
这次虽然也是读取了 5 个节点，但是实际上只有 8 号节点有实际作用，其他节点并没什么卵用（这是二叉树无法使用预读功能的本质），但是现在还没体现出劣势，现在对比之后需要 16 号节点，继续第三次读取：

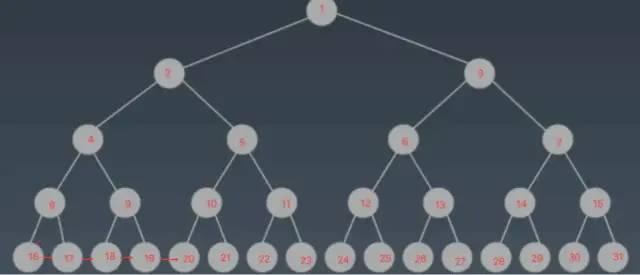
此时找到了 16，并将结果返回。

这是高度为 4 的情况，且只有 31 个数据。但是实际使用中，怎么可能就 31 个数据？假设要找的是 32 号节点，因为 16 号节点之后的 17-20 虽然被加载进内存了，但是完全没用。那么就需要再进行一次 I/O 来加载 32 号节点所在的页，同时也会将 33-36 加载进内存，但是这些节点并无卵用。

如果要找的是 1000 ，10000？

所以，随着层级的深入，会出现：

一个页中只有一个节点有用（二分法查找要的是子节点而不是兄弟节点）；
I/O 次数近似等于log2(n)；

即：

第一次 I/O 可能的优势在层级加深之后就没有了；
就算是红黑树，也只能将时间复杂度维持在 log2(n)；

上述讨论的是索引树在磁盘上的存储是连续的，如果不是连续的，那么按页读取到的脏数据会更多，上述的情况中，前几次 I/O 读取到有用的数据的概率会变低，所以 I/O 的次数只会增多而不会减少,即仍然是近似于 log2(n)。

5. B/B+树

B 树即：多路平衡查找树；

B 树的巧妙之处在于：

将一个节点的大小设置为一页的大小；
一个节点可以存放多个关键字（多叉树）；
自平衡；

这 3 点结合起来就可以做到：

一个节点大小为一页，被加载进内存时，这些关键字在进行对比，找出需要 leftChild 还是 rightChild 时，都是有用的（如最右侧时需要对比所有节点）；
一个节点可以存储多个关键字，有效降低了树的高度；

B+ 树的巧妙之处在于：

非叶子节点不存储数据，进一步增大了一页中存储关键字的数量；
叶子节点中存储数据且存在指向下一页的链表指针，可以使用顺序查询（支持范围查询）；

6. B/B+树的索引数量

B 树的节点中存储：指针、关键字(主键)、数据 B+ 树的非叶子节点：指针、关键字 B+树的叶子节点：指针(链表)、关键字、数据

注意，这里不是绝对的，比如有的 B+ 树中叶子节点存储的不是数据，而是指向数据的指针。查询到指针之后再去对应地址取出数据，但是这样应该会增加一次 I/O 吧，应该也是在数据量和 I/O 次数之间做了取舍，具体先不讨论。

以 Sqlite3.12 之后为例，page_size = 16k，假设指针为 8 byte，假设关键字类型占 8 byte，假设数据占 1 KB；

B 树的一个节点：

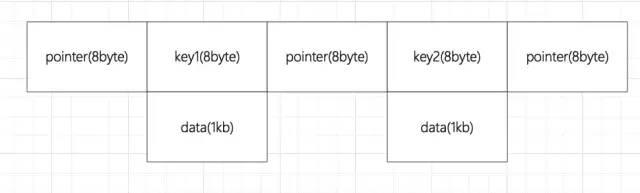
一页能存储的数据量为：16kb / (1KB+8byte+8byte) ≈ 16；

高度为 3 的 B 树能存储 16 x16 x16 = 4096 条数据

相比于二叉树的 1 个而言，确实有效降低了树的层级。而且上述是假设数据为 1KB，如果数据没那么大，高度为 3 的 B 树能存储更多的数据，但是如果用在大型数据库索引上还是不够。

B+ 树：

如上图，B+树的核心在于非叶子节点不存储数据。

这样做可以减少非叶子结点占用的空间，增大一页所能存储的数据量，最大程度减少树的层级。

仍然是以上假设，假如树的高度为 3 ，那么就有两层存储关键字+指针，一层叶子节点来存储实际数据。

一页能存储的关键字为：16 * 1024 / (8 + 8) = 1024 一页能存储的数据量为：16KB / (1KB + 8byte + 8byte) = 16 （这里计算不完全准确，实际情况应该是1页数据中只有一个链表指针指向下一页）能存储的关键字为：1024 * 1024 = 1048576；

因为端节点又有 1024 个指针，这些指针可以指向一个页，页中存储数据，也就是叶子节点，一页能存储 16 个叶子节点，所以总共能索引的数据量为 1048576 * 16 ≈ 1600万；如果高度为 4 ，则再乘以 1024 约为 17亿…..

上述推理中，理解终端节点的指针指向一个页，页中存储着关键字 + 数据 + 链表指针是关键。page 标记如下，有助理解：

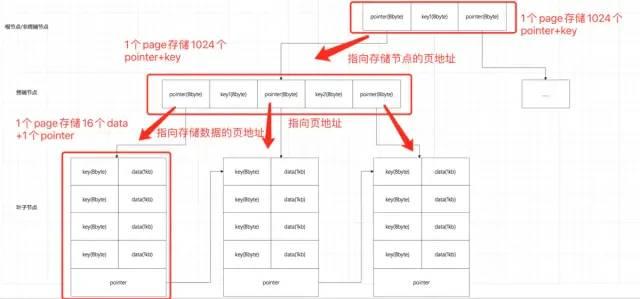
虽然叶子节点很多，一个 page 对应一个叶子节点甚至是多个 page 才能存下一个叶子节点，但是这些是存在磁盘上的，找到对应的 page 之后才去加载对应的 page。索引超大数据量的同时，不会对 I/O 次数产生影响，这就是这个设计的牛逼之处。

但是这样也是有缺点的：

无论查询结果如何，都必须走到叶子节点才结束，也就是 I/O 次数固定为 O(h) 或者说是 log(n)（底数为节点子分支个数），这个 h 一般为 2-3，排除掉根节点常驻内存，高度为 3 的 B+ 树进行两次 I/O 就可以索引千万级别的数据,高度为 4 的 B+ 树，进行 3 次 I/O 就能索引十亿级别的数据量，这个效果还是很好的。

所以，这个缺点也可以说成是优点：稳定（稳如一条老狗🐶）