https://vjudge.net/contest/587311#problem/C

最近没打这个套路，场上忘了

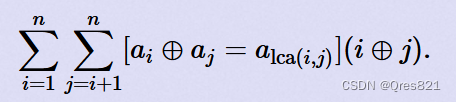
发现和一堆lca什么的有关，然后又是lca下不同的儿子，考虑树上启发式合并。

对于 $i\oplus j$，我们可以拆位枚举

然后常数大会被卡常。但树上启发式合并很多的dfs可以优化成遍历dfs序上一段连续的区间。

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
//#define mo
#define N 100010
int n, m, i, j, k, T;
int ans, son[N], w[N], a[N], c[N], p[N], u, v, sum;
int dfn[N], L[N], R[N], tot; 
vector<int>G[N]; 
int s[2][N*20]; 

void dfs1(int x, int fa) {
	w[x]=1; dfn[++tot]=x; 
	L[x]=tot; 
	for(int y : G[x]) {
		if(y==fa) continue; 
		dfs1(y, x); 
		w[x]+=w[y]; 
		if(w[y]>w[son[x]]) son[x]=y; 
	}
	R[x]=tot; 
}

//void dfs_clear(int x, int fa) {
//	
//	for(int y : G[x]) 
//		if(y != fa) dfs_clear(y, x); 
//}

//void dfs3(int x, int fa, int k) {
	printf("%lld : %lld => %lld | %lld\n", x, c[x], c[x]^k, s[a[x]^1][c[x]^k]); 
//	ans += s[a[x]^1][c[x]^k]; 
//	for(int y : G[x]) 
//		if(y != fa) dfs3(y, x, k); 
//}
//
//void dfs4(int x, int fa) {
//	s[a[x]][c[x]] ++ ; 
//	for(int y : G[x]) if(y != fa) dfs4(y, x); 
//}

void dfs2(int x, int fa) {
	int p; 
	for(int y : G[x]) if(y != fa && y != son[x]) {
		dfs2(y, x); 
		for(int k = L[y]; k <= R[y]; ++k) 
			p = dfn[k], s[a[p]][c[p]] = 0; 
	}
	if(son[x]) dfs2(son[x], x); 
	for(int y : G[x]) if(y != fa && y != son[x]) {
		for(int k = L[y]; k <= R[y]; ++k) 
			p = dfn[k], ans += s[a[p]^1][c[p]^c[x]]; 
		for(int k = L[y]; k <= R[y]; ++k) 
			p = dfn[k], s[a[p]][c[p]] ++ ; 
	}
//	for(int y : G[x]) if(y != fa && y != son[x])
	s[a[x]][c[x]]++; 
}

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
//	srand(time(NULL));
//	T=read();
//	while(T--) {
//
//	}
	n=read(); 	
	for(i=1; i<=n; ++i) c[i]=read(); 
	for(i=1; i<n; ++i) {
		u=read(); v=read(); 
		G[u].pb(v); G[v].pb(u); 
	}
	dfs1(1, 0); 
	for(k=0; k<22; ++k) {
		for(i=1; i<=n; ++i) a[i]=(i>>k)&1ll, s[0][c[i]]=s[1][c[i]]=0; 
//		for(i=1; i<=n; ++i) printf("%lld ", a[i]); printf("\n"); 
		ans=0; 
		dfs2(1, 0); 
		sum+=ans*(1ll<<k); 
	}
	
	printf("%lld", sum); 
	return 0;
}