目标和00

news2024/10/6 12:33:03

题目链接

目标和

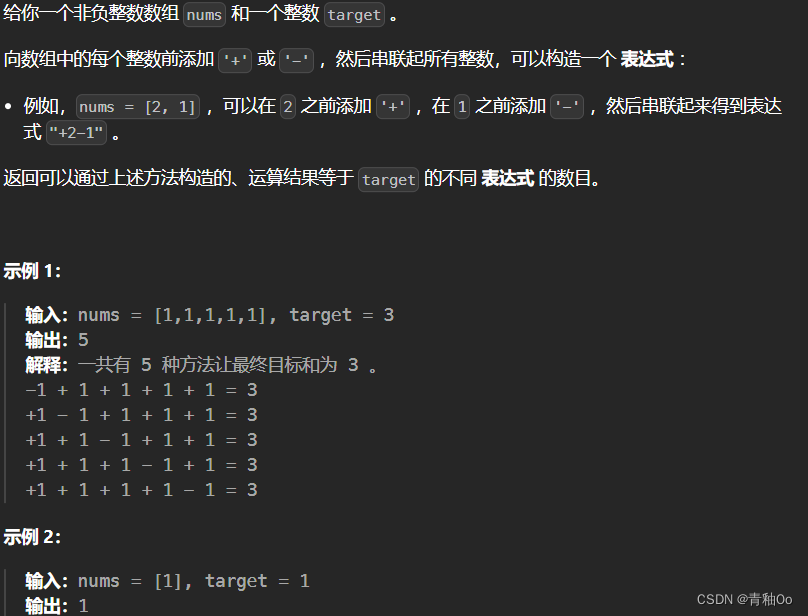
题目描述

注意点

只能向数组中的每个整数前添加 ‘+’ 或 ‘-’
返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
1000 <= target <= 1000

解答思路

第一时间想到的是使用深度优先遍历寻找所有符合题意的组合，但是时间不理想
可将本题看作背包问题，思路为：创建一个行为n + 1列为sum * 2 + 1的dp数组，dp[i][j]表示(0, i)之间能够得到和为(j - 1000)的组合数，列的大小为sum * 2 + 1的原因是数组中所有数字相加相减得到的最大值和最小值分别为sum和-sum，所以需要sum * 2 + 1容量用于存储和为负的情况，在dp中列为sum时视作数组和为0
dp[0][j]表示不选择数组中任何一个数，此时和只有一种情况，就是0，所以dp[0][sum]为1，其余dp[0][j]都为0
可根据dp[i - 1][j]推出dp[i][j - nums[i - 1]]和dp[i][j + nums[i - 1]]，但是要注意边界问题，也就是j - nums[i - 1]为负数和j + nums[i - 1]大于sum * 2时（实际数组中所有数字任意组合也不会超过这个边界）

代码

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int n = nums.length;
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (target - sum > 0 || target + sum < 0) {
            return 0;
        }
        // dp[i][j]表示(0, i)之间能够得到和为(j - 1000)的组合数
        int[][] dp = new int[n + 1][sum * 2 + 1];
        // 不取数字时和为0
        for (int i = 0; i <= n; i++) {
            dp[i][sum] = 1;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < sum * 2 + 1; j++) {
                int comb = 0;
                if (j - nums[i - 1] >= 0) {
                    comb += dp[i - 1][j - nums[i - 1]];
                }
                if (j + nums[i - 1] < sum * 2 + 1) {
                    comb += dp[i - 1][j + nums[i - 1]];
                }
                dp[i][j] = comb;
            }
        }
        return dp[n][target + sum];
    }
}