基于自适应图卷积网络的轨道交通短时客流预测

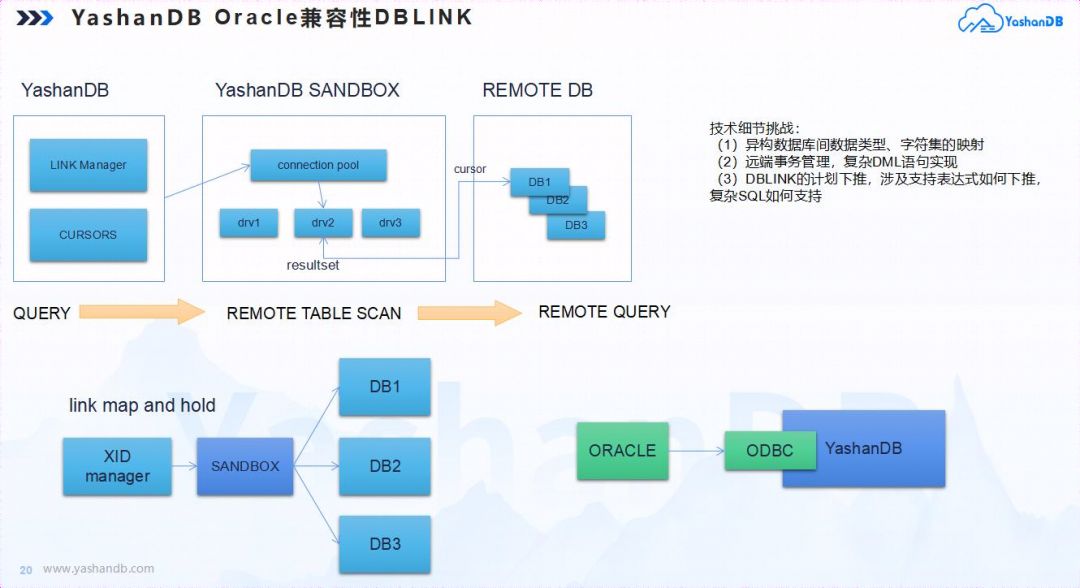
文章信息

论文题目为《Adaptive graph convolutional network-based short-term passenger flow prediction for metro》的一篇2023年5月发表在Journal of Intelligent Transportation Systems的基于自适应图卷积网络的轨道交通短时客流预测文章。

摘要

随着城市化进程的发展和加快，城市轨道交通系统逐渐成长为一个大型网络，站点间的拓扑结构也变得越来越复杂，使得空间依赖性的捕捉变得越来越困难。多条线路的纵横交错使得站点间呈拓扑分布，传统的图卷积网络是基于先验知识生成的邻接矩阵实现的，无法反映站点之间的实际空间依赖性。为了解决这些问题，本文提出了一种自适应图卷积网络模型(Adapt-GCN)，该模型将传统GCN中由先验知识获得的固定邻接矩阵替换为可训练的自适应邻接矩阵。这不仅可以有效地调整相邻站点之间的相关权重，而且可以自适应地捕获非相邻站点之间的空间依赖关系。本文使用上海地铁数据集验证了该模型在提高预测精度和减少训练时间方面的有效性。

介绍

研究意义

随着国内智能交通系统和地铁交通行业的快速发展，智能IC卡开始普及，由此产生了大量的卡数据。在此基础上，可以建立准确有效的客流预测模型，进一步感知客流变化趋势，为城市轨道交通管理者提供有力的决策依据，更好地规划更顺畅的出行路线，为乘客选择更合适的出行时间，从而避免或缓解城市轨道交通拥堵。因此，研究轨道交通客流预测问题具有重要的理论意义和实用价值。

研究综述

关于轨道交通客流预测模型的构建已有大量的研究工作，大致可分为三类。第一类是基于数理统计的模型，如自回归综合移动平均(ARIMA)模型，这类方法只预测了单个站点的客流，这使得唯一可以考虑的因素是时间因素，而不涉及站点之间的空间依赖性。第二类是基于非参数的智能预测模型，如长短期记忆模型（LSTM），这类方法仅对进站或出站的一个方向客流进行预测，并没有实现进站和出站客流的同时预测，这对城市轨道交通的管理部门进行有针对性的安全部署是非常不利的。第三类是基于多特征提取的混合模型，利用卷积神经网络(CNN)从地铁客流图像数据中学习空间特征，并利用双向LSTM从地铁客流时间序列中提取时间特征，最后通过全连接网络融合时空特征，得到客流预测结果，虽然天气、空气条件等多源异构信息的加入可以提高模型的精度，但这些信息的收集和处理难度较大，而且多源数据由于信息冗余和模型结构过于复杂，会导致模型效率低下。

研究贡献

本文主要研究多线路轨道交通网络客流变化的空间特征挖掘，研究思路是基于改进的GCN模型实现对多站进出站客流的同时预测，且要求模型尽可能简单易操作，主要贡献如下：

1、本文研究了地铁客流预测问题，提出了一种新的图卷积模块——自适应图卷积神经网络(Adaptive graph convolution Neural Network, Adapt-GCN)，利用自适应技术捕获相邻和非相邻站点之间的空间相关性。

2、将传统GCN中的固定邻接矩阵替换为可训练的自适应邻接矩阵，通过叠加多个Adaptive-GCN层并加入残差网络实现地铁交通的短时客流预测。

3、我们在真实数据集上进行了大量的实验。实验结果表明，我们的模型始终优于所有基线模型。

问题定义

城市轨道交通客流预测问题是一个典型的时空序列预测问题，利用历史r个时间步的观测结果预测未来时间步的各车站进出站客流。本文定义了一个城市范围的城市轨道交通网络结构图，并利用图卷积神经网络(GCN)学习其空间特征。城市轨道交通网络的常见空间特征包括：由于人口密度和POI分布的影响，使得不同车站客流变化具有较强的相似性；由于受热门路线的影响，不同站点之间的客流方向交互作用明显，例如a站的大部分进站乘客将从b站出站，或者a站的出站乘客将主要来自b站。其中，GCN通常用于提取轨道交通路网的空间特征。

轨道交通网络图

在本研究中，我们将城市轨道交通交通网络定义为一个图。轨道交通网络图由节点、边和边的权重组成，通常用图G=(V; E; A)表示，其中V为所有站点的集合，对应于交通网络中每个地铁站点的观测值，E为边的集合，表示站点间的连通性，A为邻接矩阵，表示站点间的是否相邻。

由上述定义可知，城市轨道交通网络图G属于简单无向图，其中A是一个只有0和1个元素的邻接矩阵，对角元素均为0。对于有n个顶点的简单无向图，拉普拉斯矩阵定义为：L=D-A，其中A为邻接矩阵，D为A的度矩阵，并对拉普拉斯矩阵进行如下的归一化：

客流特征

本文使用客流时间序列数据作为地铁网络中每个站点(节点)的属性特征，表示为，n表示站点个数，r表示属性特征个数，即时间序列的窗口长度，2表示进站和出站客流。如图1所示。图中，Tr表示第r个时间步m个站点的观测客流，Sm表示第m个站点，in_flow和out_flow分别表示进站和出站客流：

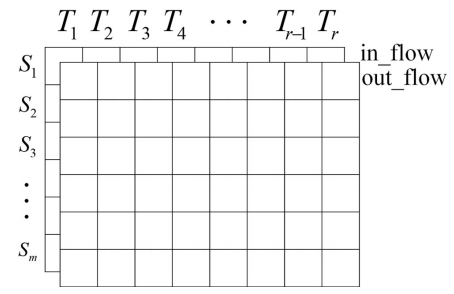
图1 客流特征图

模型算法

图卷积网络（GCN）

在本研究中，作者使用了简化的GCN版本。首先，采用一阶近似设置每个图卷积层来处理相邻一层的邻居特征，然后根据分层传播规则叠加多个图卷积层，达到多层邻居特征传播的效果。其感受野的变化效果图2所示。

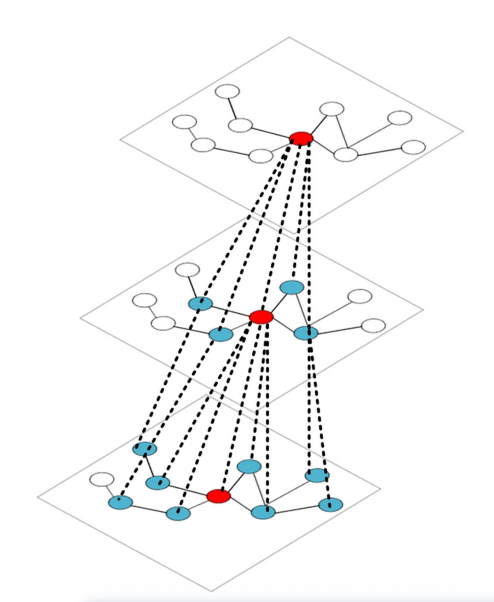
图2 GCN感受野的变化

将原始的图卷积公式经过重新缩放和维数泛化，得到最终的图卷积公式如下：

是一个单位矩阵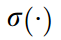，，为激活函数。上式是经过一层GCN的输出，两层堆叠GCN可表示为：

自适应图卷积网络

传统GCN计算公式可以简化为，此处省略了、激活函数和邻接矩阵的归一化。从简化公式来看，传统GCN将卷积过程分为两步，第一步是通过对自身及其相邻节点的特征信息进行聚合，其中可以认为是邻接矩阵，取值范围为0或1。这种聚合仅仅是自身及其邻近节点的特征信息的总和。第二步是W的特征变化，即挖掘节点间的非线性特征，因此W可称为特征变化矩阵。以图2中的简单拓扑网络为例，该图显示了传统GCN公式中的聚合过程，即对自身及其邻居的特征信息进行简单求和。如图3所示，传统GCN的邻接矩阵是固定的，并且在神经网络的整个训练过程中保持不变。

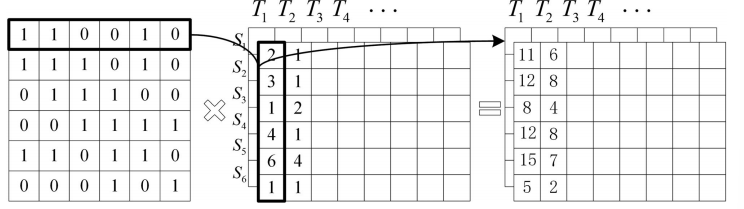
图3 传统GCN

然而，本文认为固定的邻接矩阵使得GCN在聚合节点特征时非常有限，既无法控制自身和相邻节点对结果的影响程度，也无法学习到除自身和相邻节点以外的非相邻节点之间的特征信息。本文设置一个随机初始化的邻接矩阵，通过神经网络的训练进行学习和优化，从而构建一个更适合数据本身的邻接矩阵，该邻接矩阵不需要先验知识，旨在自适应地建模捕获隐藏的空间相关性将这种方法优化后的GCN模型称为自适应图卷积网络(Adaptive graph convolutional network，简称Adapt-GCN)。计算公式如下：

式中，S为Adapt-GCN中随机初始化邻接矩阵，图4为SX在Adapt-GCN中的聚集过程。从图中可以看出，Adapt-GCN中的邻接矩阵S不再是固定的邻接矩阵，而是与邻接矩阵形状相同的随机初始化矩阵。通过对神经网络的训练，不仅可以更自由地学习相邻节点之间的相关性，而且可以通过学习获得非相邻节点之间的相关性。通过将多个Adapt-GCN层叠加并加入残差结构，最后使用融合层，构建本节段地铁交通网络多站进出站客流短时预测模型Adapt-GCN，其结构如图5。

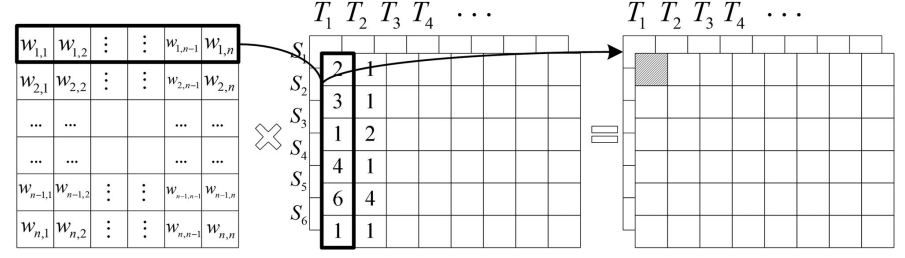
图4 Adapt-GCN

图5 Adapt-GCN模型结构图

实验

数据集

本文客流数据使用上海地铁数据集，该数据集包含288个地铁站点，站点间拓扑分布如下图：

图6 地铁站点分布图

数据范围为2016年7月1日至9月30日，仅对每天5:30-23:45的进出站客流进行预测。对于每个车站，每15分钟统计一次进出站人数，一天共生成73个时间步，92天共生成6716段数据。将所有数据分为训练集、验证集和测试集，大小分别为62天、9天和21天。

评估指标和基准模型

为判断模型的预测效果，采用平均绝对误差(MAE)、均方根误差(RMSE)来量化预测结果的精度，误差计算如下：

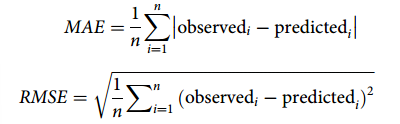
式中，为第i个测试样本的真实流量值，为第i个测试样本的预测流量值，n为测试样本总数。为了验证模型的有效性，选择STGCN、ResNet、ResGCN、JKResGCN四个经典模型与Adapt-GCN进行性能比较。

预测精度分析

在比较模型中，①STGCN采用两个一维时间门控卷积夹在一个图卷积层中间的三明治结构，形成一个时空卷积块，并通过堆叠四个时空卷积块构建深度图卷积网络。虽然该模型可以同时捕获时空特征，但它将CNN1D输出的特征矩阵作为GCN的输入，与直接从原始输入数据中挖掘空间特征相比，导致GCN对空间特征的捕获不足。②ResNet中的CNN结构适用于普通栅格数据，这显然不适用于一般的拓扑地图数据。③在ResNet中叠加多个GCNs的过程中，出现过平滑的现象，过度消除了数据中的变化和细节。④JK-ResGCN在ResGCN的基础上增加了跳跃知识网络，有效解决了过度平滑问题，但跳跃知识网络将每个GCN层的输出以拼接的方式放入最终的融合层，并且随着GCN层的堆叠，融合层的输入通道数量会增加，这使得融合层在特征学习上花费更多的时间。

表1 精度比较

GCN层数量的影响

通过调整GCN的堆叠层数，详细比较了ResGCN、JKResGCN、ResNet和Adapt-GCN四种模型对总客流的预测精度(RMSE)和模型的训练时间。四种模型的对比结果如下图所示。如图所示，无论堆叠GCN层数多少，Adapt-GCN的预测精度都是最优的，尤其是在浅层网络中。这是由于Adaptive-GCN中存在自适应邻接矩阵S，它允许模型捕获浅层网络中较远车站之间的空间相关性。然而，随着数量的增加随着叠加层数的增加，其他三种模型的感受野范围逐渐扩大，Adapt-GCN的精度优势越来越不明显。在训练时间复杂度方面，Adaptive-GCN的训练时间复杂度相对于基于CNN的ResNet要差一些，因为CNN可以更好地进行并行训练。然而，与使用固定邻接矩阵的ResGCN相比，Adapt-GCN特征学习方法变得更加灵活，虽然学习参数的数量增加，但总体训练时间减少。

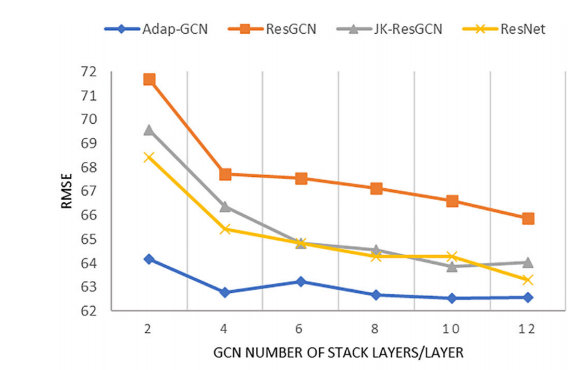
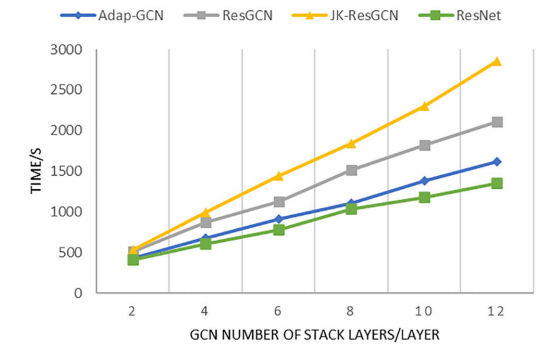
图7 GCN层的影响

消融实验

为了评估模型中组件的有效性，我们设计了消融实验，并在上海地铁数据集上测试了Adapt-GCN的变体。具体来说，Adapt-GCN w/o residual是指Adapt-GCN模型中残差连接块的移除。下表为去除残留连接后的Adapt-GCN预测结果。从表中可以看出，在上海数据集上，Adapt-GCN优于无残差的Adapt-GCN，说明残差连通性对提高预测性能有积极作用。

表2 消融实验

邻接矩阵分析

对于上海地铁数据集，描述车站之间连通性的物理地图（静态邻接矩阵）与单层Adapt-GCN训练获得的自适应邻接矩阵分开可视化。对比结果如下图所示：左图为上海地铁数据集中大小为288×288的物理地图，即固定邻接矩阵A，其中暗区值为1，亮区值为0。不同区域的值分别表示不同站点之间的连通性关系。右图为神经网络训练得到的自适应邻接矩阵S，图中颜色越深表示两站相关性越强，颜色越浅表示相关性越弱。自适应邻接矩阵S和固定邻接矩阵A都有明显的对角线，代表了相邻台站之间的强相关性。此外，自适应邻接矩阵S的取值范围比固定邻接矩阵A的取值范围更广，固定邻接矩阵A只有0和1，这表明自适应邻接矩阵S可以更灵活地学习台站之间的相关性。左图中的浅色区域对应右图中的非零元素，这表明单层的Adapt-GCN也可以捕捉到远距离站之间的空间相关性。

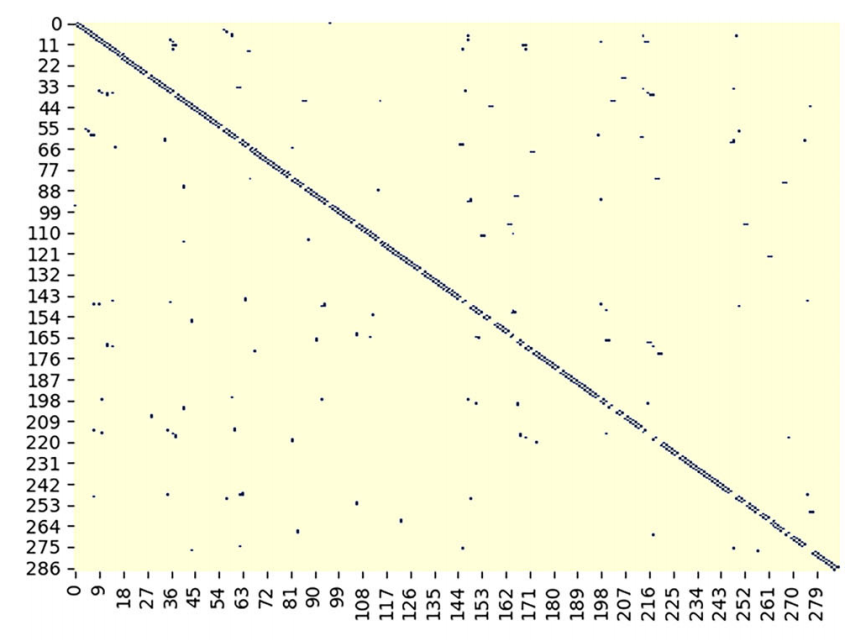
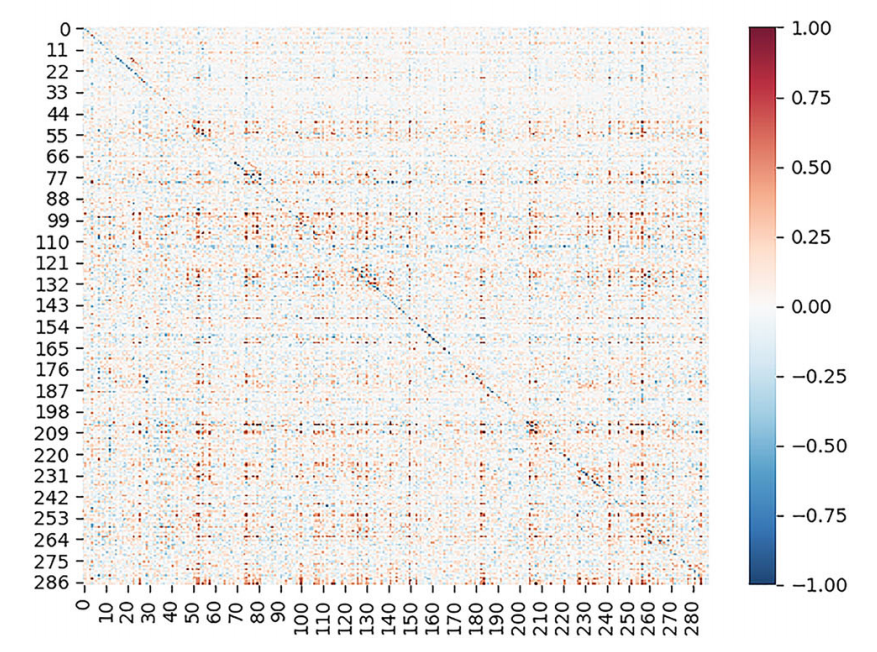
图8 邻接矩阵对比

结论

本文针对于多路线轨道交通网络中的多个站点短时进出站客流预测问题，提出了一种改进的GCN网络。考虑到其站点间在空间分布中的拓扑结构，将传统GCN中的固定邻接矩阵替换为具有相同形状的随机初始化矩阵，并通过神经网络的反向传播过程进行优化。由于该方法不再受固定邻接矩阵的约束，而是允许GCN模型自适应地从数据中学习站之间的拓扑关系，可以充分捕获远距离站之间的空间相关性。实验表明，该模型在实际数据集上的性能优于其他现有方法。另一方面，随机初始化矩阵不再需要真实的站点间拓扑关系，而只需要站点总数，这在很大程度上减轻了邻接矩阵的编制。虽然该模型优于其他方法，但未考虑工作日和周末客流模式差异对客流预测精度的影响。在未来的工作中，我们将更加注重挖掘时间相关性，并考虑时间周期性，例如，每个工作日的早晚高峰通常相似，每个周末的客流模式也相似。我们将考虑时间因素，进一步提高预测精度。