题目
501. 二叉搜索树中的众数
简单
相关标签
树 深度优先搜索 二叉搜索树 二叉树
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
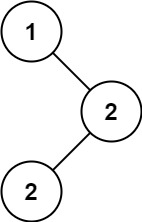
输入:root = [1,null,2,2] 输出:[2]
示例 2:
输入:root = [0] 输出:[0]
提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
思路和解题方法一(暴力)
- 定义一个私有函数
searchBST,用于前序遍历二叉搜索树,并统计每个元素的频率。函数参数包括当前节点指针cur和存储元素频率的unordered_mapmap。- 在
searchBST函数中,如果当前节点为空,则直接返回;否则,对当前节点的值进行统计,将当前节点的值作为map的键,并将对应的值加1,表示该元素出现的频率。- 递归调用
searchBST函数,传入当前节点的左子节点和map,再传入当前节点的右子节点和map,实现前序遍历。- 定义一个静态成员函数
cmp,用于比较两个pair类型的元素,按照频率降序排列。在排序时使用此比较函数。- 在
findMode函数中,首先创建一个空的unordered_map类型的map,用于存储元素及其频率。- 如果输入的根节点为空,直接返回空的结果数组。
- 调用
searchBST函数,传入根节点和map,统计二叉搜索树中每个元素的频率。- 将
map转化为vector类型,并使用sort函数对vector进行排序,排序方式为按照元素的频率降序排列。- 创建一个空的结果数组
result,将排序后的第一个元素的键(也就是出现频率最高的元素)添加到result中。- 遍历排序后的vector,从第二个元素开始,如果其频率和第一个元素的频率相同,则将其键添加到
result中;否则结束遍历。- 返回结果数组
result。
复杂度
时间复杂度:
O(n logn)
时间复杂度:
- 前序遍历二叉树的时间复杂度为 O(n),其中 n 是二叉树的节点数。
- 构建哈希表的过程中,对每个节点进行插入操作的平均时间复杂度为 O(1)。因此构建哈希表的时间复杂度也是 O(n)。
- 对哈希表进行排序的时间复杂度为 O(nlogn)。
- 综上所述,算法的时间复杂度为 O(n) + O(n) + O(nlogn) = O(nlogn)。
空间复杂度
O(n)
空间复杂度:
- 使用了一个哈希表来存储元素及其频率,哈希表的空间复杂度是 O(n)。
- 将哈希表转换成了向量,空间复杂度仍然是 O(n)。
- 保存结果的向量,最多可能存储所有节点的值,因此空间复杂度也是 O(n)。
- 综上所述,算法的空间复杂度为 O(n)。
c++ 代码
class Solution {
private:
// 前序遍历二叉搜索树,统计每个元素的频率
void searchBST(TreeNode* cur, unordered_map<int, int>& map) {
if (cur == NULL) return ;
map[cur->val]++; // 统计元素频率
searchBST(cur->left, map); // 遍历左子树
searchBST(cur->right, map); // 遍历右子树
return ;
}
// 静态成员函数,用于比较两个pair类型元素,按照频率降序排列
static bool cmp(const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
}
public:
vector<int> findMode(TreeNode* root) {
unordered_map<int, int> map; // 存储元素及其频率的map,key为元素,value为频率
vector<int> result; // 结果数组
if (root == NULL) return result; // 根节点为空,直接返回空结果数组
searchBST(root, map); // 统计二叉搜索树中每个元素的频率
vector<pair<int, int>> vec(map.begin(), map.end()); // 将map转换为vector
sort(vec.begin(), vec.end(), cmp); // 按照频率降序排列
result.push_back(vec[0].first); // 将频率最高的元素添加到结果数组中
for (int i = 1; i < vec.size(); i++) {
// 遍历排序后的vector,如果元素频率与第一个元素的频率相同,则添加到结果数组中;否则结束遍历
if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
else break;
}
return result; // 返回结果数组
}
};
思路和解题方法二(双指针 加 时时优化)
- 使用了一个全局变量
maxCount来记录最大频率,使用count来统计当前节点值出现的频率。同时,引入了一个pre变量来记录前一个访问的节点,以便比较当前节点与前一个节点的值是否相同。- 函数
searchBST是进行中序遍历的辅助函数,通过递归遍历左子树、处理当前节点、递归遍历右子树的顺序进行搜索。在处理当前节点时,首先判断当前节点值与前一个节点值是否相同,若相同则将count增加 1,否则将count重置为 1。然后,根据count的大小与maxCount进行比较,并更新maxCount和result。如果count与maxCount相同,说明当前节点值出现的频率与最大频率相同,将其加入result中。如果count大于maxCount,则更新maxCount并清空result,将当前节点值放入result中。- 在
findMode函数中,初始化各个变量,然后调用searchBST开始搜索,并返回结果数组result。
复杂度
时间复杂度:
O(n)
时间复杂度是O(n),其中n是二叉搜索树中的节点数。因为我们需要遍历所有的节点来统计它们的频率。
空间复杂度
O(1)
不利用额外空间
c++ 代码
class Solution {
private:
int maxCount = 0; // 最大频率
int count = 0; // 统计频率
TreeNode* pre = NULL; // 前一个节点
vector<int> result; // 存储结果的向量
// 中序遍历二叉搜索树,搜索出现频率最高的节点值
void searchBST(TreeNode* cur) {
if (cur == NULL) return; // 递归终止条件,当前节点为空
searchBST(cur->left); // 左子树
// 统计频率
if (pre == NULL) { // 第一个节点
count = 1;
} else if (pre->val == cur->val) { // 与前一个节点数值相同
count++;
} else { // 与前一个节点数值不同
count = 1;
}
pre = cur; // 更新上一个节点
if (count == maxCount) { // 如果和最大频率相同,将节点值放进result中
result.push_back(cur->val);
}
if (count > maxCount) { // 如果频率大于最大频率
maxCount = count; // 更新最大频率
result.clear(); // 清空result,之前result中的元素都无效了
result.push_back(cur->val);
}
searchBST(cur->right); // 右子树
return ;
}
public:
vector<int> findMode(TreeNode* root) {
count = 0;
maxCount = 0;
pre = NULL; // 初始化前一个节点为空
result.clear(); // 清空result向量
searchBST(root); // 调用中序遍历函数搜索出现频率最高的节点值
return result; // 返回结果向量
}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。