1. 什么是适配器?
容器适配器是C++标准库中的一种数据结构,它可以将不同类型的容器(如vector、list、deque等)转换为另一种类型的容器。容器适配器提供了一种简单的方式来重新组织和访问数据,同时隐藏了底层容器的实现细节。它们通常用于解决特定的问题或满足特定的需求。
容器适配器有三种常见的类型:栈(stack)、队列(queue)和优先队列
-
栈(stack):栈是一种后进先出(LIFO)的数据结构,类似于现实生活中的一叠盘子。栈容器适配器提供了push、pop、top等操作,可以方便地在栈顶插入和删除元素。
-
队列(queue):队列是一种先进先出(FIFO)的数据结构,类似于现实生活中的排队。队列容器适配器提供了push、pop、front等操作,可以方便地在队列尾部插入元素,在队列头部删除元素。
-
优先队列(priority_queue):优先队列是一种具有优先级的队列,每次取出的元素都是当前队列中优先级最高的元素。优先队列容器适配器提供了push、pop、top等操作,可以方便地插入和删除元素,并且保证每次取出的元素都是最大或最小的。
2. 容器适配器的作用
- 改变容器的接口
- 增加容器的功能
- 限制容器的功能
3. 常见的容器适配
3.1 栈(stack)
3.1.1 概念
栈(stack)是一种常见的容器适配器,它遵循“后进先出”(Last-In-First-Out,LIFO)的原则。栈只允许在末尾进行插入和删除操作,即只能在栈顶进行入栈和出栈操作。

3.1.2 基本操作
| 操作 | 功能 |
|---|---|
| empty | 判空操作 |
| back | 获取尾部元素操作 |
| push_back | 尾部插入元素操作 |
| pop_back | 尾部删除元素操作 |
3.1.3 stack的使用
| 函数说明 | 接口说明 |
|---|---|
| stack() | 构造空的栈 |
| empty() | 检测stack是否为空 |
| size() | 返回stack中元素的个数 |
| top() | 返回栈元素的引用 |
| push() | 将元素val压入stack中 |
| pop() | 将stack中尾部的元素弹出 |
3.1.4 stack的模拟实现
#include<vector>
#include<iostream>
using namespace std;
namespace bite
{
template<class T>
class stack
{
public:
//构造函数
stack()
{}
//入栈
void push(const T& x)
{
_c.push_back(x);
}
//出栈
void pop()
{
_c.pop_back();
}
//返回栈顶元素
T& top()
{
return _c.back();
}
//返回栈顶元素的const版本
const T& top()const
{
return _c.back();
}
//大小
size_t size()const
{
return _c.size();
}
//判断是否为空
bool empty()const
{
return _c.empty();
}
private:
std::vector<T> _c;
};
}
int main()
{
bite::stack<int> mystack;
mystack.push(1);
mystack.push(2);
mystack.push(3);
mystack.push(4);
mystack.push(5);
if (!mystack.empty())
{
cout << "栈大小:" << mystack.size() << endl;
cout << "栈顶元素:" << mystack.top() << endl;
}
mystack.pop();
if (!mystack.empty())
{
cout << "栈大小:" << mystack.size() << endl;
cout << "栈顶元素:" << mystack.top() << endl;
}
}
3.2 队列(queue)
队列是一种常见的容器适配器,它遵循先进先出(FIFO)的原则。在队列中,元素被添加到末尾,被移除时从头部开始。队列适配器提供了一些常用的操作,如入队(enqueue)和出队(dequeue)。
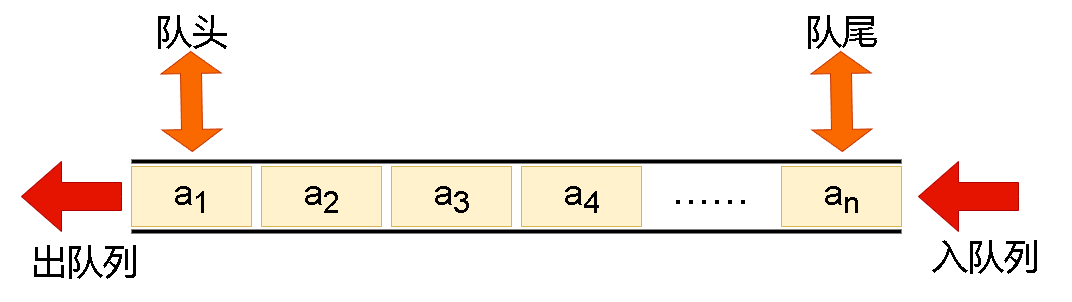
3.2.1 基本操作
| 操作 | 功能 |
|---|---|
| empty | 检队列是否为空 |
| size | 返回队列中有效元素的个数 |
| front | 返回队头元素的引用 |
| back | 返回队尾元素的引用 |
| push_back | 在队列尾部队列 |
| pop_front | 在队列头部出队列 |
3.2.2 queue的使用
| 函数声明 | 接口说明 |
|---|---|
| queue() | 构造空的队列 |
| empty() | 检测队列是否为空,是返回true,否则返回false |
| size() | 返回队列中有效元素的个数 |
| front() | 返回头元素的引用 |
| back() | 返回尾元素的引用 |
| push() | 将队尾元素val入栈 |
| pop() | 将头元素出队列 |
3.2.3 queue的模拟实现
#include<list>
#include<iostream>
using namespace std;
namespace bite
{
template<class T>
class queue
{
public:
//默认构造函数,用于初始化一个新的queue对象
queue()
{}
//入队操作,将元素x添加到队列的末尾
void push(const T& x)
{
_c.push_back(x);
}
//出队操作,移除队列的第一个元素
void pop()
{
_c.pop_front();
}
//返回队列最后一个元素的引用,允许修改
T& back()
{
return _c.back();
}
//返回队列最后一个元素的引用,不允许修改
const T& back() const
{
return _c.back();
}
//返回队列第一个元素的引用,允许修改
T& front()
{
return _c.front();
}
//返回队列第一个元素的引用,不允许修改
const T& front() const
{
return _c.front();
}
//返回队列中元素的个数
size_t size() const
{
return _c.size();
}
//判断队列是否为空
bool empty() const
{
return _c.empty();
}
private:
//用于存储队列中的元素
list<int> _c;
};
}
int main()
{
bite::queue<int> myqueue;
myqueue.push(1);
myqueue.push(2);
myqueue.push(3);
myqueue.push(4);
myqueue.push(5);
if (!myqueue.empty())
{
cout << "队列大小:" << myqueue.size() << endl;
cout << "队列第一个元素:" << myqueue.front() << endl;
cout << "队列最后一个元素:" << myqueue.back() << endl;
}
myqueue.pop();
if (!myqueue.empty())
{
cout << "队列大小:" << myqueue.size() << endl;
cout << "队列第一个元素:" << myqueue.front() << endl;
cout << "队列最后一个元素:" << myqueue.back() << endl;
}
return 0;
}
3.3 优先队列(priority_queue)
3.3.1 概述
优先队列是一种特殊的队列,其中的元素按照一定的优先级进行排序。在优先队列中,每个元素都有一个与之关联的优先级,具有较高优先级的元素会被优先处理。优先队列通常使用堆数据结构来实现,因为堆能够在插入和删除元素时保持元素的有序性。
3.3.2 基本操作
| 操作 | 功能 |
|---|---|
| push | 将一个元素插入到优先级队列中,插入的元素会根据其优先级被放置到合适的位置上 |
| pop | 移除优先队列中具有最高优先级的元素 |
| top | 获取优先队列中具有最高优先级的元素,但不会将其从队列中移除 |
| empty | 检查优先队列是否为空 |
3.3.3 priority_queue的使用
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:默认情况下priority_queue是大堆。
| 函数声明 | 接口说明 |
|---|---|
| priority_queue()/priority_queue(first, last) | 构造一个空的优先级队列 |
| empty() | 检测优先级队列是否为空,是返回true,否则返回false |
| top() | 返回优先级队列中最大(最小元素),即堆顶元素 |
| push(x) | 在优先级队列插入元素x |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
3.3.4 实现方式
优先队列可以通过堆来实现,常见的堆有大堆和小堆。大堆中,根节点的值最大,每个节点的值都大于或等于其子节点的值;小堆中,根节点的值最小,每个节点的值都小于或等于其子节点的值。优先队列可以根据元素的优先级来构建最大堆或最小堆
3.3.5 基本操作和时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| 插入元素 | O(long n) |
| 删除元素 | O(long n) |
| 获取元素首元素 | O(1) |
| 判断队列是否为空 | O(1) |
3.3.6 priority_queue的模拟实现
#pragma once
#include <iostream>
using namespace std;
#include <vector>
// priority_queue--->堆
namespace bite
{
template<class T>
struct less
{
bool operator()(const T& left, const T& right)
{
return left < right;
}
};
template<class T>
struct greater
{
bool operator()(const T& left, const T& right)
{
return left > right;
}
};
template<class T, class Container = std::vector<T>, class Compare = less<T>>
class priority_queue
{
public:
// 创造空的优先级队列
priority_queue() : c() {}
template<class Iterator>
priority_queue(Iterator first, Iterator last)
: c(first, last)
{
// 将c中的元素调整成堆的结构
int count = c.size();
int root = ((count - 2) >> 1);
for (; root >= 0; root--)
AdjustDown(root);
}
void push(const T& data)
{
c.push_back(data);
AdjustUP(c.size() - 1);
}
void pop()
{
if (empty())
return;
swap(c.front(), c.back());
c.pop_back();
AdjustDown(0);
}
size_t size()const
{
return c.size();
}
bool empty()const
{
return c.empty();
}
// 堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性
const T& top()const
{
return c.front();
}
private:
// 向上调整
void AdjustUP(int child)
{
int parent = ((child - 1) >> 1);
while (child)
{
if (Compare()(c[parent], c[child]))
{
swap(c[child], c[parent]);
child = parent;
parent = ((child - 1) >> 1);
}
else
{
return;
}
}
}
// 向下调整
void AdjustDown(int parent)
{
size_t child = parent * 2 + 1;
while (child < c.size())
{
// 找以parent为根的较大的孩子
if (child + 1 < c.size() && Compare()(c[child], c[child + 1]))
child += 1;
// 检测双亲是否满足情况
if (Compare()(c[parent], c[child]))
{
swap(c[child], c[parent]);
parent = child;
child = parent * 2 + 1;
}
else
return;
}
}
private:
Container c;
};
}
void TestQueuePriority()
{
bite::priority_queue<int> q1;
q1.push(5);
q1.push(1);
q1.push(4);
q1.push(2);
q1.push(3);
q1.push(6);
cout << q1.top() << endl;
q1.pop();
q1.pop();
cout << q1.top() << endl;
vector<int> v{ 5,1,4,2,3,6 };
bite::priority_queue<int, vector<int>, bite::greater<int>> q2(v.begin(), v.end());
cout << q2.top() << endl;
q2.pop();
q2.pop();
cout << q2.top() << endl;
}
4. 容器适配器的优点
4.1 封装性
容器适配器隐藏了底层容器的实现细节,只暴露出特定的接口,使得使用者可以方便地操作容器适配器,而不需要了解底层容器的具体实现。
4.2 灵活性
容器适配器可以根据不同的需求选择不同的底层容器来实现功能。例如,可以使用栈来实现适配器,也可以使用队列来实现适配器,这取决于具体的使用场景和要求。
4.3 功能拓展
容器适配器可以根据需要进行扩展,添加新的功能或修改现有功能。由于适配器与底层容器解耦,因此可以独立地对适配器进行修改,而不会影响到其他部分的代码。
4.4 与标准库兼容
容器适配器通常与标准库的容器接口兼容,这意味着可以通过容器适配器来替换标准容器的使用,而不需要修改其他代码。