哈夫曼树及哈夫曼编码详解及代码实现[C/C++]

文章目录

哈夫曼树及哈夫曼编码
- 哈夫曼树的定义与原理
- - 引例
  - 路径长度
  - - 定义
  - 带权路径长度
  - 哈夫曼树
  - 哈夫曼树的构造方法
  - - 构造方法示例
- 哈夫曼树的代码实现
- - 哈夫曼树的结点定义
  - 哈夫曼树的构造
- 哈夫曼编码
- - 哈夫曼编码方式
  - 哈夫曼编码解码的准确性
- 哈夫曼编码的代码实现
- - 运行示例

哈夫曼树及哈夫曼编码

在日常的网络办公中，文件压缩是一种常见的节省空间提高效率的操作，那么这种压缩技术是如何实现的呢？其实就是对我们要传输的文本进行重新编码，以减少不必要的空间。。尽管现在最新技术在编码上已经很好很强大，但这一切都来自于曾经的技术积累，我们今天就来介绍-一下最基本的压缩编码方法——哈夫曼编码。

哈夫曼树的定义与原理

1951年，哈夫曼在MIT信息论课程的导师Robert M. Fano给他们两个选择，一是完成学期报告的题目：寻找最有效的二进制编码，二是完成期末考试。只能说大佬不愧是大佬，毅然决然选择了第一种方式，弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法并很快证明了这个方法是最有效的。由于这个算法，学生终于青出于蓝，超过了他那曾经和信息论创立者香农共同研究过类似编码的导师。

为了更好地接受哈夫曼树的概念，我们来看下面这个引例。

引例

过去我们小学、中学一般考试都是用百分制来表示学科成绩的。但为了避免以分取人的现象，如今很多学科特别是小学学科学科成绩都改作了优秀、良好、中等、及格和不及格这样模糊的词语。

不过对于老师来讲，他在对试卷评分的时候，显然不能凭感觉给优良或及格不及格等成绩，因此一般都还是按照百分制算出每个学生的成绩后，再根据统一的标准换算得出五级分制的成绩。比如下面的代码就实现了这样的转换。

if (a < 60)
b="不及格”;
else if (a < 70)
b="及格“;
else if (a < 80)
b="中等" ;
else if (a < 90)
b="良好“;
else
b="优秀" ;

下图粗略看没什么问题，可是通常都认为，一张好的考卷应该是让学生成绩大部分处于中等或良好的范围，优秀和不及格都应该较少才对。而上面这样的程序，就使得所有的成绩都需要先判断是否及格，再逐级而上得到结果。输入量很大的时候，其实算法是有效率问题的。

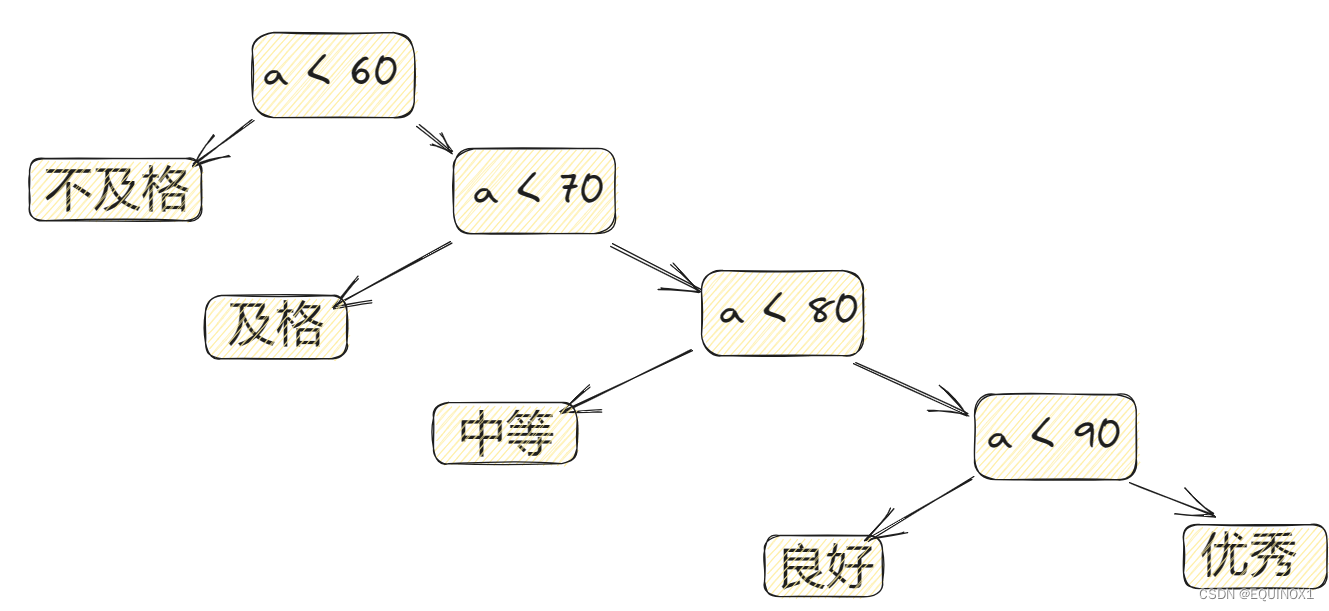
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

如果在实际的学习生活中，学生的成绩在5个等级上的分布规律如下表所示。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

对于大于70分共80%的成绩都要经过至少三次判断才可以得到结果，这显然不合理，那么有没有好一些的办法呢？

我们有一个思想叫做加速大概率时间(make the common fast)，我们发现中等成绩(70_{79)的比例最高，其次是良好(80}89)，那么我们基于加速大概率事件的思想，把上图二叉树重新分配，变成如下图的样子。

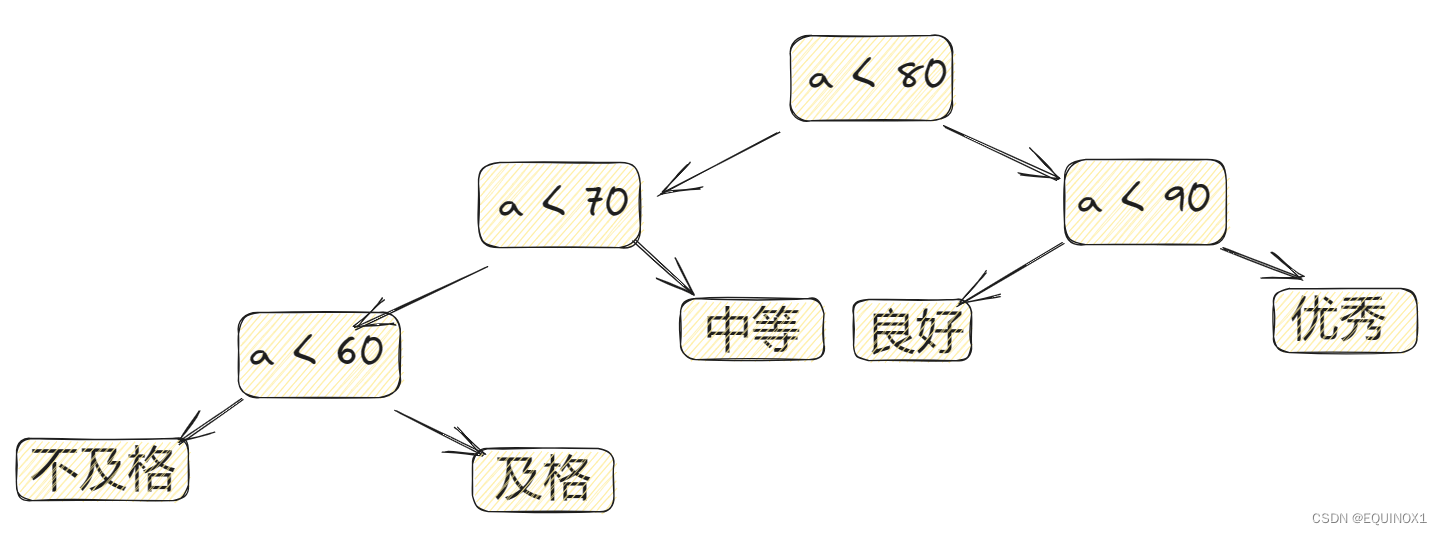
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

如此一来，我们的效率应该要高一些了，但是这种二叉树是如何构造出来的呢？

路径长度

定义

从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。树的路径长度即树根到每一结点的路径长度之和。

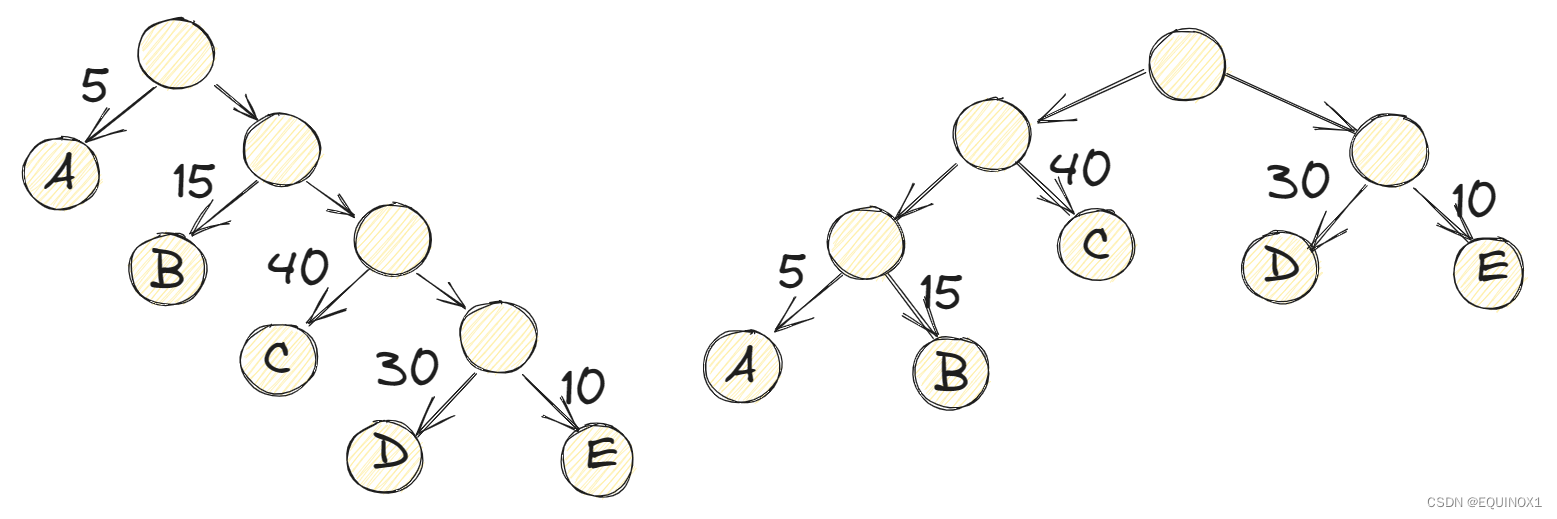
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

如上图左边二叉树根到D的路径长度就是4，右边二叉树根到D路径长度为2.

左树的路径长度为1+1+2+2+3+3+4+4=20，右树的路径长度为1+2+3+3+2+1+2+2=16。

带权路径长度

**结点的带权路径长度(WPL)**为从该节点到树根之间的路径长度与结点上权的乘积。

哈夫曼树

带权路径长度(WPL)最小的二叉树称做哈夫曼树(Huffman Tree)，不少书中也称为最优二叉树。

现在有了带权路径长度(WPL)的定义，我们计算下上图两颗二叉树的WPL值。

左树WPL：5*1 + 15*2 + 40*3 + 30*4 +10*4 = 315
右树WPL：5*3 + 15*2 + 40*2 + 30*2 +10*2 = 220

这意味着什么？
我们如果有10000个学生的百分制成绩需要转化为五级分制成绩的话，用左树的方法要做315 * 10000 * 0.01 = 31500次，对于右树只需要22000次！性能大大提升

哈夫曼树的构造方法

对于哈夫曼树构造方法的正确性很多教材书上都有，有兴趣的自行查阅，这里仅给出构造方法。

(1)根据给定的n个权值{ w1，w2，……wn }构成n棵二叉树的集合F=(T1、T2……Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点，其左右子树均为空。
(2)在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
(3)在F中删除这两棵树，同时将新得到的二叉树加入F中。
(4)重复步骤(2)和(3)，直到F只含一棵树为止。这棵树便是哈夫曼树。

构造方法示例

先以上图左树给出示例
(1)先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列，即A5，E10，B15，D30，C40。
(2)取头两个最小权值的结点作为一个新结点N1的两个子结点，注意相对较小的是左孩子，这里就是A为N1的左孩子，E为N1的右孩子，如下图所示。新结点的权值为两个叶子权值的和5+10=15。
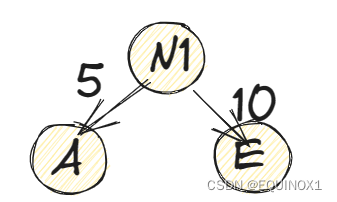
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

(3)将N1替换A与E，插入有序序列中，保持从小到大排列。即N1，15。 B1S，D30，C40。
(4)重复步骤(2)。将N1与B作为一个新结点N2的两个子结点。如下图所示。N2的权值=15+15=30.
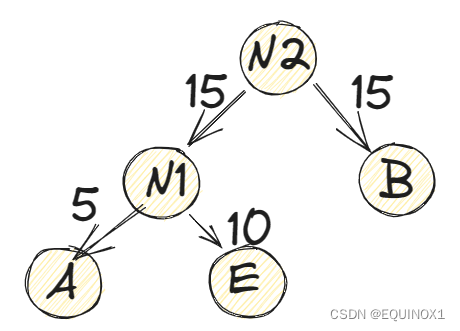
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

(5)将N2替换N1与B，插入有序序列中，保持从小到大排列。即N2，30， D30， C40。
(6)重复步骤(2)。将N2与D作为一个新结点N3的两个子结点。如下图所示。N3的权值=30+30=60. .

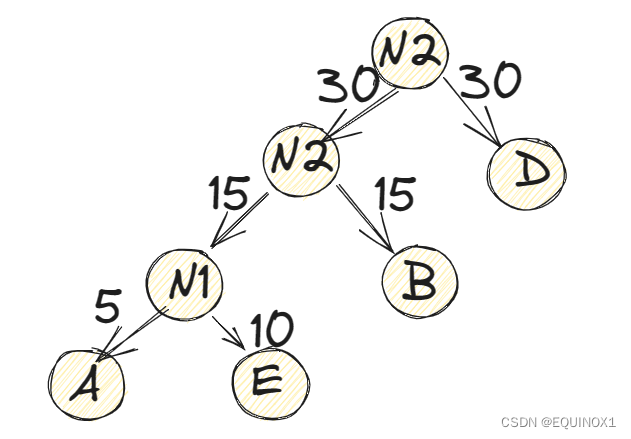
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

(7)将N3替换N2与D，插入有序序列中，保持从小到大排列。即C40,，N3，60。
(8)重复步骤(2)。将C与N3作为一个新结点T的两个子结点，如左下图所示。由于T即是根结点，完成哈夫曼树的构造。
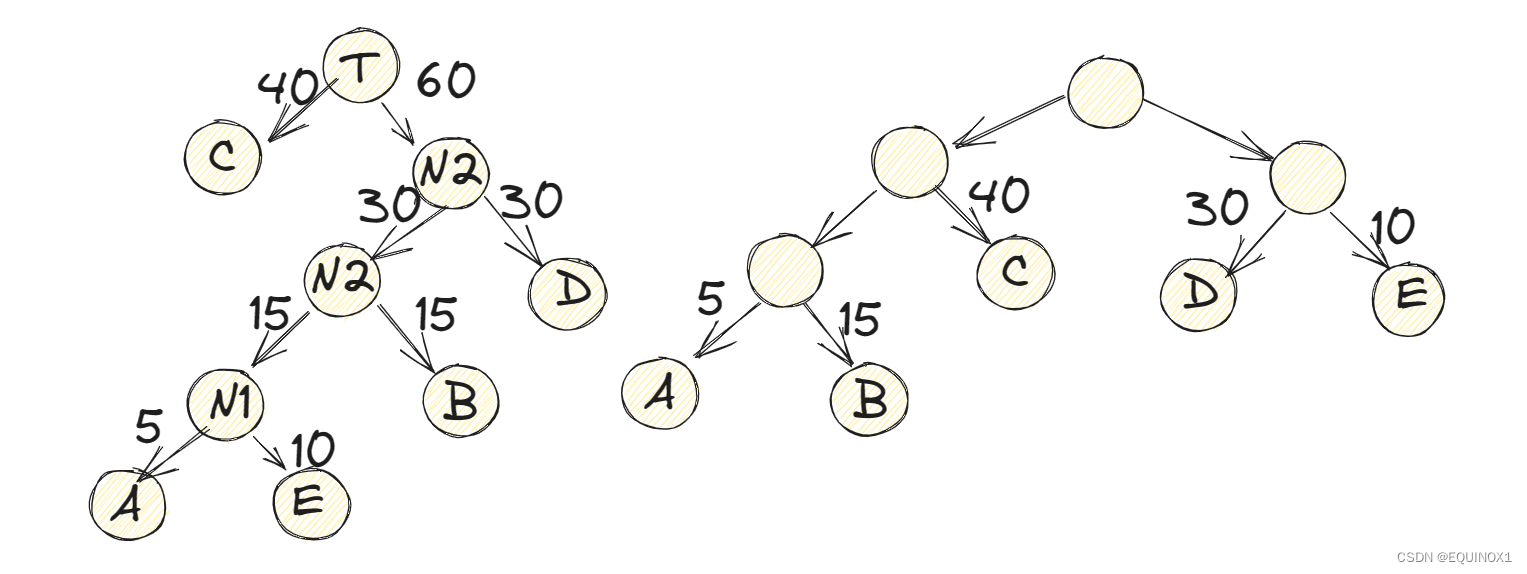
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

此时的左上图二叉树的带权路径长度WPL=40x1+30x2+15x3+10x4+5x4=205.与右上图二叉树的WPL=5x3+15x3+40x2+30x2+10x2= =220相比，还少了15。显然此时构造出来的二叉树才是最优的哈夫曼树。

哈夫曼树的代码实现

哈夫曼树的结点定义

template <class T = double>
struct HuffmanTreeNode
{
    HuffmanTreeNode(const T &w = T(), int l = 0, int r = 0, int p = 0) : _weight(w), _left(l), _right(r), _parent(p)
    {
    }
    T _weight;//权值
    int _left;//左孩子
    int _right;//右孩子
    int _parent;//父节点
};

哈夫曼树的构造

我们初始有n个叶子结点，构建过程中每次减少一个结点，最后只剩一个结点，也就是说我们增加了n - 1个扩展结点，最后一共有2 * n - 1个结点。

我们选择用数组来实现这一树形结构，由于有2 * n - 1个结点，我们开2 * n空间的数组，多出来的一个位置作为叶子节点的空指针域

对于每次取两个最小权值叶子结点的操作，我们可以把所有叶子结点放入小根堆(用C++的priority_queue)内，每次弹出两个结点，再将新结点压入，这样即保证了每次取出两个最小权值的结点，又保证了不会取到扩展结点的叶子结点

哈夫曼树构造函数代码如下：

    HuffmanTree(int n, const vector<T> &weights)
    {
        _HT.resize(2 * n); // 开辟2 * n的空间
        int i = 0, newweight = 0, l = 0, r = 0;

        function<bool(const pair<T, int> &, const pair<T, int> &)> cmp = [&n](const pair<T, int> &p1, const pair<T, int> &p2) -> bool
        {
            return p1.first > p2.first || ((p1.first == p2.first) && ((p1.second > n || p2.second > n) && p1.second < p2.second)) || ((p1.first == p2.first) && ((p1.second <= n && p2.second <= n) && p1.second > p2.second));
        };//这里比较条件保证小根堆，如果权值相同，如果是扩展结点那么扩展结点优先下标大的在前，两个不含扩展结点，那么下标小的优先在前
        //由于哈夫曼树不是唯一的，所以这里的判断条件也不是唯一的，只是我们和我们的示例吻合

        priority_queue<pair<T, int>, vector<pair<T, int>>, function<bool(const pair<T, int> &, const pair<T, int> &)>> pq(cmp);
        for (i = 0; i < n; i++)
        {
            _HT[i + 1] = Node(weights[i]);
            pq.emplace(make_pair(weights[i], i + 1));
        } // 先把给定的叶子节点都放入小根堆内
        for (i = 1; i < n; i++)
        {
            newweight = 0;
            l = pq.top().second;
            newweight += pq.top().first;
            pq.pop();
            r = pq.top().second;
            newweight += pq.top().first;
            pq.pop();
            _HT[n + i] = Node(newweight, l, r); // newweight即为扩展结点的权值，孩子分别为l和r

            _HT[l]._parent = _HT[r]._parent = n + i; // 把孩子结点的_parent置位n + i
            pq.emplace(make_pair(newweight, n + i)); // 把新结点放入小根堆内
        }
        // 打印我们哈夫曼树的信息，验证我们哈夫曼树是否正确
        printf("HuffmanTree各结点信息:\n");
        printf("%-6s%-8s%-8s%-8s%-9s\n", "下标", "权值", "左孩子", "右孩子", "父亲");

        for (int i = 1; i < n * 2; i++)
        {
            printf("%-6d%-8.2lf%-8d%-8d%-8d\n", i, _HT[i]._weight, _HT[i]._left, _HT[i]._right, _HT[i]._parent);
        }
    }

哈夫曼编码

当然，哈夫曼研究这种最优树的目的不是为了我们可以转化一下成绩。他的更大目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题。

比如我们有一段文字内容“BADCADFEED”要通过网络传输给别人，显然用二进制的数字(0和1)来表示是很自然的想法。现在这段文字只有六个字母A、B、C、D、E、F，那么我们可以用相应的二进制字符表示，如下表所示。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

这样真正传输的数据就是编码后的“001000011010000011101100100011”，对方接收时可以按照三位一分来译码。如果一篇文章很长，这样的二进制串也将非常的可怕。但任何语言文本中，不同字符的出现频率显然不同。

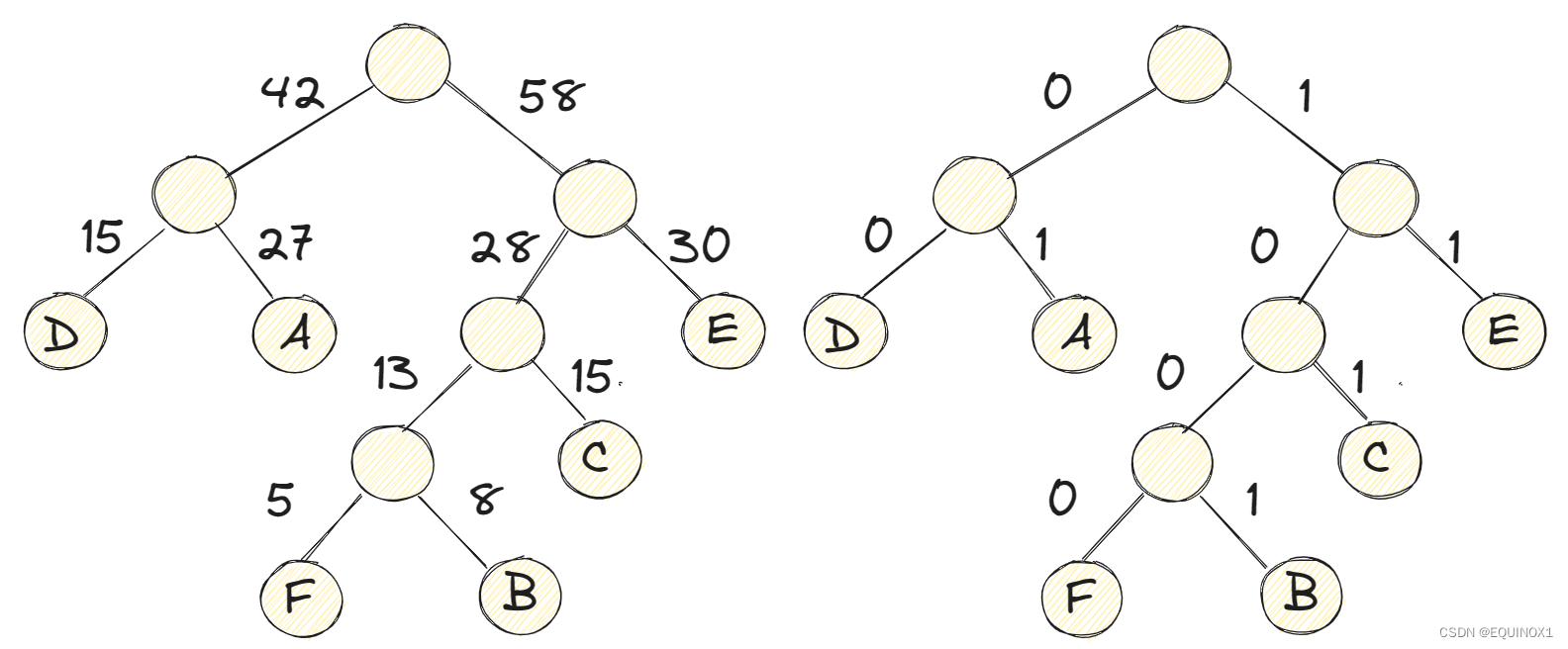
仍然是基于加速大概率事件的思想，我们假设六个字母频率为A27，B8，C15，D 15， E30，F5，合起来刚好100%。那就意味着，我们完全可以重新按照哈夫曼树来规划它们。

哈夫曼编码方式

我们先以频率为权值建立哈夫曼树，然后将每个结点的左分支权值设置为0，右分支设置为1，就得到了如下哈夫曼树

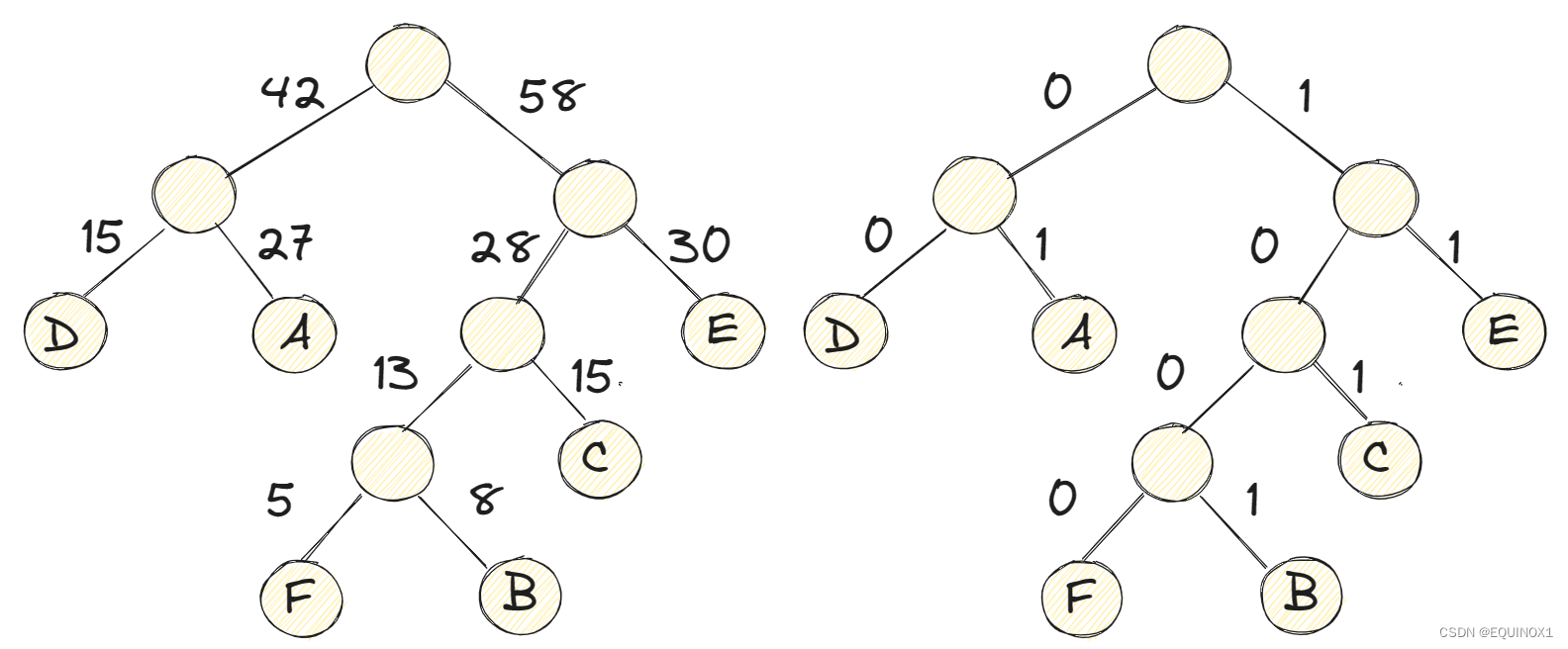
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

此时，我们对这六个字母用其从树根到叶子所经过路径的0或1来编码，可以得到如下表所示这样的定义。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

我们将文字内容“BADCADFEED”再次编码，对比可以看到结果串变小了。

原编码二进制串: 001000011010000011101100100011 (共30个字符)
新编码二进制串: 1001010010101001000111100 (共25个字符)

也就是说，我们的数据被压缩了，节约了大约17%的存储或传输成本。随着字符的增加和多字符权重的不同，这种压缩会更加显出其优势。

哈夫曼编码解码的准确性

当我们接收到10010100101010001011100这样压缩过的新编码时，我们应该如何把它解码出来呢?
编码中非0即1，长短不等的话其实是很容易混淆的，所以若要设计长短不等的编码，则必须是任一字符的编码都不是另一个字符的编码的前缀，这种编码称做前缀编码。

你仔细观察就会发现，上表中的编码就不存在容易与1001、1000混淆的“10” 和“100”编码。我们哈夫曼编码的解码具有优越的准确性。
可仅仅是这样是不足以让我们去方便地解码的，因此在解码时，还是要用到哈夫曼树，即发送方和接收方必须要约定好同样的哈夫曼编码规则。
当我们接收到10010100101010000111100时，由约定好的哈夫曼树可知，1001得到第一个字母是B，接下来01意味着第二个字符是A，如下图所示，其余的也相应的可以得到，从而成功解码。

一般地，设需要编码的字符集为{ d1，d2，……，dn },各个字符在电文中出现的次数或频率集合为{ W1，W2……，Wn }，以d1，d2……dn作为叶子结点，以w1，w2……wn作为相应叶子结点的权值来构造一棵哈夫曼树。规定哈夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码，这就是哈夫曼编码。

哈夫曼编码的代码实现

对于我们的编码长度一定不大于我们叶子节点的个数，也就是说我们开一个长度为n的字符串来存储我们的Huffman编码即可

我们知道叶子节点的下标，从叶子结点往上找parent得到的编码是逆序的，所以我们用一个指针start从后往前存放编码

最终的编码就是code.substr(start + 1 , len)（由于从start + 1到末尾都是编码所以len可以省略）

代码如下：

    void HuffmanCode()
    {
        int n = _HT.size() / 2; //_HF开了2 * n个空间
        vector<string> codes;
        string code(n, '\0');
        int i = 1, start = n - 1, parent = 0, child = 0;

        for (i = 1; i <= n; i++)
        {
            start = n - 1;
            child = i;
            parent = _HT[child]._parent;
            while (parent)
            {
                if (_HT[parent]._left == child)
                    code[start--] = '0';
                else
                    code[start--] = '1';
                child = parent;
                parent = _HT[parent]._parent;
            }
            codes.emplace_back(code.substr(start + 1));
        }

        printf("各数据的Huffman编码为:\n");
        for (i = 0; i < n; i++)
        {
            cout << "数据" << i + 1 << ":" << codes[i] << endl;
        }
    }

运行示例

我们以下图为例，展示代码运行结果

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

示例代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
#include <queue>
using namespace std;
template <class T = double>
struct HuffmanTreeNode
{
    HuffmanTreeNode(const T &w = T(), int l = 0, int r = 0, int p = 0) : _weight(w), _left(l), _right(r), _parent(p)
    {
    }
    T _weight;   // 权值
    int _left;   // 左孩子
    int _right;  // 右孩子
    int _parent; // 父节点
};
template <class T = double>
class HuffmanTree
{
private:
    typedef HuffmanTreeNode<T> Node;

public:
    HuffmanTree(int n, const vector<T> &weights)
    {
        _HT.resize(2 * n); // 开辟2 * n的空间
        int i = 0, newweight = 0, l = 0, r = 0;

        function<bool(const pair<T, int> &, const pair<T, int> &)> cmp = [&n](const pair<T, int> &p1, const pair<T, int> &p2) -> bool
        {
            return p1.first > p2.first || ((p1.first == p2.first) && ((p1.second > n || p2.second > n) && p1.second < p2.second)) || ((p1.first == p2.first) && ((p1.second <= n && p2.second <= n) && p1.second > p2.second));
        }; // 这里比较条件保证小根堆，如果权值相同，如果是扩展结点那么扩展结点优先下标大的在前，两个不含扩展结点，那么下标小的优先在前

        priority_queue<pair<T, int>, vector<pair<T, int>>, function<bool(const pair<T, int> &, const pair<T, int> &)>> pq(cmp);
        for (i = 0; i < n; i++)
        {
            _HT[i + 1] = Node(weights[i]);
            pq.emplace(make_pair(weights[i], i + 1));
        } // 先把给定的叶子节点都放入小根堆内
        for (i = 1; i < n; i++)
        {
            newweight = 0;
            l = pq.top().second;
            newweight += pq.top().first;
            pq.pop();
            r = pq.top().second;
            newweight += pq.top().first;
            pq.pop();
            _HT[n + i] = Node(newweight, l, r); // newweight即为扩展结点的权值，孩子分别为l和r

            _HT[l]._parent = _HT[r]._parent = n + i; // 把孩子结点的_parent置位n + i
            pq.emplace(make_pair(newweight, n + i)); // 把新结点放入小根堆内
        }
        // 打印我们哈夫曼树的信息，验证我们哈夫曼树是否正确
        printf("HuffmanTree各结点信息:\n");
        printf("%-6s%-8s%-8s%-8s%-9s\n", "下标", "权值", "左孩子", "右孩子", "父亲");

        for (int i = 1; i < n * 2; i++)
        {
            printf("%-6d%-8.2lf%-8d%-8d%-8d\n", i, _HT[i]._weight, _HT[i]._left, _HT[i]._right, _HT[i]._parent);
        }
    }

    void HuffmanCode()
    {
        int n = _HT.size() / 2; //_HF开了2 * n个空间
        vector<string> codes;
        string code(n, '\0');
        int i = 1, start = n - 1, parent = 0, child = 0;

        for (i = 1; i <= n; i++)
        {
            start = n - 1;
            child = i;
            parent = _HT[child]._parent;
            while (parent)
            {
                if (_HT[parent]._left == child)
                    code[start--] = '0';
                else
                    code[start--] = '1';
                child = parent;
                parent = _HT[parent]._parent;
            }
            codes.emplace_back(code.substr(start + 1));
        }

        printf("各数据的Huffman编码为:\n");
        for (i = 0; i < n; i++)
        {
            cout << "数据" << i + 1 << ":" << codes[i] << endl;
        }
    }

private:
    vector<Node> _HT;
};
int main()
{
    vector<double> weights{27, 8, 15, 15, 30, 5};
    HuffmanTree<double> ht(6, weights);
    ht.HuffmanCode();
    return 0;
}

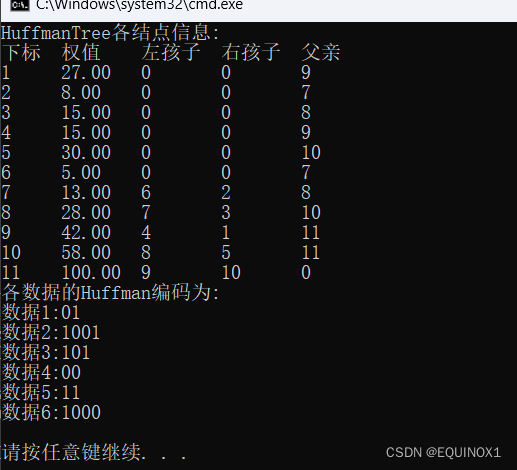
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传