引言

上一节介绍了$\text{RMSProp}$算法，本节在其基础上进行延伸，介绍基于$\text{Nesterov}$动量的$\text{RMSProp}$算法。

回顾：优化方式区别

在前面介绍的多种算法：动量法、$\text{Nesterov}$动量法、$\text{AdaGrad}$算法、$\text{RMSProp}$算法，其本质上均是针对梯度下降法的优化方法。从优化方式的角度划分，可以将上述方法分为两类：

• 对梯度方向进行优化。对应算法：动量法、$\text{Nesterov}$动量法。它们的共同点是均利用了历史累积梯度对当前梯度进行优化。两者的不同点在于：

  • 动量法是通过当前迭代步骤梯度${\nabla }_{\theta ;t-1}\mathcal{J}({\theta }_{t-1})$与历史累积梯度$m_{t-1}$进行加权运算(向量加法)，从而得到当前迭代步骤更新梯度$m_t$：
    $$\{\begin{array}{l}{m}_t=\beta \cdot m_{t-1}+(1-\beta )\cdot {\nabla }_{\theta ;t-1}\mathcal{J}({\theta }_{t-1})\\ {\theta }_t={\theta }_{t-1}-\eta \cdot m_t\end{array}$$
  • 而$\text{Nesterov}$动量法则是通过历史累积梯度$m_{t-1}$与超前梯度信息${\nabla }_{\theta ;t-1}\mathcal{J}({\theta }_{t-1}+\gamma \cdot m_{t-1})$进行加法运算的方式得到$m_t$：
    $$\{\begin{array}{l}{m}_t=\beta \cdot m_{t-1}+(1-\beta )\cdot {\nabla }_{\theta ;t-1}({\theta }_{t-1}+\gamma \cdot m_{t-1})\\ {\theta }_t={\theta }_{t-1}-\eta \cdot m_t\end{array}$$

• 对梯度大小(学习率)进行优化。对应算法：$\text{AdaGrad}$算法、$\text{RMSProp}$算法。它们的不同点仅在：$\text{RMSProp}$算法在$\text{AdaGrad}$算法基础上利用指数加权移动平均法来弱化初始迭代步骤的累积平方梯度对当前迭代步骤的影响，从而大幅增加收敛速度：
  $$\begin{array}{rl}\text{AdaGrad : }& \{\begin{array}{l}{\mathcal{G}}_t={\nabla }_{\theta ;t-1}\mathcal{J}({\theta }_{t-1})\\ {\mathcal{R}}_t={\mathcal{R}}_{t-1}+{\mathcal{G}}_t\odot {\mathcal{G}}_t\\ \begin{array}{r}{\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{{\mathcal{R}}_t}+ϵ}\odot {\mathcal{G}}_t\end{array}\end{array}\\ \text{RMProp : }& \{\begin{array}{l}{\mathcal{G}}_t={\nabla }_{\theta ;t-1}\mathcal{J}({\theta }_{t-1})\\ {\mathcal{R}}_t=\beta \cdot {\mathcal{R}}_{t-1}+(1-\beta )\cdot {\mathcal{G}}_t\odot {\mathcal{G}}_t\\ \begin{array}{r}{\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{{\mathcal{R}}_t}+ϵ}\odot {\mathcal{G}}_t\end{array}\end{array}\end{array}$$

但上述两类优化方法由于针对梯度的不同角度(梯度方向、梯度大小)，因而两者之间互不影响。本节将两种优化思想共同作用在一个算法中，即：基于$\text{Nesterov}$动量的$\text{RMSProp}$算法。

(2023/10/11) 关于指数加权移动平均法的补充

在之前深度学习优化算法中，关于指数加权移动平均法，我们有意的避开一些点。但在基于$\text{Nesterov}$动量的$\text{RMSProp}$算法中，由于梯度方向、梯度大小(学习率) 均使用了指数加权移动平均法，关于《深度学习(花书)》中的算法描述，这里简单描述两类加权方法之间的区别。

• 在《深度学习(花书)》中，关于动量的加权平均方法表示如下：
  详见《深度学习(花书)》P182 8.3.2动量 算法8.2
  $$\{\begin{array}{l}{m}_t=\gamma \cdot m_{t-1}-\eta \cdot \mathcal{G}\\ {\theta }_t={\theta }_{t-1}+m_t\end{array}$$
• 它与我们在$\text{Nesterov}$动量法的简单认识中介绍动量法中的加权平均方法存在一些区别：
  $$\{\begin{array}{l}{m}_t=\beta \cdot m_{t-1}+(1-\beta )\cdot \mathcal{G}\\ {\theta }_t={\theta }_{t-1}+\eta \cdot m_t\end{array}$$

第二种描述明显是：将历史梯度信息$m_{t-1}$与当前迭代步骤梯度信息$\mathcal{G}$按比例分配；而书中的描述仅将历史梯度信息$m_{t-1}$固定削减一个比例，而对当前迭代步骤梯度$\mathcal{G}$不进行理会。但我们不否认的是：虽然后者更加简便，但依然能够达到适当地丢弃遥远过去的历史梯度信息。

在书中基于$\text{Nesterov}$动量的$\text{RMSProp}$算法中，关于上述两种加权平均方法：
如果有机会，也可以将其均改成第一种或者第二种加权平均方法，观察它们之间的关系(挖个坑)~

• 对于梯度方向(动量) 的加权平均，它使用的是第一种方式；
• 对于梯度大小(学习率) 的加权平均，它使用的是第二种方式；

算法过程描述

算法步骤表示如下：
初始化操作：

• 学习率$\eta$；衰减因子$\beta$；动量因子$\gamma$；
• 初始化参数$\theta$；初始动量$m$；梯度累积信息$\mathcal{R}=0$

算法过程：

• $\text{While}$没有达到停止准则 $\text{do}$

• 从训练集$\mathcal{D}$中采集出包含$k$个样本的小批量：$\{(x^{(i)},y^{(i)}){\}}_{i=1}^k$

• 计算临时的超前参数$\hat{\theta }$：
  $$\hat{\theta }\Leftarrow \theta +\gamma \cdot m$$

• 使用超前参数$\hat{\theta }$计算对应位置的梯度信息：
  $$\mathcal{G}\Leftarrow \frac{1}{k}\sum _{i=1}^k{\nabla }_{\theta }\mathcal{L}[f(x^{(i)};\hat{\theta }),y^{(i)}]$$

• 使用$\mathcal{R}$通过指数加权移动平均法对梯度内积$\mathcal{G}\odot \mathcal{G}$进行累积：
  $$\mathcal{R}\Leftarrow \beta \cdot \mathcal{R}+(1-\beta )\cdot \mathcal{G}\odot \mathcal{G}$$

• 计算动量更新：

  • 需要注意的点：通过历史动量与超前梯度更新当前迭代步骤动量$m$的同时，超前梯度$\mathcal{G}$自身也在被累积梯度优化的学习率更新;
  • 超参数$ϵ$消失了，虽然不知道为什么~
    $$m\Leftarrow \gamma \cdot m-\frac{\eta }{\sqrt{\mathcal{R}}}\odot \mathcal{G}$$

• 计算参数$\theta$更新：
  $$\theta \Leftarrow \theta +m$$

• $\text{End While}$

基于Nesterov动量的RMSProp示例代码

依然使用凸函数$f(x)=x^T\mathcal{Q}x;x=(x_1,x_2{)}^T;\mathcal{Q}=\left(\begin{array}{c}0.50\\ 020\end{array}\right)$作为目标函数，观察其迭代过程。对应代码表示如下：

import numpy as np
import math
import matplotlib.pyplot as plt
from tqdm import tqdm

def f(x, y):
    return 0.5 * (x ** 2) + 20 * (y ** 2)

def ConTourFunction(x, Contour):
    return math.sqrt(0.05 * (Contour - (0.5 * (x ** 2))))

def Derfx(x):
    return x

def Derfy(y):
    return 40 * y

def DrawBackGround():
    ContourList = [0.2, 1.0, 4.0, 8.0, 16.0, 32.0]
    LimitParameter = 0.0001
    for Contour in ContourList:
        # 设置范围时，需要满足x的定义域描述。
        x = np.linspace(-1 * math.sqrt(2 * Contour) + LimitParameter, math.sqrt(2 * Contour) - LimitParameter, 200)
        y1 = [ConTourFunction(i, Contour) for i in x]
        y2 = [-1 * j for j in y1]
        plt.plot(x, y1, '--', c="tab:blue")
        plt.plot(x, y2, '--', c="tab:blue")

def Process():
    Start = (8.0, 1.0)
    StartMomentum = (0.0, 0.0)
    LocList = list()
    LocList.append(Start)
    # 学习率;
    Eta = 0.1
    # Beta指RMSProp加权方法的参数;
    Beta = 0.8
    # Nesterov计算超前位置的参数以及Momentum加权方法的参数;
    alpha = 0.1
    R = 0.0
    Delta = 0.5

    while True:
        SpeedUpStart = (Start[0] + alpha * StartMomentum[0],Start[1] + alpha * StartMomentum[1])
        SpeedUpGradient = (Derfx(SpeedUpStart[0]),Derfy(SpeedUpStart[1]))
        SpeedUpInnerProduct = (SpeedUpGradient[0] ** 2) + (SpeedUpGradient[1] ** 2)

        # 累积梯度
        DecayR = R * Beta
        R = DecayR + ((1.0 - Beta) * SpeedUpInnerProduct)

        # 梯度大小(学习率)更新
        UpdateEta = -1 * (Eta / (math.sqrt(R)))
        UpdateMomentum = (alpha * StartMomentum[0] + UpdateEta * SpeedUpGradient[0],
                          alpha * StartMomentum[0] + UpdateEta * SpeedUpGradient[1])
        Next = (Start[0] + UpdateMomentum[0],Start[1] + UpdateMomentum[1])
        DerNext = (Derfx(Next[0]),Derfy(Next[1]))

        # 使用更新点梯度向量的模 < Delta作为停止准则(因为该函数存在唯一全局最优解,其梯度向量是零向量);
        if math.sqrt((DerNext[0] ** 2) + (DerNext[1] ** 2)) < Delta:
            break
        else:
            LocList.append(Next)
            StartMomentum = UpdateMomentum
            Start = Next
    return LocList

def DrawPicture():
    NesterovRMSPropLocList = Process()
    plt.figure(figsize=(10,5))
    NesterovRMSPropplotList = list()
    DrawBackGround()
    for (x, y) in tqdm(NesterovRMSPropLocList):
        NesterovRMSPropplotList.append((x, y))
        plt.scatter(x, y, s=30, facecolor="none", edgecolors="tab:red", marker='o')
        if len(NesterovRMSPropplotList) < 2:
            continue
        else:
            plt.plot([NesterovRMSPropplotList[0][0], NesterovRMSPropplotList[1][0]], [NesterovRMSPropplotList[0][1], NesterovRMSPropplotList[1][1]], c="tab:red")
            NesterovRMSPropplotList.pop(0)
    plt.show()

if __name__ == '__main__':
    DrawPicture()

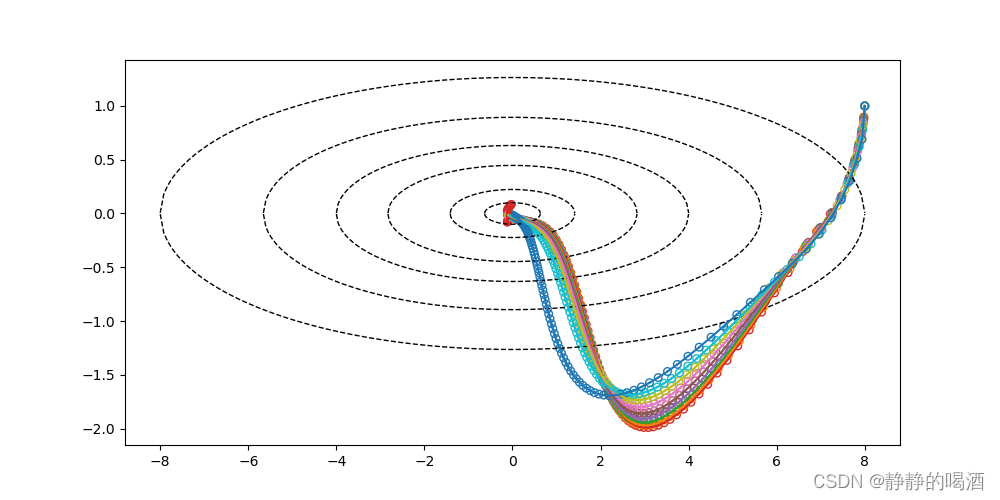
对应图像结果表示如下：

这看起来与$\text{RMSProp}$的图像结果没什么区别~原因在于：我们设置的动量参数alpha过小，从而依赖过去梯度信息的比例过小。可以固定学习率Eta以及$\text{RMSProp}$加权参数Beta，对动量参数alpha$\in [0,1)$进行调整。对应图像表示如下。其中蓝色线表示alpha=0.9时的路径结果；而红色线表示alpha=0.1时的路径结果。
下图是Eta=0.1,beta=0.8时，各alpha对应的路径效果。

同理，我们同样可以固定动量参数alpha和学习率Eta，来观察$\text{RMSProp}$加权参数Beta对迭代路径的影响：
下图是Eta=0.1，alpha=0.9时，各Beta对应的路径效果。

$\text{Reference}$：
《深度学习(花书)》$\text{P189 8.5.2 RMSProp}$