如下图所示,当 θ 不变, ρ 增大为 ρ + Δ ρ ( 即 ρ 1 ) 时 \theta不变,\rho增大为\rho + \Delta \rho(即\rho_1)时 θ不变,ρ增大为ρ+Δρ(即ρ1)时, 面积的增量为:
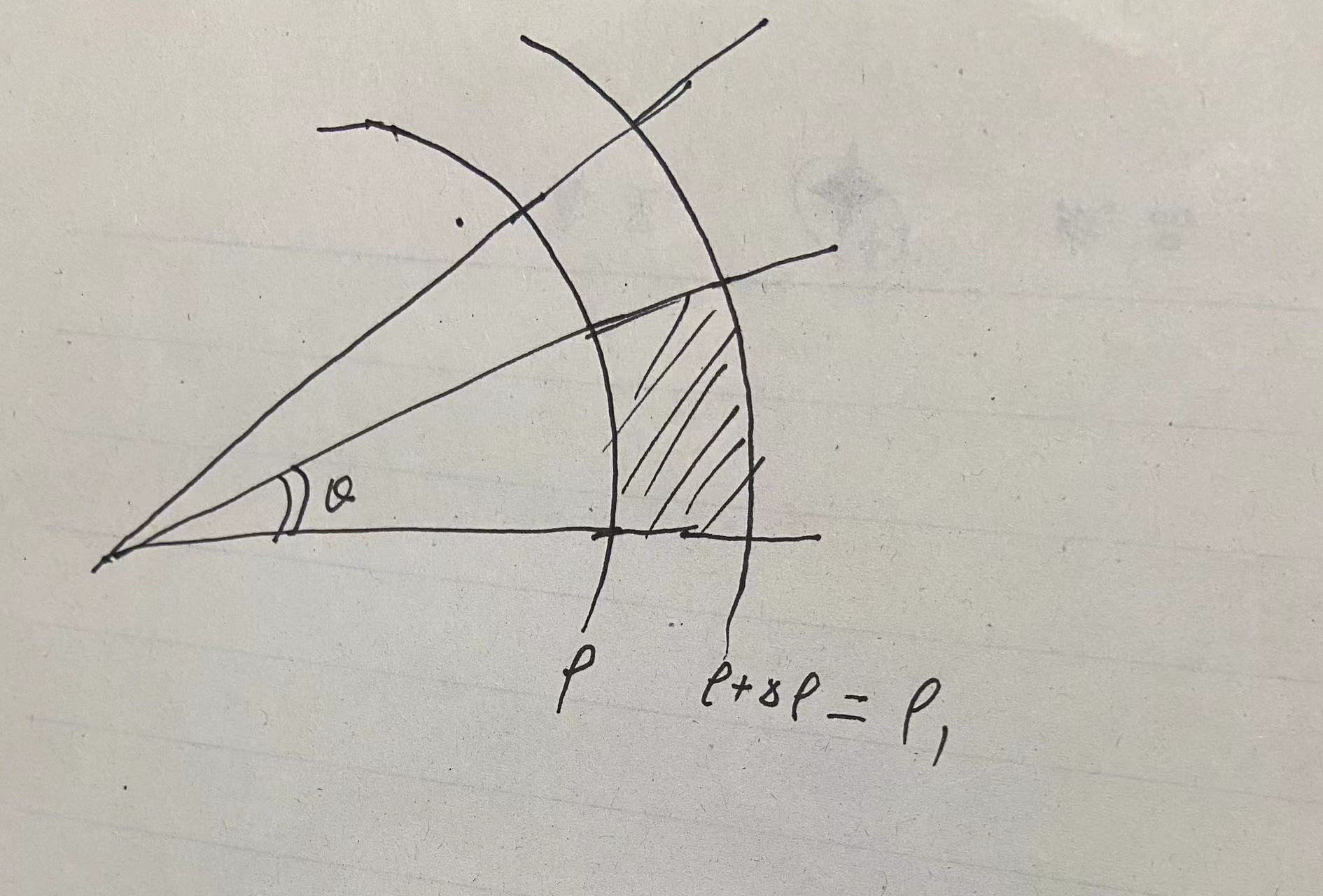
1 2 θ ( ρ + Δ ρ ) 2 − 1 2 θ ρ 2 = θ ρ Δ ρ + 1 2 θ ( Δ ρ ) 2 = 1 2 θ ( 2 ρ + Δ ρ ) Δ ρ = 1 2 ( ρ + Δ ρ + ρ ) Δ ρ θ = 1 2 ( ρ 1 + ρ ) Δ ρ θ \frac{1}{2} \theta (\rho + \Delta \rho )^2 - \frac{1}{2}\theta \rho^2 = \\ \theta \rho \Delta \rho+\frac{1}{2}\theta (\Delta \rho)^2=\\ \frac{1}{2}\theta(2\rho+\Delta \rho)\Delta \rho = \frac{1}{2}(\rho+\Delta \rho + \rho)\Delta \rho \theta = \\ \frac{1}{2}(\rho_1+ \rho)\Delta \rho \theta 21θ(ρ+Δρ)2−21θρ2=θρΔρ+21θ(Δρ)2=21θ(2ρ+Δρ)Δρ=21(ρ+Δρ+ρ)Δρθ=21(ρ1+ρ)Δρθ
因此二重积分:
∫ y 1 y 2 ∫ x 1 x 2 f ( x , y ) d x d y = ∫ θ 1 θ 2 ∫ ρ 0 ρ 1 f ( ρ cos θ , ρ sin θ ) ρ d ρ d θ \int_{y_1}^{y_2} \int_{x_1}^{x_2} f(x,y)dx dy = \int_{\theta_1}^{\theta_2} \int_{\rho_0}^{\rho_1} f(\rho\cos \theta,\rho \sin \theta) \rho d\rho d \theta ∫y1y2∫x1x2f(x,y)dxdy=∫θ1θ2∫ρ0ρ1f(ρcosθ,ρsinθ)ρdρdθ