一、实验目的
(1)学习并掌握常见的机器学习方法;
(2)能够结合所学的python知识实现机器学习算法;
(3)能够用所学的机器学习算法解决实际问题。
二、实验内容与要求
(1)掌握神经网络的基本原理,掌握并理解反向传播算法;
(2)能够结合单层神经网络实现分类问题;
(3)根据所提供的代码,完成基本的分类问题的代码;
(4)能够正确输出结果
三、实验过程及代码
3.1搭建神经网络
(1)初始化每层节点数量
假设W1为输入层到隐层的权重数组、b1为输入层到隐层的偏置数组;W2为隐层到输出层的权重数组,b2为隐层到输出层的偏置数组。
| def layer_sizes(X, Y, n_h = 4): n_x = X.shape[0] #输入层 n_h = n_h#,隐藏层 n_y = Y.shape[0] #输出层
return (n_x,n_h,n_y) |
(2)初始化每层参数
其中对权值的初始化我们利用了numpy中的生成随机数的模块np.random.
randn,偏置的初始化则使用了np.zero模块。通过设置一个字典进行封装并返回包含初始化参数之后的结果。
| def initialize_parameters( n_x , n_h ,n_y): #Please add something np.random.seed(2) w1 = np.random.randn(n_h,n_x)*0.01 b1 = np.zeros((n_h,1)) w2 = np.random.randn(n_y,n_h)*0.01 b2 = np.zeros((n_y,1)) parameters = { 'w1':w1, 'w2': w2, 'b1': b1, 'b2': b2, } return parameters |
(3)前向传播
在定义好网络结构并初始化参数完成之后,就要开始执行神经网络的训练过程了。而训练的第一步则是执行前向传播计算。假设隐层的激活函数为 tanh函数,输出层的激活函数为sigmoid函数。
| def forward_propagation( X , parameters ): #Please add something w1 = parameters['w1']#4*2 b1 = parameters['b1']#4*1 w2 = parameters['w2']#1*4 b2 = parameters['b2']#1*1 Z1 = np.dot(w1,X)+b1#4*400 A1 = np.tanh(Z1)#4*400 Z2 = np.dot(w2,A1)+b2#1*400 A2 = sigmoid(Z2)#1*400 cache = { "Z1":Z1, "A1": A1, "Z2": Z2, "A2": A2 } return cache |
(4)计算交叉熵成本
| def compute_cost(A2,Y): """ 计算交叉熵成本,
参数: A2 - 使用sigmoid()函数计算的第二次激活后的数值 Y - "True"标签向量,维度为(1,数量)
返回: 成本 - 交叉熵成本 """ #Please add something m = Y.shape[1] first = np.multiply(-Y,np.log(A2)) second = np.multiply(1-Y,np.log(1-A2)) cost = np.sum(first-second)/m return cost |
(5)搭建反向传播函数
当前向传播和当前损失确定之后,就需要继续执行反向传播过程来调整权值了。中间涉及到各个参数的梯度计算,具体如下所示:
| def backward_propagation(parameters,cache,X,Y): #Please add something m = X.shape[1] w1 = parameters['w1']#4*2 w2 = parameters['w2']#1*4 A1 = cache['A1']#4*400 A2 = cache['A2']#1*400 dz2 = A2-Y#1*400 dw2 = (1/m)*np.dot(dz2,A1.T)#1*4 db2 = (1/m)*np.sum(dz2,axis = 1,keepdims = True)#1*1 #最难理解的部分 dz1 = np.multiply(np.dot(w2.T,dz2),1-np.power(A1,2))#4*400 dw1 = (1/m)*np.dot(dz1,X.T)#4*2 db1 = (1/m)*np.sum(dz1,axis = 1,keepdims = True)#4*1 grads = { 'dw1':dw1, 'db1': db1, 'dw2': dw2, 'db2': db2, } return grads |
(6)根据梯度下降更新规则更新参数
当前向传播和当前损失确定之后,就需要继续执行反向传播过程来调整权值和偏值了。这里涉及到了梯度下降算法,具体的公式步骤如下:

| def update_parameters(parameters,grads,learning_rate=0.1): #Please add something w1 = parameters['w1'] w2 = parameters['w2'] b1 = parameters['b1'] b2 = parameters['b2'] dw2 = grads['dw2'] dw1 = grads['dw1'] db2 = grads['db2'] db1 = grads['db1'] w2 = w2 - learning_rate*dw2 b2 = b2 - learning_rate * db2 w1 = w1 - learning_rate * dw1 b1 = b1 - learning_rate * db1 parameters = { 'w1': w1, 'w2': w2, 'b1': b1, 'b2': b2, } return parameters |
(7)整合模型
| def nn_model(X,Y,n_h,num_iterations,print_cost=False): #Please add something np.random.seed(3) n_x = layer_sizes(X,Y)[0] n_y = layer_sizes(X,Y)[2] parameters = initialize_parameters(n_x,n_h,n_y) w1 = parameters['w1'] w2 = parameters['w2'] b1 = parameters['b1'] b2 = parameters['b2'] for i in range(num_iterations): cache = forward_propagation(X,parameters) cost = compute_cost(cache["A2"],Y) grads = backward_propagation(parameters,cache,X,Y) parameters = update_parameters(parameters,grads,learning_rate=0.5) if print_cost: if i%100==0: print("第",i,"次循环,成本为"+str(cost)) return parameters |
3.2模型预测
(1)预测代码
| def predict(parameters,X): """ 使用学习的参数,为X中的每个示例预测一个类
参数: parameters - 包含参数的字典类型的变量。 X - 输入数据(n_x,m)
返回 predictions - 模型预测的向量(红色:0 /蓝色:1)
""" cache = forward_propagation(X,parameters) predictions = np.round(cache["A2"])
return predictions X,Y = load_planar_dataset() parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True) #绘制边界 plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y) plt.title("Decision Boundary for hidden layer size " + str(4)) predictions = predict(parameters, X) |
(2)预测数据结果

(3)更改隐藏层节点数量
| plt.figure(figsize=(16, 32)) hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50] #隐藏层数量 for i, n_h in enumerate(hidden_layer_sizes): plt.subplot(5, 2, i + 1) plt.title('Hidden Layer of size %d' % n_h) parameters = nn_model(X, Y, n_h, num_iterations=5000) plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y) predictions = predict(parameters, X) accuracy = sklearn.metrics.accuracy_score(predictions.T,Y.T)*100 print ("隐藏层的节点数量: {} ,准确率: {} %".format(n_h, accuracy)) |
(4)输出结果
| 隐藏层的节点数量: 1 ,准确率: 67.25 % 隐藏层的节点数量: 2 ,准确率: 66.5 % 隐藏层的节点数量: 3 ,准确率: 89.25 % 隐藏层的节点数量: 4 ,准确率: 90.0 % 隐藏层的节点数量: 5 ,准确率: 89.75 % 隐藏层的节点数量: 20 ,准确率: 90.0 % 隐藏层的节点数量: 50 ,准确率: 89.75 % |
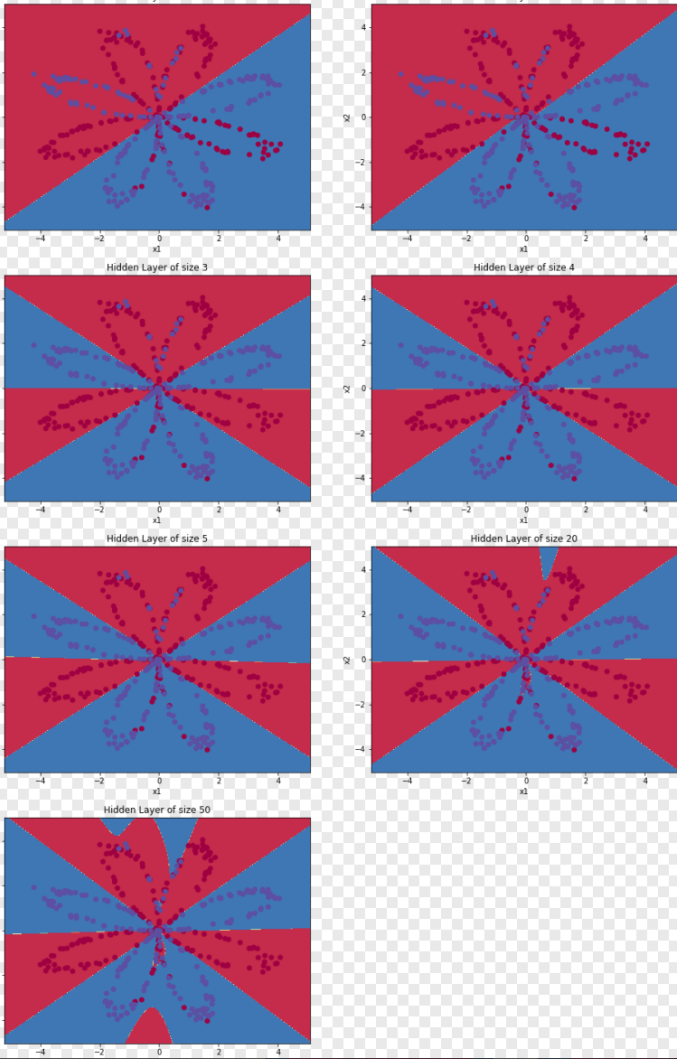
四、实验分析及总结
从上图可以看出,隐藏节点数的增加,可以降低网络误差,提高精准度,但是也会使得网络复杂化,从而增加了网络的训练时间和出现”过拟合”的倾向。
神经网络是一种模拟人脑的神经网络以期能够实现类人工智能的机器学习技术。人脑中的神经网络是一个非常复杂的组织。成人的大脑中估计有1000亿个神经元之多。神经元模型是一个包含输入,输出与计算功能的模型。输入可以类比为神经元的树突,而输出可以类比为神经元的轴突,计算则可以类比为细胞核。把需要计算的层次称之为“计算层”,并把拥有一个计算层的网络称之为“单层神经网络”。有一些文献会按照网络拥有的层数来命名,例如把“感知器”称为两层神经网络。
在神经网络中,隐藏层点数的选择对建立神经网络模型的影响很大,而且是训练时出现“过拟合”的直接原因。我通过了解得知隐层节点数的计算公式都是针对训练样本任意多的情况,而且多数是针对最不利的情况,一般工程实践中很难满足,不宜采用。为了避免过拟合的现象,保证足够高的网络性能和泛化能力,在满足精度要求的前提下取尽可能紧凑的结构,即取尽可能少的隐层节点数 。隐藏层节点数不仅与输入输出层的节点数有关,更与需要解决的问题的复杂度和转换函数的模型以及样本数据的特性等因素有关。确定隐藏层的节点数满足条件有:(1)隐藏层必须小于N-1(2)训练样本必须多于网络模型的连接权数,一般为2-10倍。因此得到,输入层的节点数(变量数)必须小于N-1,合理隐藏层节点数应在综合考虑网络结构复杂程度和误差的情况下节点删除法和扩张法确定。当隐藏节点越多,层数越多时,权值成倍的增长。权值的增长意味着对应的空间的维数越高,过高的维数易导致训练后期的过拟合。当网络的训练次数过多时,可能会出现过拟合的情况。解决过拟合主要两种方法:一种是使用权值衰减的方式,即每次迭代过程中以某个较小的因子降低每个权值;另一种方法就是使用验证集的方式来找出使得验证集误差最小的权值,对训练集较小时可以使用交叉验证等。