54.给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
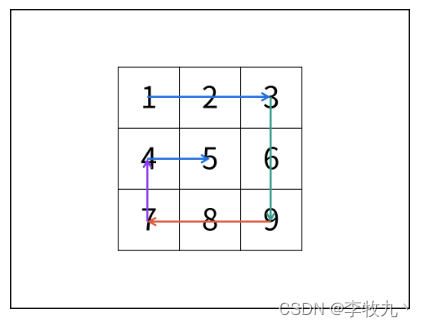
螺旋遍历：从左上角开始，按照 向右、向下、向左、向上 的顺序 依次 提取元素，然后再进入内部一层重复相同的步骤，直到提取完所有元素
示例 1：
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
示例 2：
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

• 我的原始人解法：根据题意设置一个包含四个方向的数组，起点为 (0,0)，当在某个方向移动到超出边界或移动到已到达过的点就转向，如果转向后下一轮移动还是越界或处于已到达点，那就说明结束了螺旋遍历。

•   int m,n;
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();
        m = matrix.length;
        if(m==0)return ans; 
        n = matrix[0].length;
        // 右，下，左，上
        int[][] pos = new int[][]{{0,1},{1,0},{0,-1},{-1,0}};
        // 是否到达过某个点
        int[][] visited = new int[m][n];
        // 当前方向
        int pi = 0;
        // 当前位于坐标
        int i=0,j=0;
        while(true){
        	// 越界或处于已到达点，结束遍历
            if(!isValid(i,j) || visited[i][j]==1)break;
            // 记录当前点
            ans.add(matrix[i][j]);
            visited[i][j]=1;
            int px = pos[pi][0];
            int py = pos[pi][1];
            // 如果按照当前方向移动不可行就转向
            if(!isValid(i+px,j+py) || visited[i+px][j+py]==1){
                pi=(pi+1)%4;
                px = pos[pi][0];
                py = pos[pi][1];
            }
            // 更新坐标
            i+=px;
            j+=py;
            
        }
        return ans;
    }
    public boolean isValid(int i,int j){
        return i>=0 && i<m && j>=0 && j<n;
    }
  

• 他人题解：由于螺旋打印其实就是四个方向上的不断向内收缩，所以我们可以用四个变量 t(top),b(bottom),l(left),r(right) 来表示上下左右的边界，模拟一圈打印，你会发现，最开始顶部的从左到右，就是固定 t，从 l 到 r 遍历，第一行遍历完就需要收缩顶部，即 t+1；然后是最右侧的从上到下，其实就是固定 r，从 t 到 b 遍历，遍历完最右侧，右侧往里收缩，即 r - 1…，只要 l > r 或 t > b 就表示已经收缩到极点开始反向扩张了，就退出遍历。
  

•   public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();
        int m = matrix.length;
        if(m==0)return ans; 
        int n = matrix[0].length;
        int t = 0, b = m - 1, l = 0, r = n - 1;
        while(true){
            for(int i=l;i<=r;i++)ans.add(matrix[t][i]);
            if(++t>b)break;
            for(int i=t;i<=b;i++)ans.add(matrix[i][r]);
            if(--r<l)break;
            for(int i=r;i>=l;i--)ans.add(matrix[b][i]);
            if(--b<t)break;
            for(int i=b;i>=t;i--)ans.add(matrix[i][l]);
            if(++l>r)break;
        }
        return ans;
    }