维吉尼亚密码属于多表代换密码

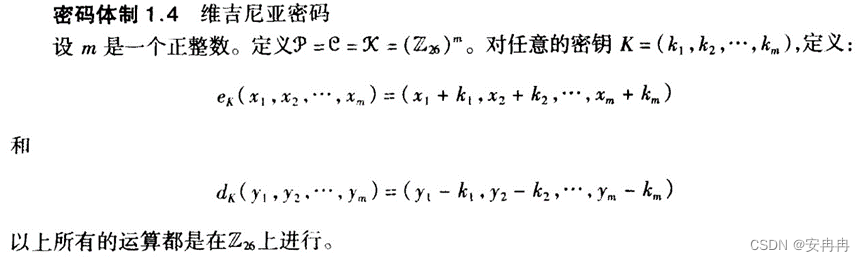
其中A<–>0,B<–>1,…,Z<–>25,则每个密钥K相当于一个长度为m的字母串,称为密钥字。维吉尼亚密码一次加密m个明文字母。
示例:设m=6,密钥字为“CIPHER”,对应数字串K=(2,8,15,7,4,17)。要加密明文为:thiscrypto,则
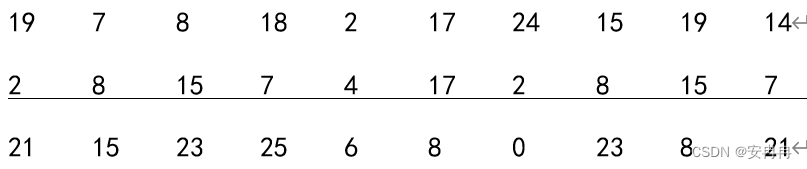 则相应的密文为:VPXZGIAXIV
则相应的密文为:VPXZGIAXIV
解密时,使用相同的密钥字进行逆运算即可。
可以看出,维吉尼亚密码的密钥空间为26^m。
加密:
Plaintext = 'THISCRYPTO'#字母需要大写
K = [2,8,15,7,4,17]
#print(K)#密钥
Ciphertext = ''
for i in range(len(Plaintext)):
M_i = ord(Plaintext[i]) - 65
K_i = K[i%len(K)]
C_i = (M_i+K_i)%26
Ciphertext += chr(C_i+ 65)
print(Ciphertext)
解密:
Ciphertext = 'VPXZGIAXIV'
K = [2,8,15,7,4,17]
Plaintext = ''
for i in range(len(Ciphertext)):
C_i = ord(Ciphertext[i]) -65
K_i = K[i%len(K)]
M_i = (C_i - K_i)%26
Plaintext += chr(M_i+ 65)
print(Plaintext)