蒙特卡洛方法的简单应用

news2024/11/15 8:09:57

蒙特卡洛方法的简单应用

圆周率估算

eastimate pi
python version 3.11
RNG:np.random.random

import os
figure_save_path = "file_fig"
import warnings
warnings.filterwarnings("error")
import numpy as np
np.random.seed(0)
import matplotlib.pyplot as plt
from PIL import Image

def main(times=100):
    print("RNG:", "Python numpy.random.random")
    print("开始估算")
    Nlist = [1000000*i for i in range(1, times)]
    Pilist = []
    Slist  = []
    gif_frames = []

    for i in range(1, times):
        N = Nlist[i-1]
        random_points = np.random.random((2, N))
        radius = sum(random_points[:]**2)
        count = np.sum(radius<=1)
        ave = count/N
        S2 = ((N-count)*ave**2+count*(1-ave)**2)/(N-1)
        S  = S2**0.5 
        Pilist.append(4*ave)    
        Slist.append(4*S/N**0.5)

        plt.xlabel("test_times")
        plt.ylabel("estimate_pi_value", rotation=90)
        plt.title("Estimate Pi")
        plt.errorbar(Nlist[:i], Pilist[:i], Slist[:i], label="estimate pi", c="green")
        plt.axhline(np.pi,label="exact pi", c="red")
        plt.legend()
        if not os.path.exists(figure_save_path):
            os.makedirs(figure_save_path)
        else:
            pass
        plt.savefig(os.path.join(figure_save_path, str(i) + ".jpg"))  
        plt.cla()
     
        img = Image.open(os.path.join(figure_save_path, str(i) + ".jpg"))
        gif_frames.append(img)
    print("估算完成")
    print("开始绘制动画")
    gif_frames[0].save("estimate-pi.gif",
        save_all=True, append_images=gif_frames[1:], duration=200, loop=0)
    print("动画绘制完成")
    
main()
input("press any key to exit")

动画

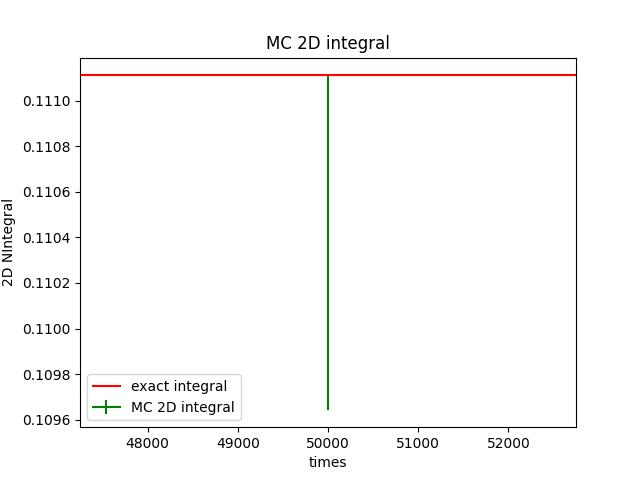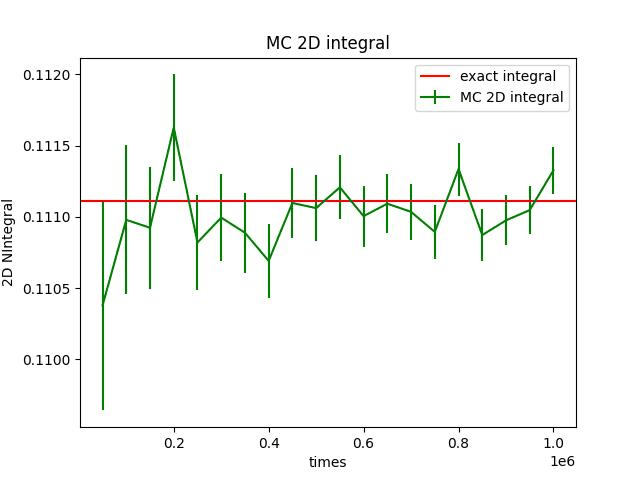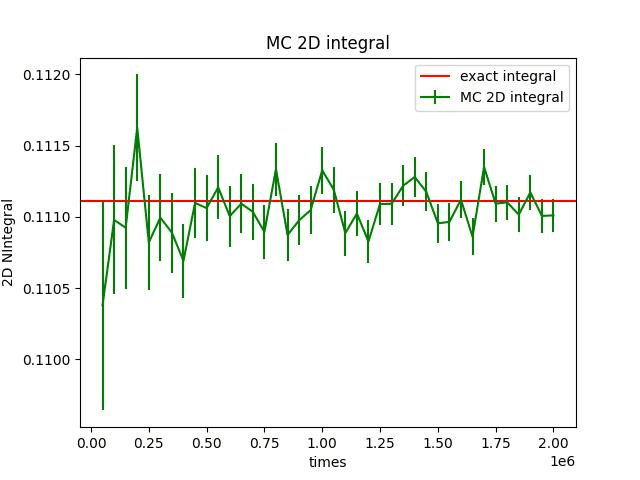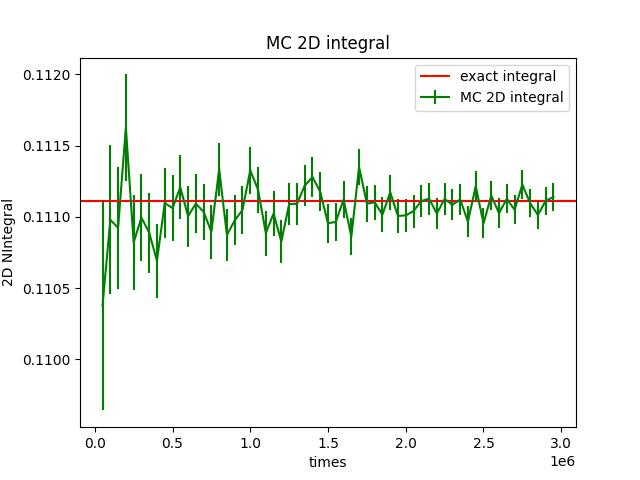
二维积分估算

2dintegral
RNG:numpy.random.random
Python version:3.11
允许积分类型 \int\int f(x,y)dxdy

若实现手动输入方程功能会增加程序解析负担,大约是十倍左右,故不予实现
若需要实现,可以仿照如下例子:

def main(X_start=0, X_end=1, Y_start=0, Y_end=1):
    print("RNG:numpy.random.random")
    print("")
    funstr = input("输入方程")
    #funstr = "x**2*y**2"
    f = lambda x,y: eval(funstr)
    #f = lambda x,y:x**2*y**2
    print("运算开始")
    
    N = 10000
    
    start = time.time()
    random_xpoints = np.random.uniform(X_start, X_end, N)
    random_ypoints = np.random.uniform(Y_start, Y_end, N)

    X = np.arange(X_start, X_end, 100)
    Y = np.arange(Y_start, Y_end, 100)

    guess = np.array(list(map(f, random_xpoints, random_ypoints)))

    ave = sum(guess)/N
    I = ave*(X_end-X_start)*(Y_end-Y_start)

    S2 = sum((guess-ave)**2)/(N-1)
    S  = S2**0.5
    end = time.time()
    
    print(I, "\pm", S/N**0.5)
    print("运算结束,用时:", round(end-start, 4))

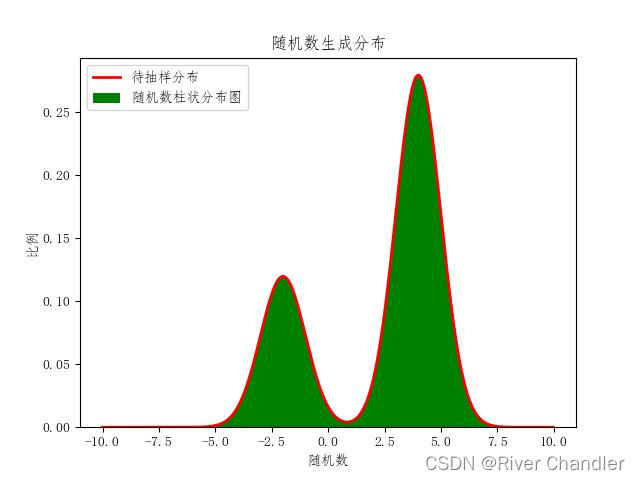
拒绝抽样方法

import os
figure_save_path = "file_fig"
import warnings
warnings.filterwarnings("error")
import numpy as np
np.random.seed(0)
import matplotlib.pyplot as plt
from PIL import Image
from copy import deepcopy

plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False

######
#待抽样分布x~f(x)
#已有分布g(x)
#建议分布c*g(x)
#在概率空间有c*g(x)恒大于f(x)

#step 1 按f(x)抽样 得x,x_i~f(x) x.size 
#step 2 生成u,u_i~U[0, max(c*g(x))] u.size = x.size
#step 3 从x中选取满足u_i<f(x_i)的样本
######

f1 = lambda x:0.3/np.sqrt(np.pi*2)*np.exp(-(x+2)**2/2) +\
              0.7/np.sqrt(np.pi*2)*np.exp(-(x-4)**2/2)

x_start = -10
x_end   =  10

def main(f1=f1, x_start=x_start, x_end=x_end, N = int(1e+7), maxiter = 1000):

    #已有分布为 numpy.random.random 导出的均匀分布
    
    num_wanted  = deepcopy(N)
    result = np.zeros(num_wanted)
    
    has_get_num = 0
    itertimes   = 0
    random_num  = np.zeros(N)
    x           = np.arange(x_start, x_end, 0.01)
    
    if N >= int(1e4):
        N = int(num_wanted /10)
    else:
        pass
    
    while has_get_num < num_wanted:
        itertimes += 1
        if itertimes >= maxiter:
            print("无法生成足够多的随机数")
            break
        else:
            pass

        #拒绝方法：cg(x)<=f(x)        
        sample_try = np.random.random(N)
        sample_try = (x_end - x_start) * sample_try + x_start

        sample_test= f1(sample_try)
        c = 1 + max(f1(x))
        sample_test *= c
        
        sample_help = np.random.random(N) * (max(sample_test)-0) + 0
        
        sample = sample_try[sample_help<sample_test]

        if has_get_num + sample.size > num_wanted:
            result[has_get_num:num_wanted-1] = sample[:num_wanted-has_get_num-1]
        else:
            result[has_get_num:has_get_num+sample.size] = sample

        has_get_num += sample.size

    plt.title("随机数生成分布")
    plt.xlabel("随机数")
    plt.ylabel("比例")
    plt.plot(x, f1(x), color='red', label="待抽样分布", linewidth=2)
    plt.hist(result, bins=200, label="随机数柱状分布图", color='green', density=True)
    plt.legend(prop={'size': 10})
    plt.pause(0.01)
    if not os.path.exists(figure_save_path):
        os.makedirs(figure_save_path)
    else:
        pass
    plt.savefig(os.path.join(figure_save_path, "随机数生成分布" + ".jpg"))
    return result

c = main()