Problem: 1137. 第 N 个泰波那契数

题目解读

首先我们来解读一下本题的意思🔍

• 相信读者在看到【泰波那契数】的时候，不禁会联想到【斐波那契数】，它们呢是一对孪生兄弟，这个 泰波那契数 相当于是 斐波那契数 的加强版
• 我们首先可以来看到这个递推公式Tn+3 = Tn + Tn+1 + Tn+2，读者可能看不太懂，我们将其做一个转换为Tn = Tn-1 + Tn-2 + Tn-3，即把所有n都统一-3。那么第N个泰波那契数就等于前面3个泰波那契数的和

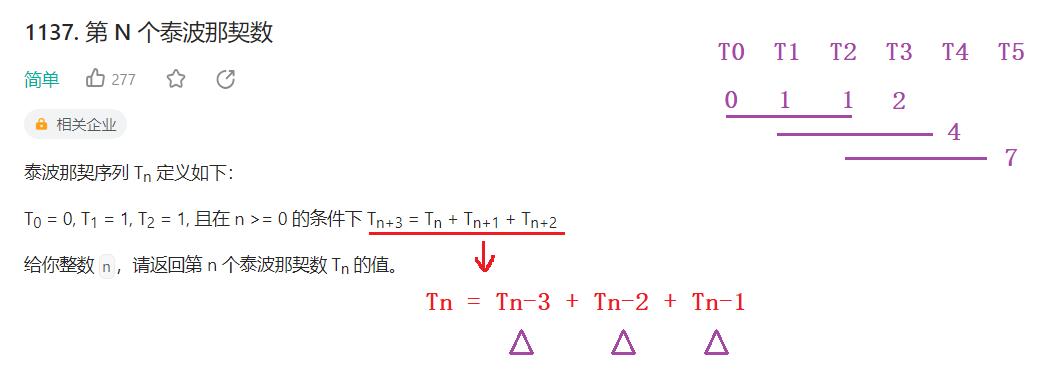
• 看到上面的T3，就是前3个数的和等于2，以此类推T4就是T1 + T2 + T3 = 4

解题方法

看完了上面对于题目的分析之后，下面我将介绍两种解法

dp动态规划

首先的话就是本题需要掌握的重点即【动态规划】的解法，我们要分成五步去求解

1. 状态表示

• 首先读者要清楚的是在求解动态规划的题目时，都是需要一个dp数组的，那么对于【状态表示】的含义就是dp表里的值所表示的含义

那这个状态表示是怎么来的呢？

① 第一个呢就是按照题目要求来，即dp[i]表示的就是第i个泰波那契数列的值

② 第二个呢则是需要读者有丰富的刷题经验，可以读完题目之后就得出对应的结果

③ 第三个呢则是在分析问题的过程中，发现重复的子问题

如果读者之前有接触过类似的动态规划问题的话，就会看到一些题解里讲：这道题的 状态表示 是怎样的，然后就直接讲本题的 状态表示方程，根本没有说这道题的状态表示是怎么来的。这个得来的过程我会在其他动态规划的题目中进行讲解

👉 所以读者在解类似的问题时一定要知道下面的这个【状态表示方程】是怎么来的，做到 “ 知其然，知其所以然 ”

---

2. 状态表示方程

• 那么本题的状态表示方程为dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

3. 初始化

• 在清楚【状态表示方程】该如何写之后，我们要去做的就是对这个dp数组做一个初始化的工作。看到下面的这个dp数组，如果在一开始我们的下标取值就到0的话，那么i - 1、i - 2、i - 3这些就会造成 越界

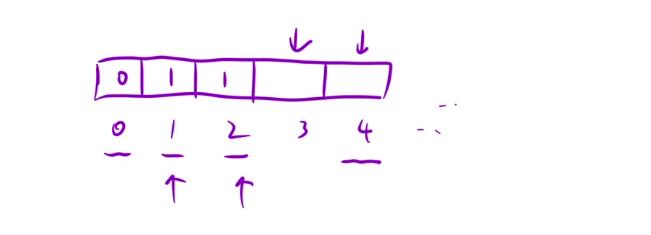
• 因此我们要给这个dp数组去做一个初始化，具体的就是对前三个数据即dp[0]、dp[1]、dp[2]分别初始化为【0】【1】【1】，那我们在后面遍历计算的时候就只需要从下标为3的位置开始即可

 dp[0] = 0, dp[1] = dp[2] = 1;

4. 填表顺序

• 接下去的话就是把dp数组按照 状态表示方程 给填充好即可

for(int i = 3; i <= n; ++i)
{
    // 状态转移方程
    dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}

5. 返回值

• 最后一块我们处理返回值，根据题目要求我们是要返回【第 n 个泰波那契数 Tn 的值】，所以直接 return dp[n] 即可

---

但是呢，若只考虑上面的这一些，在提交的时候是会出现越界的情况，因为在题目中给出的n的范围为[0, 37]，因此对于dp[0]还好说，但对于后面的数据就会出现越界的情况

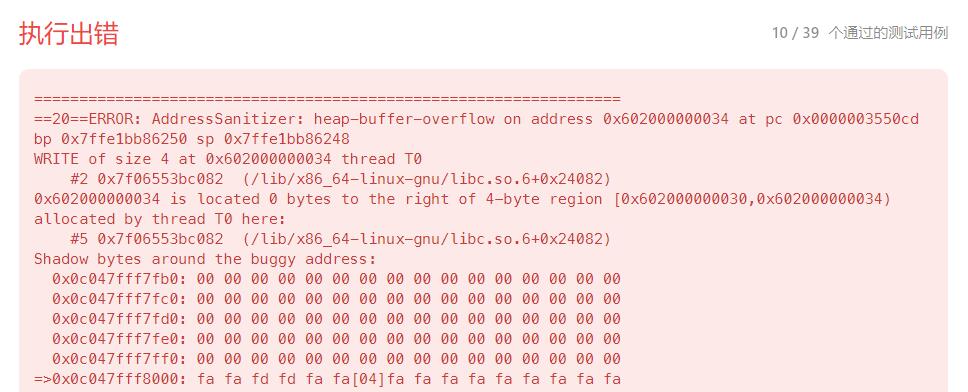
因此我们还需要去考虑一些边界的问题

// 边界问题处理
if(n == 0)  return 0;
if(n == 1 || n == 2)    return 1;

👉 整体代码会在最后给出

迭代优化✔

看完上面这一种，我们再来看看其是否可以去做一个优化

• 如果读者有接触过迭代算法的话，应该很快能想到本题的思路，因为是三个三个去做的累加，所以我们在这里可以定义三个变量a、b、c，它们累加后的值可以放到变量d中

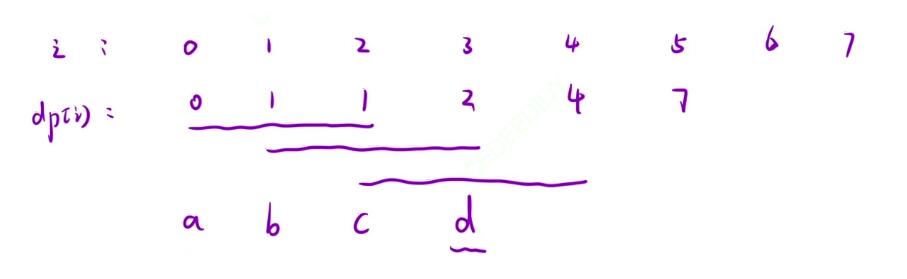
• 因此在累加完一轮之后，我们就需要去做一个迭代的操作

a = b; b = c; c = d;

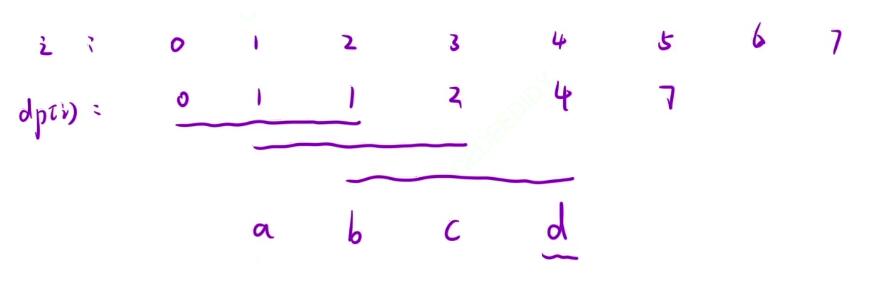
• 那么在最后我们所需要返回的值就是这个d

return d;

复杂度

• 时间复杂度:

对于第一种dp的解法，其时间复杂度为$O(n)$，而对于第二种迭代的解法时间复杂度为$O(1)$

• 空间复杂度:

对于第一种dp的解法，其空间复杂度为$O(n)$，而对于第二种迭代的解法时间复杂度为$O(1)$

👉 所以就这么对比下来迭代优化的方法还是值得大家去掌握的

Code

首先是第一种dp动态规划的解法

class Solution {
public:
    int tribonacci(int n) {
        // 边界问题处理
        if(n == 0)  return 0;
        if(n == 1 || n == 2)    return 1;
        // 1.创建dp表
        vector<int> dp(n + 1);

        // 2.初始化
        dp[0] = 0, dp[1] = 1, dp[2] = 1;

        // 3.填表
        for(int i = 3; i <= n; ++i)
        {
            // 状态转移方程
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        }

        // 4.返回值
        return dp[n];
    }
};

然后的话是第二种利用迭代优化的方法

class Solution {
public:
    // 空间优化
    int tribonacci(int n) {
        // 特殊情况处理
        if(n == 0)  return 0;
        if(n == 1 || n == 2)    return 1;
        int a = 0, b = 1, c = 1, d = 0;
        for(int i = 3; i <= n; ++i)
        {
            d = a + b + c;
            // 迭代
            a = b; b = c; c = d;
        }
        return d;
    }
};