文章目录
- 1. 介绍
- 2. 单层Softmax回归
- 2.1 手写Softmax
- 训练效果
- 2.2 调用pytorch内置的softmax回归层实现
- 调用pytorch内置softmax实验结果
- 总结
- 3. 一层感知机(MLP)+ Softmax
- 实验结果
- Reference
- 写在最后
1. 介绍
在第十节课 多层感知机 的代码实现部分,做的小实验,介绍了对FashionMNIST(衣物)数据集进行十分类的神经网络实现效果,主要展示的是训练的Loss以及准确度的训练批次图,10个epoch
2. 单层Softmax回归
2.1 手写Softmax
Softmax函数,输入是一个二维张量
- 首先,对输入的矩阵进行求指数exp(X) , 不会改变矩阵大小
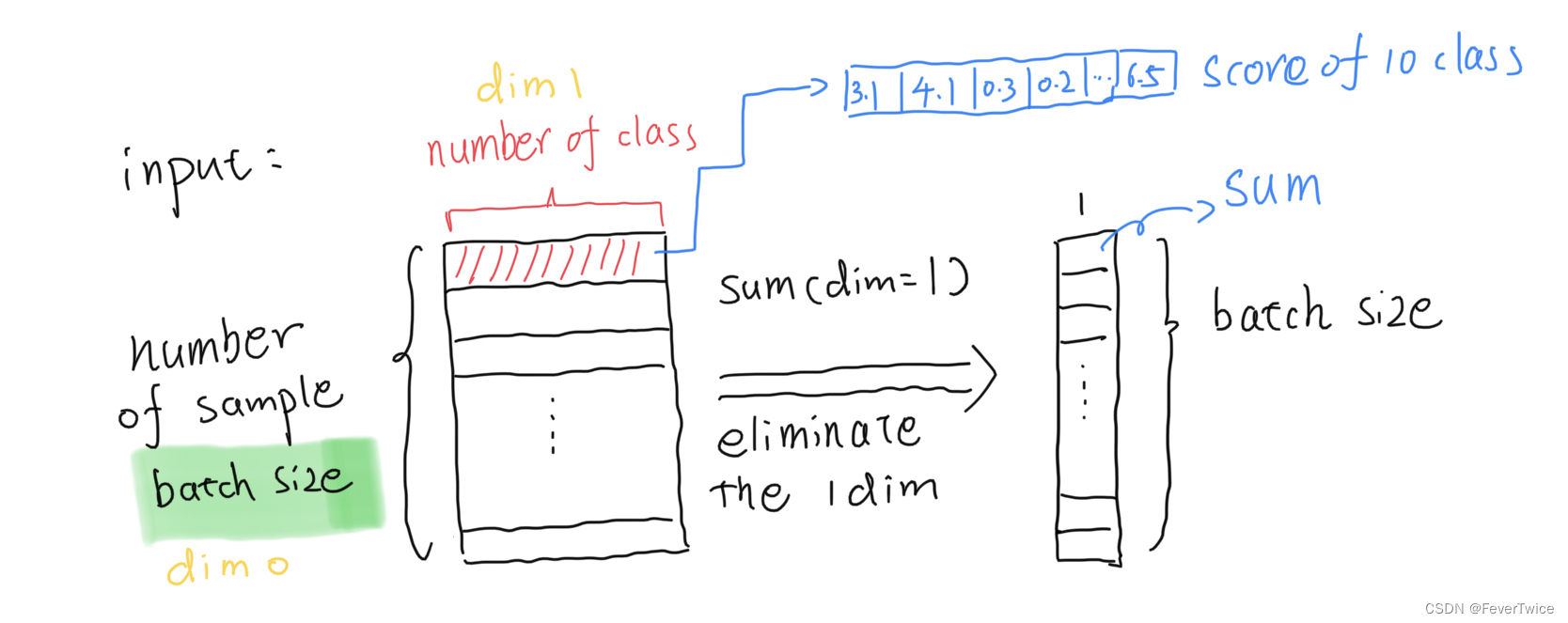
- 接着,对dim_1 进行求和,得到每个example的指数总和(下面公式的分母部分)
- 最后,将整个矩阵相除,得到指数归一化的输出(不改变矩阵形状)
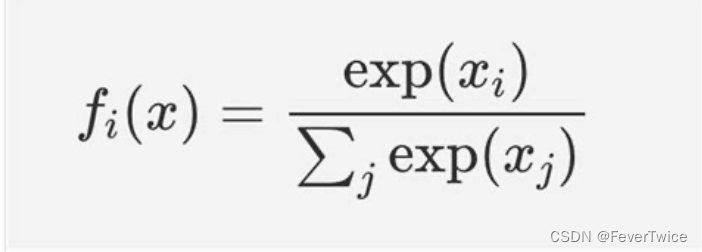
def softmax(X):
X_exp = torch.exp(X) # 1. 求指数
partition = X_exp.sum(1, keepdim=True) # 2. 求和
return X_exp / partition # keepdim to boardcast 3. 输出指数归一化矩阵
这个函数在自定义的网络中net( X )调用
def net(X):
# -1 means convert the dimension atomatically
# the input shape X (256, 1, 28, 28) --> (28*28, 256)
return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
最后,写一个epoch迭代
⚠️:这里面没有写梯度更新的函数,直接调用torch中的自动求道实现,也就是下文代码中的updater.step()。
for X, y in train_iter:
y_hat = net(X) # 将batch传入进去
l = loss(y_hat, y) # 计算loss值
if isinstance(updater, torch.optim.Optimizer):
updater.zero_grad()
l.backward() # 求梯度
updater.step() # 根据梯度更新权重参数矩阵W
metric.add(
float(l) * len(y), accuracy(y_hat, y),
y.size().numel())
else:
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
训练效果
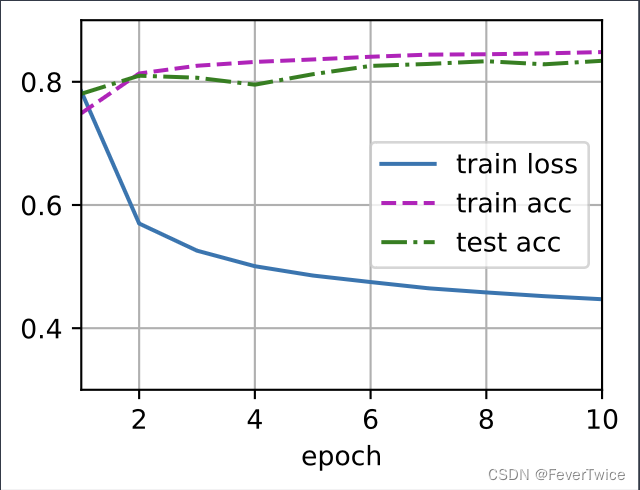
手动实现的Softmax训练效果
2.2 调用pytorch内置的softmax回归层实现
⚠️:nn.CrossEntropyLoss()会在输出的时候自动应用Softmax进行求Loss(公式如下图所示)
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
loss = nn.CrossEntropyLoss() # 损失函数 内嵌了Softmax函数
trainer = torch.optim.SGD(net.parameters(), lr=0.1) # 梯度下降优化器选择
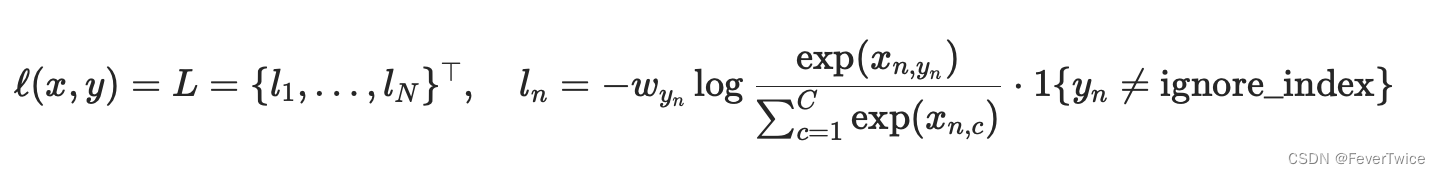
Pytorch文档.CROSSENTROPYLOSS
调用pytorch内置softmax实验结果
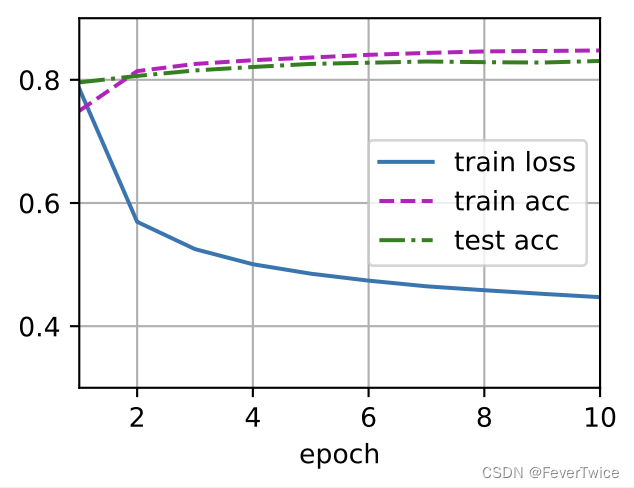
内置Softmax实现10分类的回归效果
总结
可以看到,调用torch内部实现的Softmax函数经过优化之后,相比手写的Softmax函数,迭代的过程更加稳定(抖动更小)
3. 一层感知机(MLP)+ Softmax
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
# function ReLU
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
# model
def net(X):
X = X.reshape((-1, num_inputs)) # 行数自动调整(batch_size),列数规定
H = relu(X @ W1 + b1)
return (H @ W2 + b2)
loss = nn.CrossEntropyLoss() # 隐式实现 Softmax
实验结果
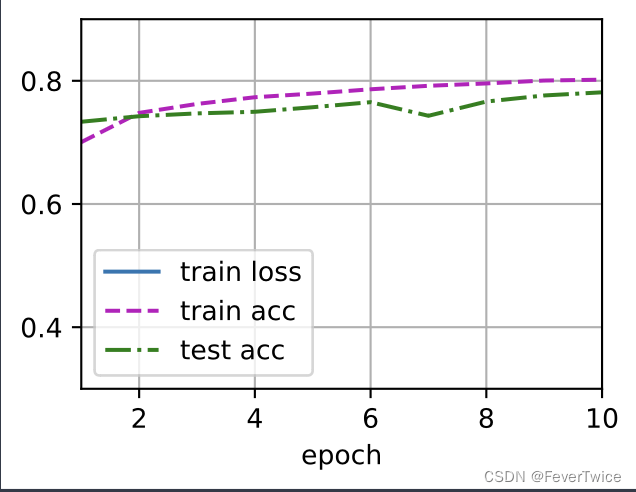
MLP实现的效果跟前面用单层的Softmax实现的效果差不多
Reference
- 李沐老师的课程网站地址 课程网址
- 动手学深度学习B站课程地址
写在最后
各位看官,都看到这里了,麻烦动动手指头给博主来个点赞8,您的支持作者最大的创作动力哟!
才疏学浅,若有纰漏,恳请斧正
本文章仅用于各位作为学习交流之用,不作任何商业用途,若涉及版权问题请速与作者联系,望悉知


![[每周一更]-(第66期):Docker 守护进程说明](https://img-blog.csdnimg.cn/00aed5725b004cf49fd954a48851ba8a.png#pic_center)