算法-DFS+记忆化/动态规划-不同路径 II

1 题目概述

1.1 题目出处

https://leetcode.cn/problems/unique-paths-ii

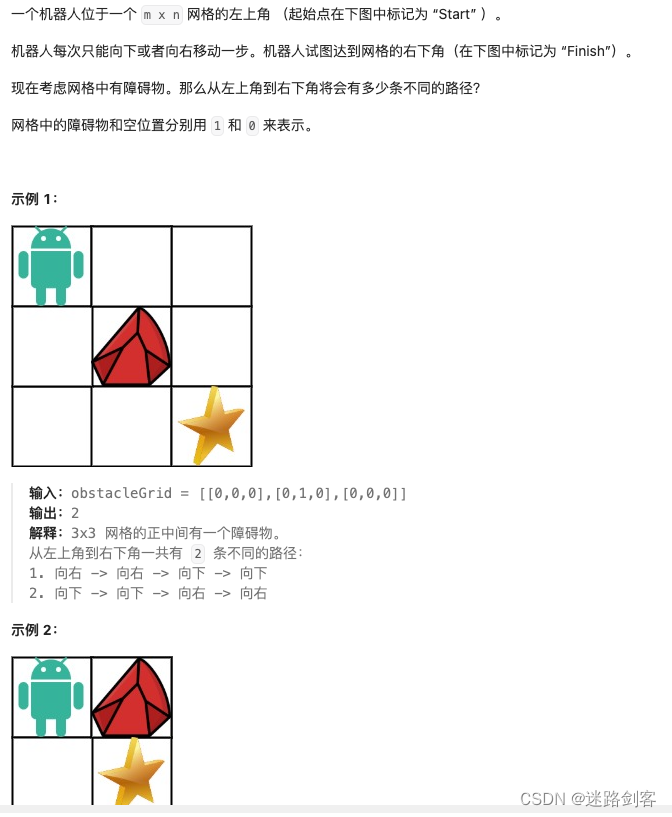
1.2 题目描述

2 DFS+记忆化

2.1 思路

注意题意，每次要么往右，要么往下走，也就是说不能走回头路。但是仍有可能走到之前已经访问过的节点。题意是要求走到终点的路径数，假设往右可以走通，往下也可以走通，那么当前格子的走通方法数 = 往右走通方法数 + 往下走通方法数。

2.2 代码

class Solution {
    int m = 0;
    int n = 0;
    int[][] paths = null;
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        m = obstacleGrid.length;
        n = obstacleGrid[0].length;
        paths = new int[m][n];
        return dfs(obstacleGrid, 0, 0);
    }   

    private int dfs(int[][] obstacleGrid, int i, int j) {
        if (paths[i][j] > 0) {
            return paths[i][j];
        }
        if (obstacleGrid[i][j] == 1) {
            return 0;
        }
        if (i == m - 1 && j == n - 1) {
            paths[i][j] = 1;
            return 1;
        }
        int result = 0;
        if (i < m - 1) {
            result += dfs(obstacleGrid, i + 1, j);
        }
        if (j < n - 1) {
            result += dfs(obstacleGrid, i, j + 1);
        }
        paths[i][j] = result;
        return result;
    }
}

2.3 时间复杂度

O(m*n)

2.4 空间复杂度

O(m*n)

3 二维动态规划

3.1 思路

从上述DFS中思考，可以推出动态规划表达式：dp[i][j] = dp[i+1][j] + dp[i][j+1]。

这里注意两点：

• dp[m-1][n-1] 的值，需要看obstacleGrid[m-1][n-1]是否为1，如果为1代表是障碍，则直接就返回0了。否则就填为1.
• 从动态规划表达式可知，需要i和j都从大到小遍历才可计算。

3.2 代码

class Solution {
    
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        if (n == 0) {
            return 1;
        }
        if (obstacleGrid[m - 1][n - 1] == 1) {
            return 0;
        }
        
        // dp[i][j] = dp[i+1][j] + dp[i][j+1]
        int[][] dp = new int[m][n];
        dp[m-1][n-1] = 1;

        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                if (obstacleGrid[i][j] == 1) {
                    dp[i][j] = 0;
                    continue;
                }
                if (i < m - 1) {
                    dp[i][j] = dp[i+1][j];
                }
                if (j < n - 1) {
                    dp[i][j] += dp[i][j+1];
                }
            }
        }
        
        return dp[0][0];
    }
}

3.3 时间复杂度

O(M*N)

3.4 空间复杂度

O(M*N)

4 一维动态规划

4.1 思路

尝试压缩为一维动态规划。

1. 考虑dp[i][j] = dp[i+1][j] + dp[i][j+1]，那么如果我们每次固定i值，从最后一行的j从大到小递减计算，就能计算出最后一行的各个dp[j]值。
2. 然后i-1到上一行，此时，dp[j]依然表示此行每个位置的通终点方法数，相当于是已经从当前位置累加了往下走的路线的方法数，即dp[i][j] = dp[i+1][j] + dp[i][j+1]中的 dp[i+1][j]，那么我们只需要再计算本行的dp[i][j+1]即可。
3. 综上所述，我们可以压缩二维动态规划为一维动态规划：dp[j] += dp[j+1]

4.2 代码

class Solution {
    
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        if (n == 0) {
            return 1;
        }
        if (obstacleGrid[m - 1][n - 1] == 1) {
            return 0;
        }
        
        int[] dp = new int[n];
        dp[n-1] = 1;

        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                if (obstacleGrid[i][j] == 1) {
                    dp[j] = 0;
                    continue;
                }
                if (j < n - 1) {
                    dp[j] += dp[j+1];
                }
            }
        }
        
        return dp[0];
    }
}

4.3 时间复杂度

3.4 空间复杂度

O(N)