1. 题目解析

LeetCode链接

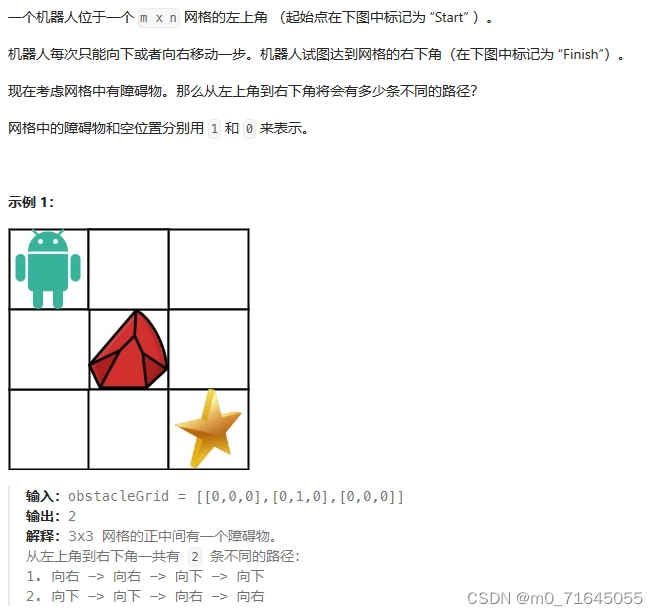
根据题目可以得出，当处于 [i][j] 位置时只能从 [i][j - 1], 和 [i - 1][j] 到达，所以我们只需要将到达上述两点的路径相加就可以得到到达该点的路径和

2. 解题思路

通过分析题目我们可以使用动态规划来解决这道题
首先我们要确定一下状态表示：
由于题目要求的是到达该位置的路径和，所以我们可以用 dp[i][j] 来表示到达 [i, j] 位置时的路径和
然后就是确定状态转移方程：
状态转移方程一般都是从到达该点的最近一步得到
但是由于路径上有障碍物，所以 dp[i][j] 就会分为两种情况：

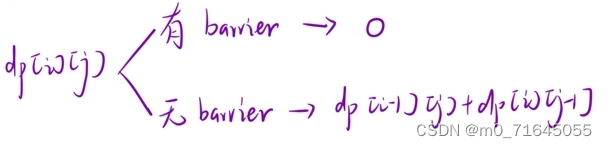
根据上述分析可以得出：
当该点没有障碍物时： dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
当该点没有障碍物时：dp[i][j] = 0
最后是对 dp 数组进行初始化：
在创建虚拟节点时我们需要注意两个问题：

1. 填入的值要保证不影响结果的准确性
2. 要处理好下标的映射关系
   
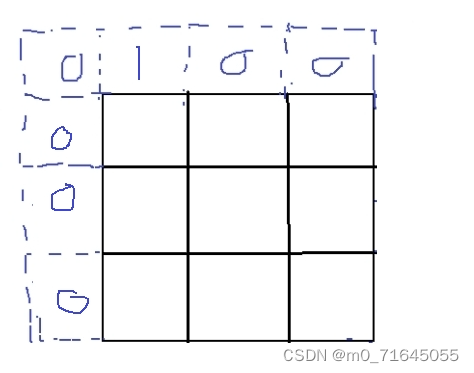
   为了保证结果的准确性我们需要将虚拟节点初始化为 0 ，但是当位于初始节点时也有一种情况所以我们需要将 dp[1][1] 初始化为 1，所以我们可以通过将 dp[0][1] 或者 dp[1][0] 初始化为 1 来到达目的。

3. 代码实现

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
         int[][] dp = new int[m + 1][n + 1];
        dp[0][1] = 1;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (obstacleGrid[i - 1][j - 1] == 1) { 
                    continue;
                }
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

            }
        }
        return dp[m][n];
    }
}