开篇
本文主要介绍在Java中,为什么int类型的最大值为2147483647。
理论值
我们都知道在Java中,int 的长度为32位。
理论上,用二进制表示,32位每一位都是1的话,那么这个数是多少呢?

我们来计算一下,第0位可以用20^00表示,第1位可以用21^11表示,第31位可以用231表示,那么32位二进制能够表示的最大值为232 - 1,所以理论上32位数值的取值范围为0 ~ 232 - 1。
那么,Java的int最大值真的为232 - 1吗?
我们知道,232 - 1这个值为42亿多。而在Java中,int的最大值为2147483647也就是21亿多,为什么有这个差距呢?
分析
我们来看下,Java中int的最大值以及这个最大值的二进制数据。
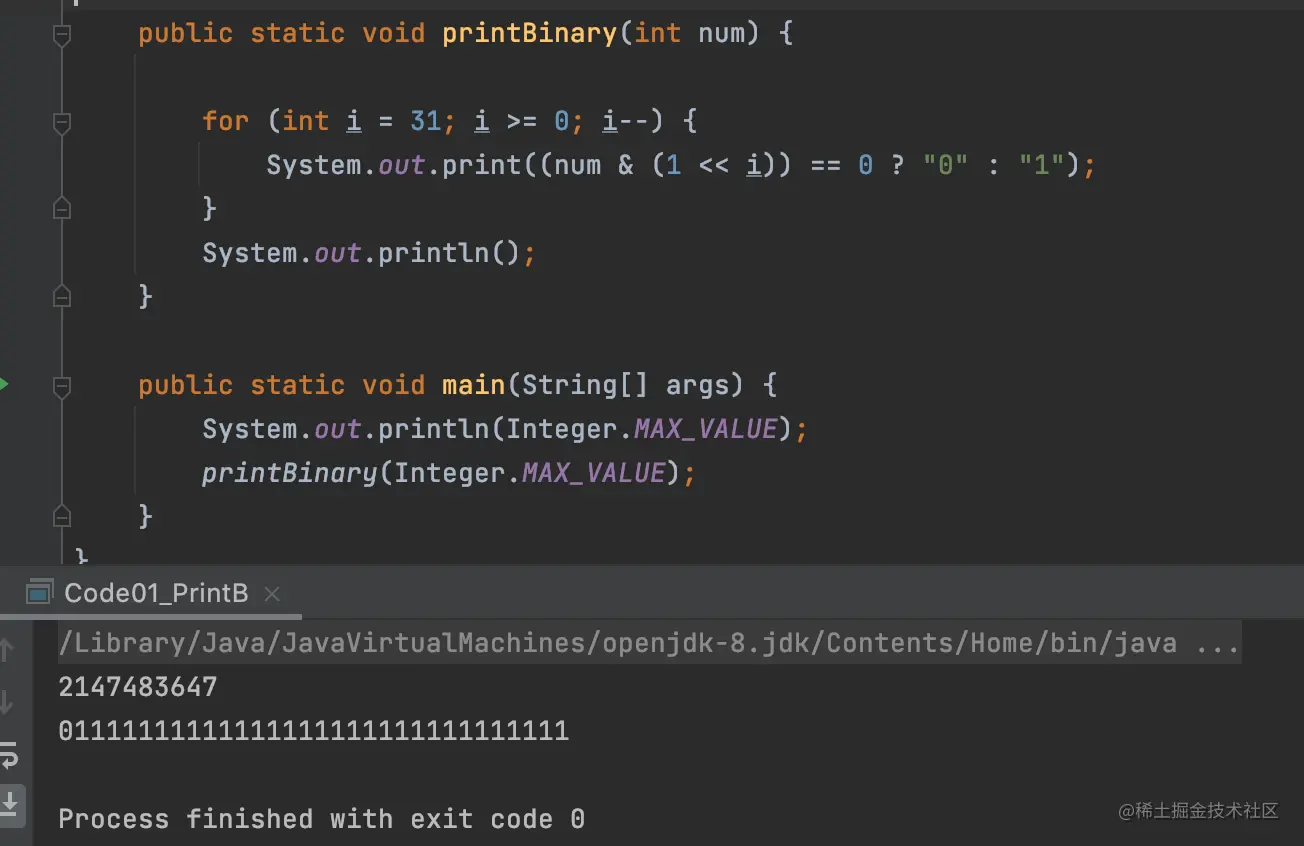
可以看到,int的最大值的最高位为0,而不是1,也就是用31位来表示能够取到的最大值,而不是32位。 因为在Java中,整型是有符号整型,最高位是有特殊含义,代表符号,真正表示数据值的范围为0 ~ 30位。
所以,按照31位来表示的话,其最大值为231 - 1,而这个值就是2147483647即21亿多。
int数据有正负之分,所以最高位用来表示符号,0代表正数,1代表负数。因此Java中,int的数据范围为 -231 ~ 231 - 1。
为啥减1
那为什么都是231, 正数的时候需要减1呢?
我们先来看一下,int的最大值和最小值:

不看符号位的话,最大值比最小值少了1个,这是因为0归到正数里面,所以占用了正数的一个位置。
拓展
负数表示
负数的二进制形式如何表示呢?
先看-100这个数的二进制形式:
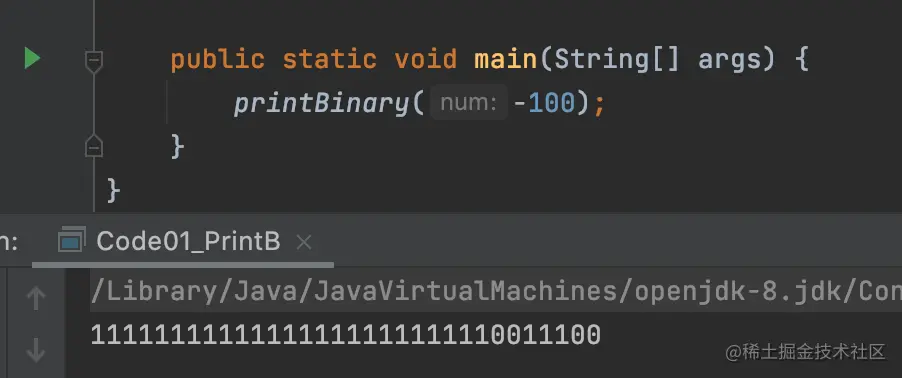
最高位为1,就代表负数。值就为符号位后面的值取反再加上1。

二进制1100100对应的10进制就是100.
反码
反码就是,对一个数的二进制除符号位外,按位取反。取反就是二进制数,1变成0,0变成1,这个过程就是取反。
来看一个例子:

可以看到,a、b两个数的二进制是完全相反的。
为什么要取反加1呢?为什么要设计的这么扭曲?到底是人性的扭曲还是道德的沦丧? 这样设计有什么好处?
在计算机系统里,加减乘除的运算,并不是我们想象中10进制的加减乘除,他最后都会被翻译成2进制的位运算来计算。
假如有2个数,a、b都是整数,那么a + b 对应的二进制就是简单的相加。那么如果a为负数,b为正数呢?在执行a + b 的时候,难道还需要特殊处理一下吗?显然是不可能的,在二进制运算中,加减乘除运算只有各自的一套逻辑,无论符号两边的数是什么样子的。
a为负数,那么对a进行取反加1,再与b进行相加,可以按正常的相加逻辑,这样运算结果依然是正确的,而不是说,当a为负数时,计算机去执行另一套的相加逻辑。设计成取反加1,可以让相加运算不去关注两边的数据是正是负,只执行一套相加逻辑就可以了,这对计算机来说是一个性能的提升。
示例
从上面我们得知,负数的二进制表示为数值部分取反加1,以-100为例,那么可以得出-100 等于 ~100 + 1。

知道负数的二进制的样子后,再看int最小值和-1的二进制数据,就不会惊讶了。要不然,当看到int的最小值的二进制居然是一堆0组成,而-1居然是一堆1,看到这样的数据,心里岂不是冒出一堆问号或者一群小羊飘过。
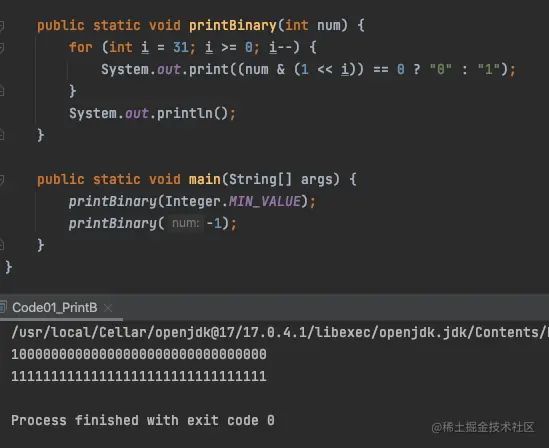
取反加1还是自己的数
有没有一个数,取反加1还是自己?有,0和int的最小值,下面来看下:

先看下Integer.MIN_VALUE的取反加1的过程,可以看到,Integer.MIN_VALUE在取反后加上1,仍然还是他自己。

再看下0的取反加1过程,可以看到0再取反加1后,我嘞个去,居然溢出了!溢出怎么办?溢出就扔了吧不要了,结果还是他自己。

后记
本文主要介绍在Java中,为什么int类型的最大值为什么是21亿多,以及涉及到的知识点的拓展,如有错误欢迎之处。

![[C++]类和对象【下】](https://img-blog.csdnimg.cn/06e475972d404dd694e94b9e2f691978.png)