离散数学 期末复习

图片过多，若无法显示，请转至 https://chenhaotian.top/study/discrete-mathematics-final-review/ 访问全文

发布于 2023-06-18

第 1 章 命题逻辑

1.2 等值演算

真值表法

等值演算法

题：等值演算

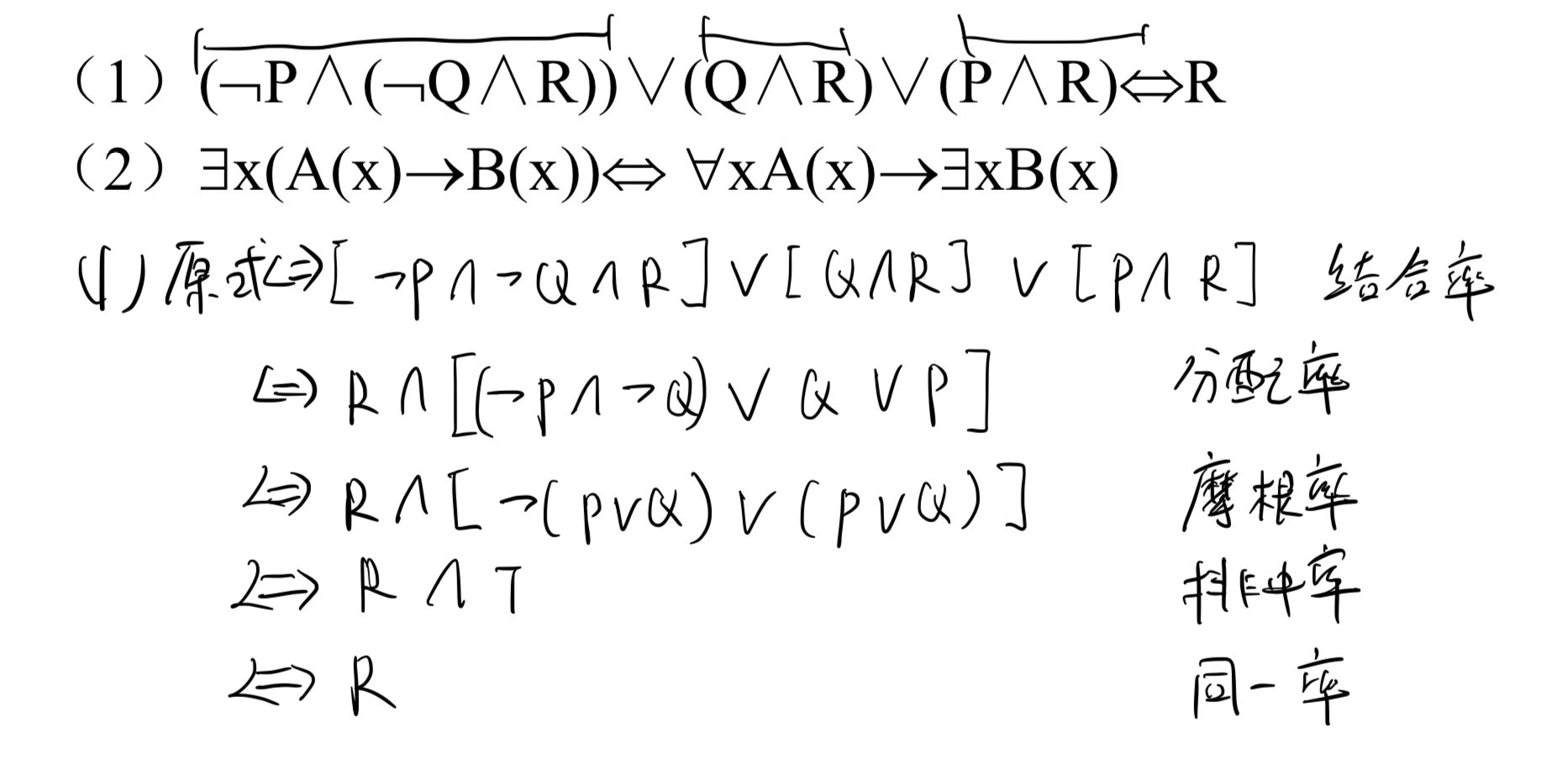
题：等值演算

1.3 范式

由合取式析取起来的式子是析取范式

由析取式合取起来的式子是合取范式

主析取范式和主合取范式互补

主析取范式 主合取范式

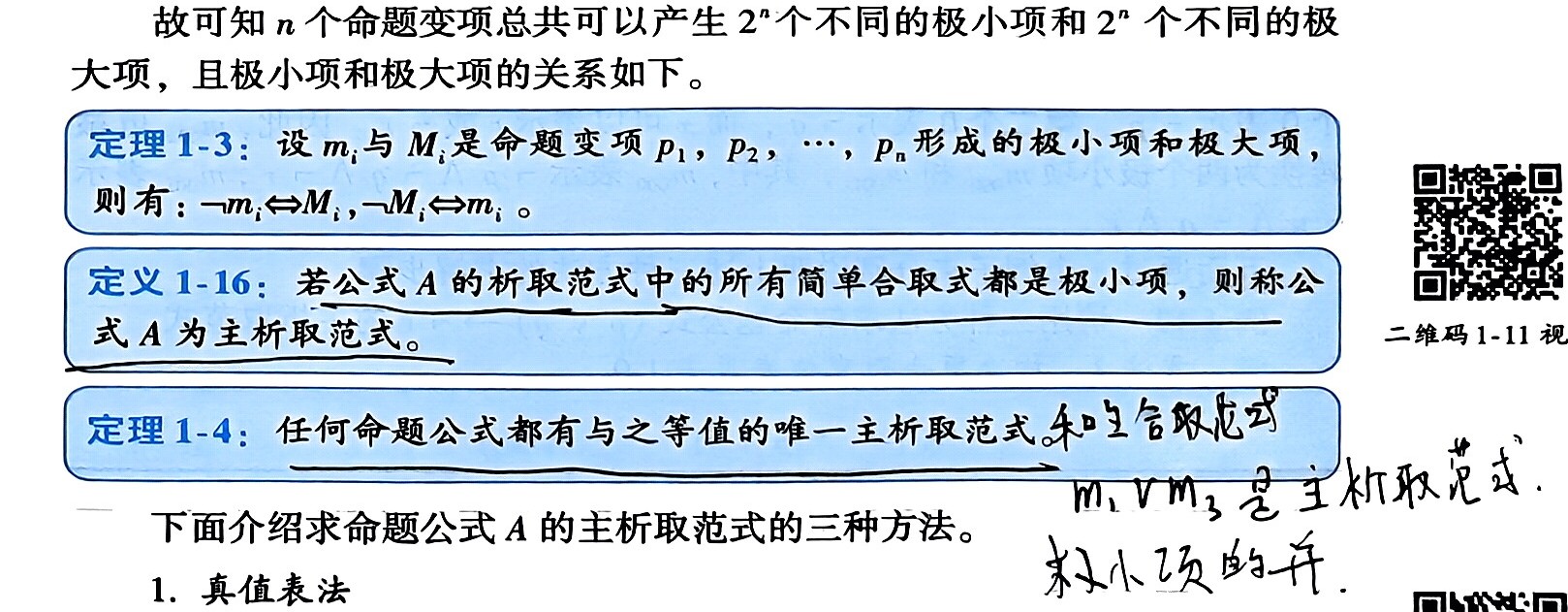
题：主析取范式 主合取范式

主析取范式最好用 $m_x$ 的析取来表示

第 2 章 一阶逻辑

2.1 一阶逻辑概念

个体词 谓词

个体词：个体常项 或 个体变项

个体域：个体词的范围

谓词描述关系

P(x) 或 M(x) 表示一个一元谓词逻辑

量词

量词不能随意调换顺序

量词的优先级比逻辑联结词高

2.2 谓词逻辑解释 分类

辖域 约束变元 自由变元

约束变元换名规则：把指导变元和被指导的约束变元换名

自由变元换名规则：把自由出现的变元换名

解释

题：解释

分类

永真式、永假式、可满足式

2.3 逻辑等值式 前束范式

一阶逻辑等值式

前束范式

题：前束范式

注意运算前先换名

题：消去量词

2.4 逻辑推理

构造证明法

附加前提证明法

归谬法（反证法）

题：命题逻辑推理

一阶逻辑推理

题：一阶逻辑推理

题：一阶逻辑推理

第 3 章 集合和矩阵

3.1 集合

空集 Ø

全集 E

幂集

相对补 绝对补 对称差

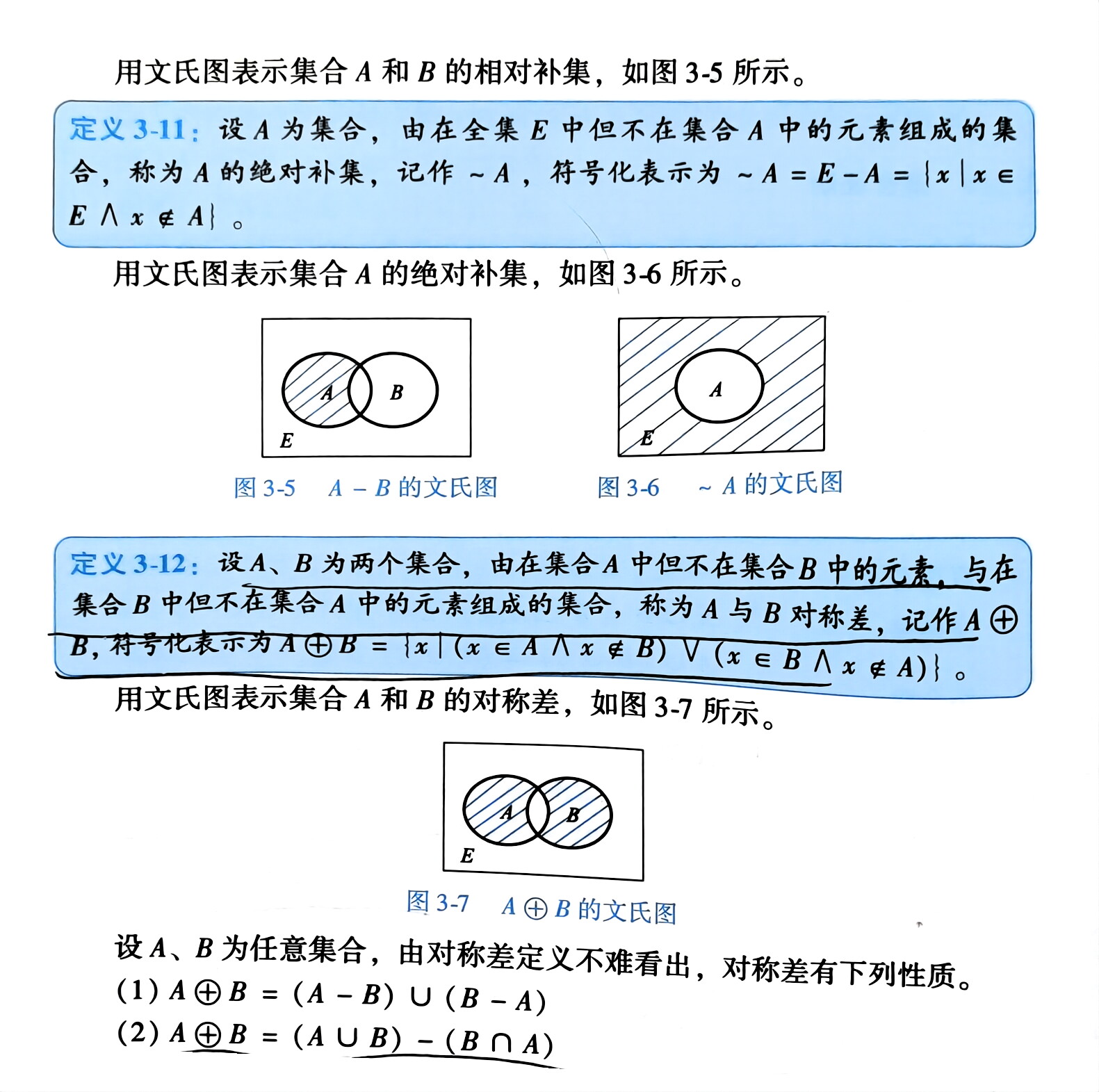
题：集合运算

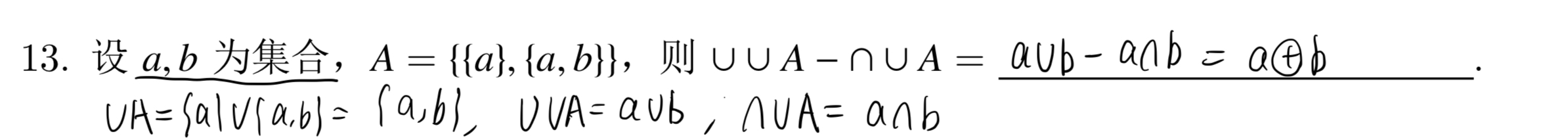
集合证明

命题演算法

等式代入法

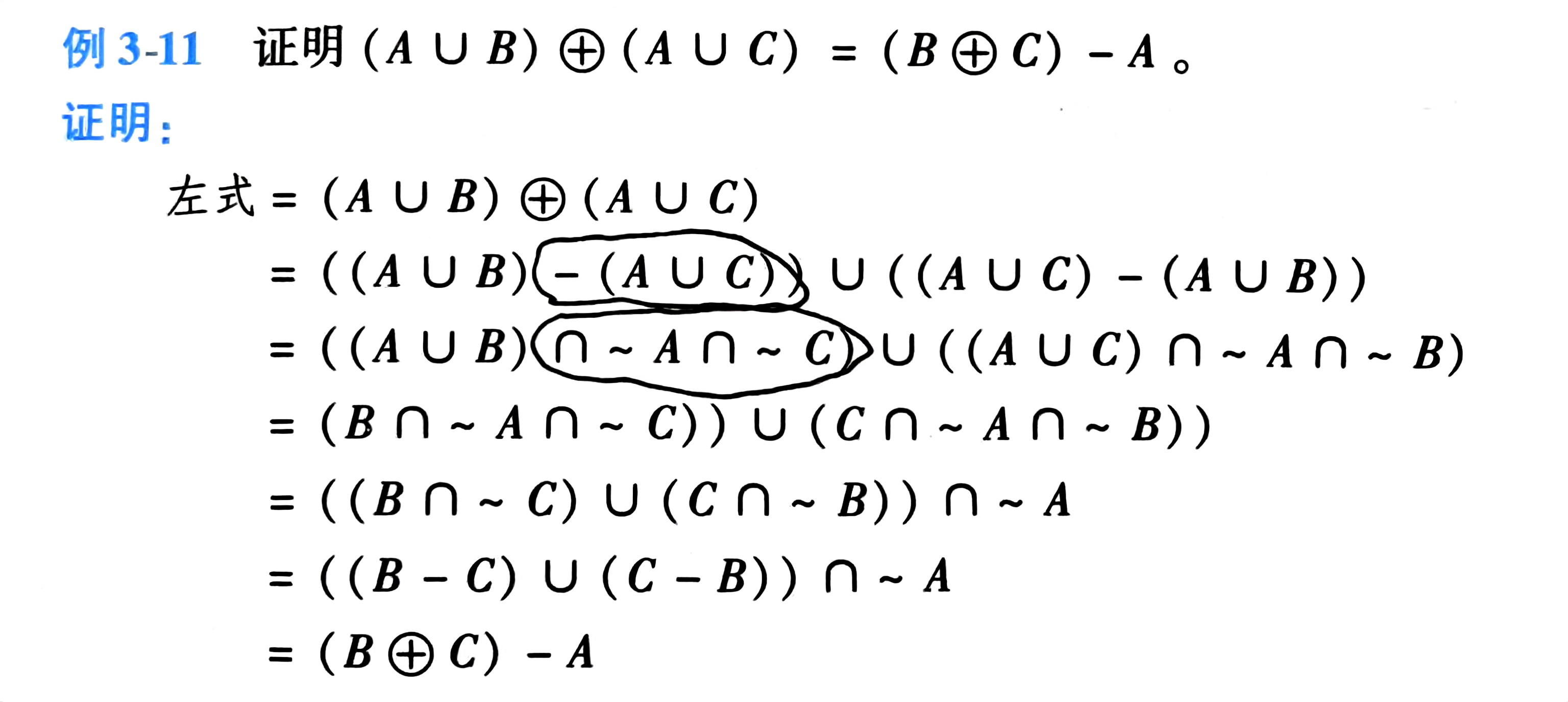
题：集合证明

3.2 矩阵

乘法 布尔矩阵

第 4 章 关系和函数

4.1 关系

有序对 元组

笛卡尔积

二元关系

全域关系 $E_A$

恒等关系 $I_A$

集合表示法

关系图表示法

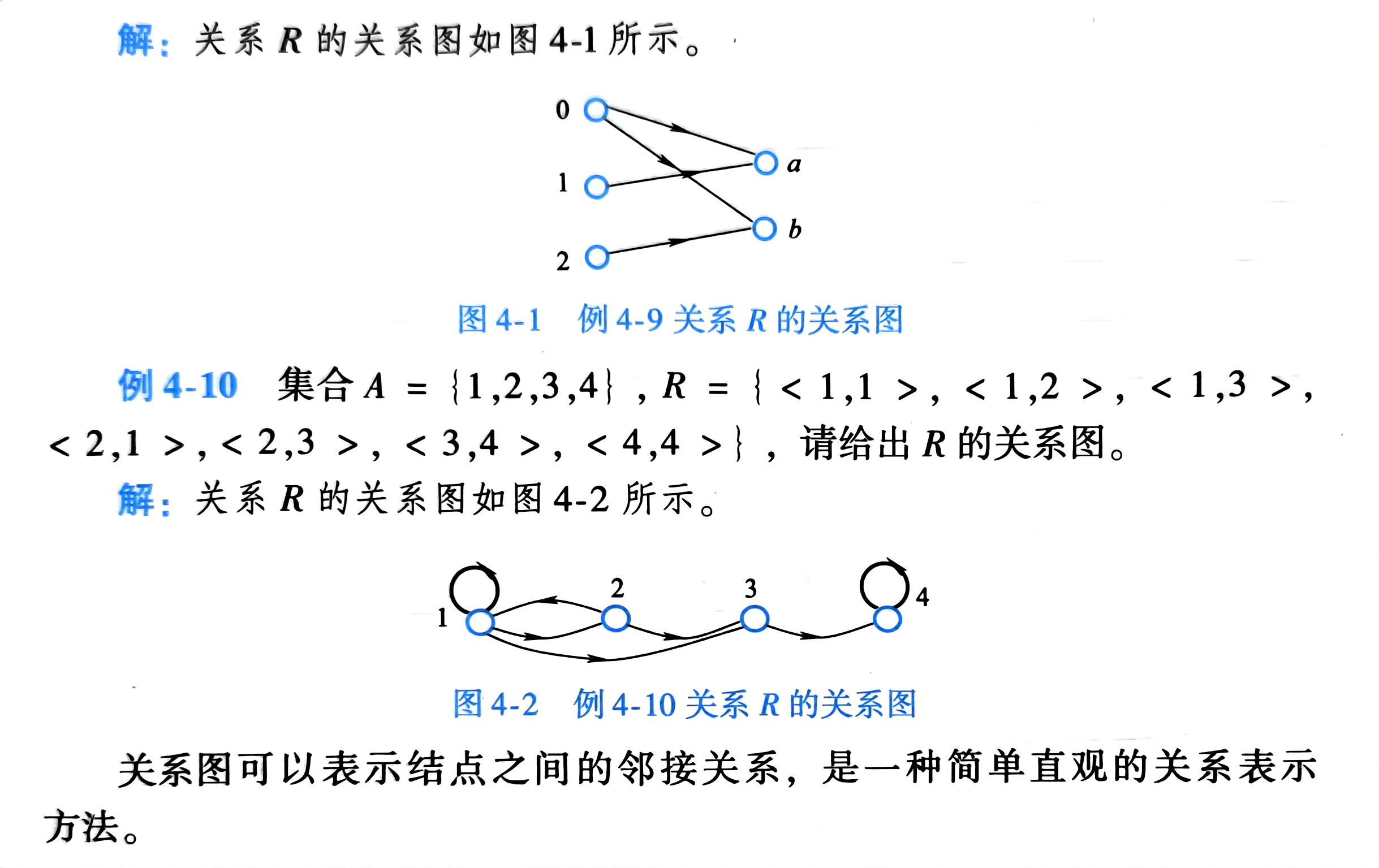
矩阵表示法

定义域 值域 域

关系的逆

复合关系

关系幂集

题：关系运算

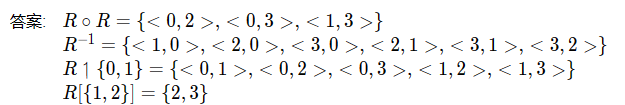
自反 对称 传递

反自反就是任何一个元素都不满足自反

不自反的关系不一定是反自反关系，反自反关系一定是不自反的关系

对称同理

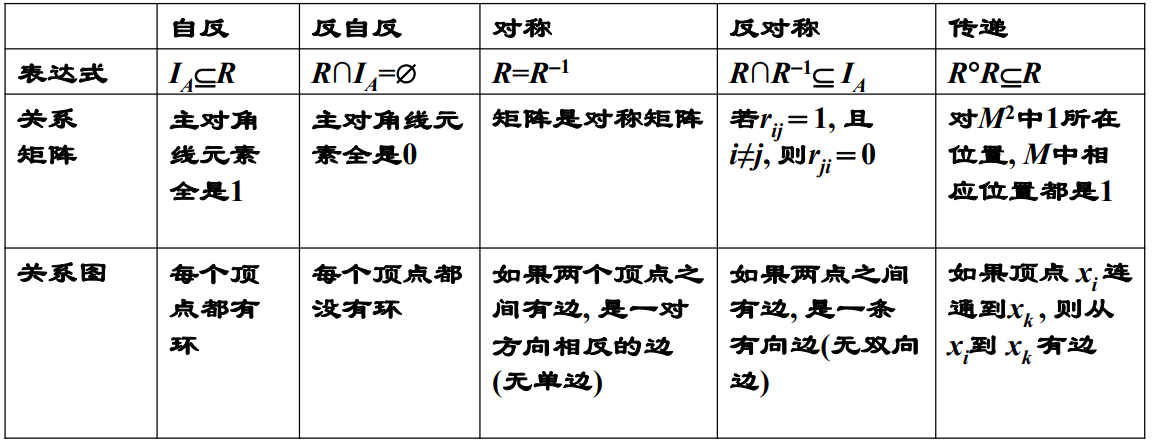
题：自反 对称 传递

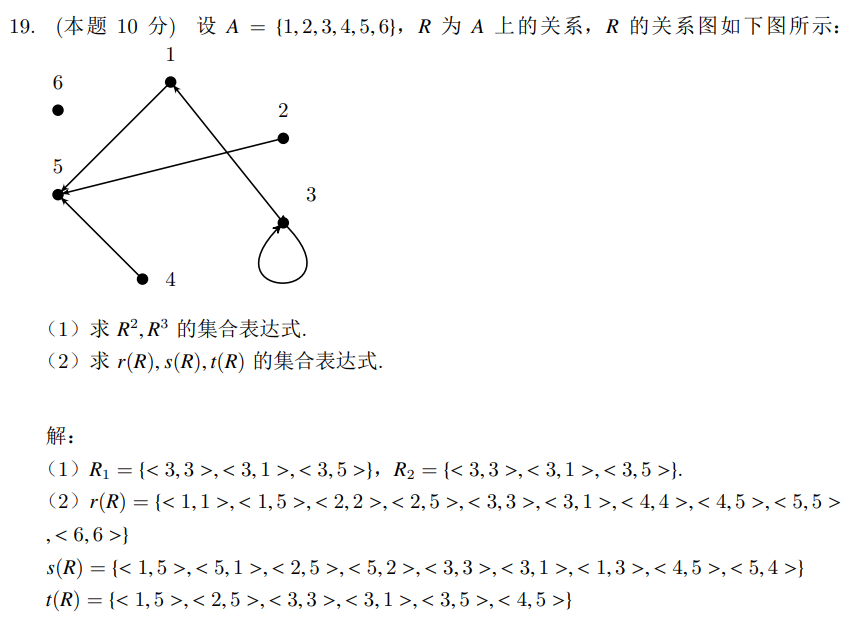
题：自反 对称 传递

关系闭包

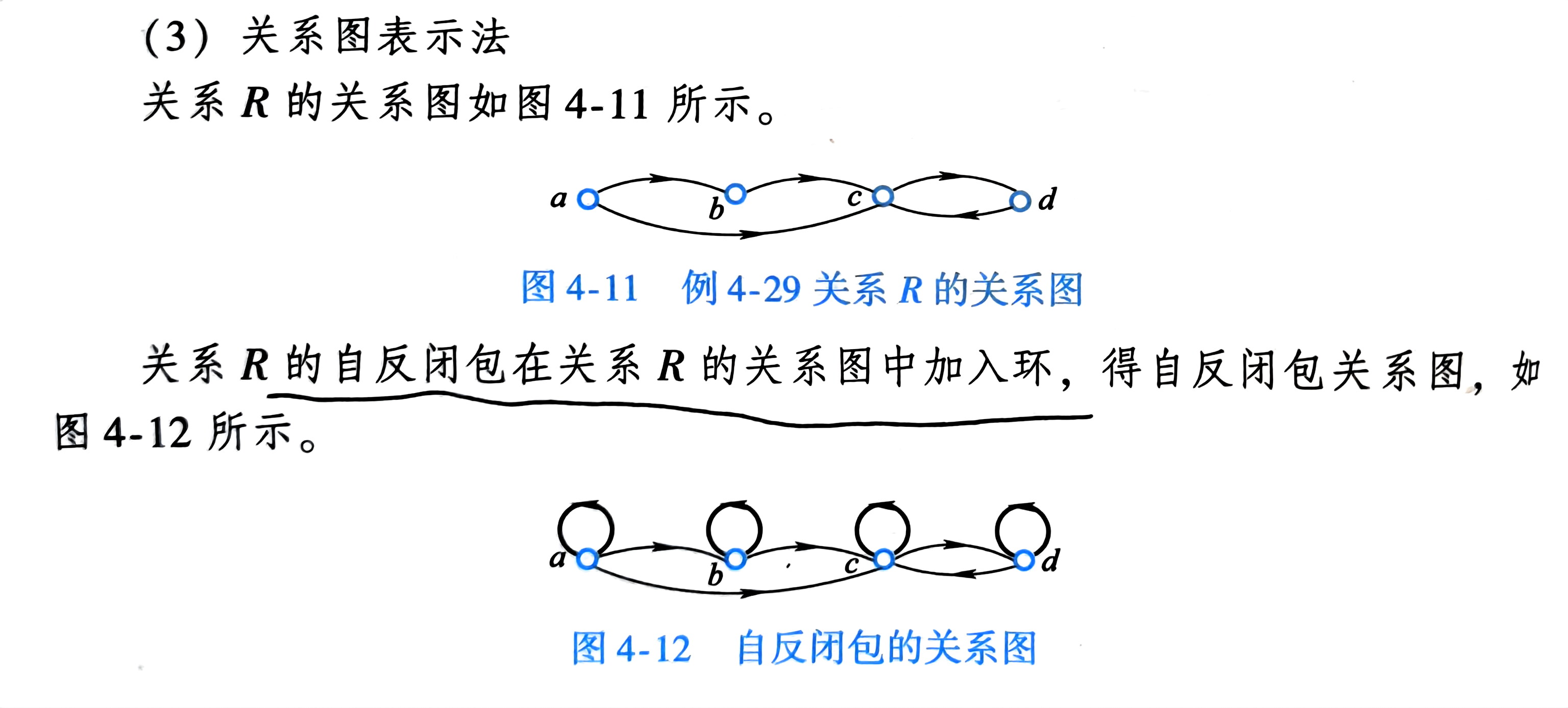
等价关系

等价类

商集 划分

等价类是集合，商集就是所有等价类构成的集合

题：商集

题：商集

偏序关系

哈斯图

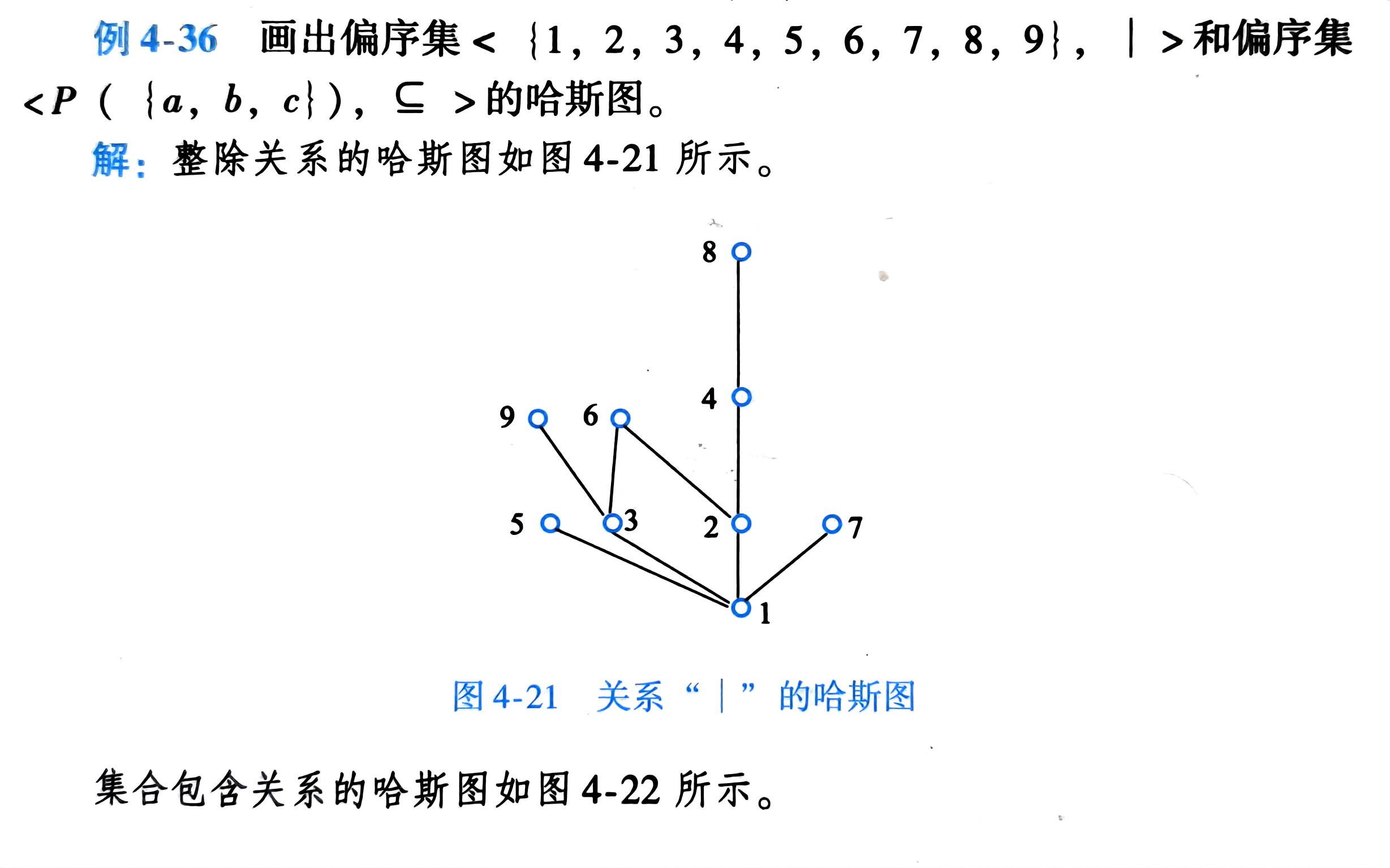
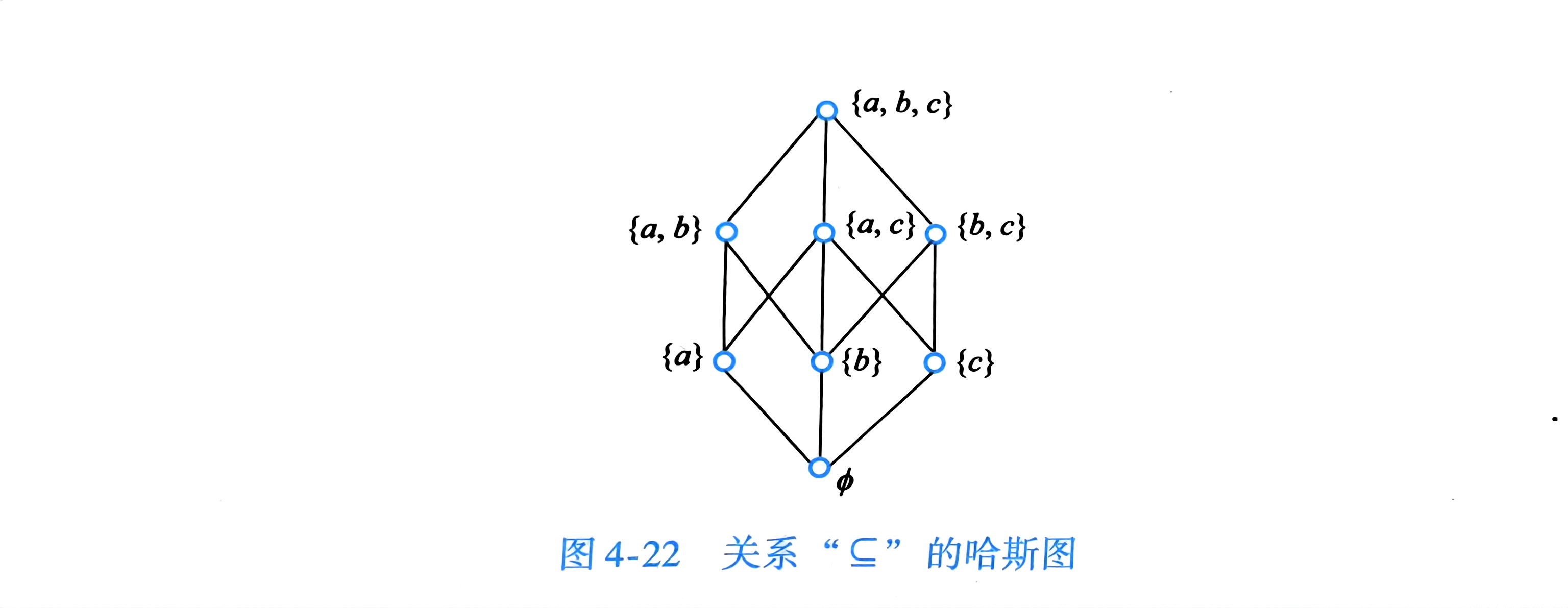
题：哈斯图

题：哈斯图

最小元 极小元 下界 下确界

4.2 函数

单射 满射 双射

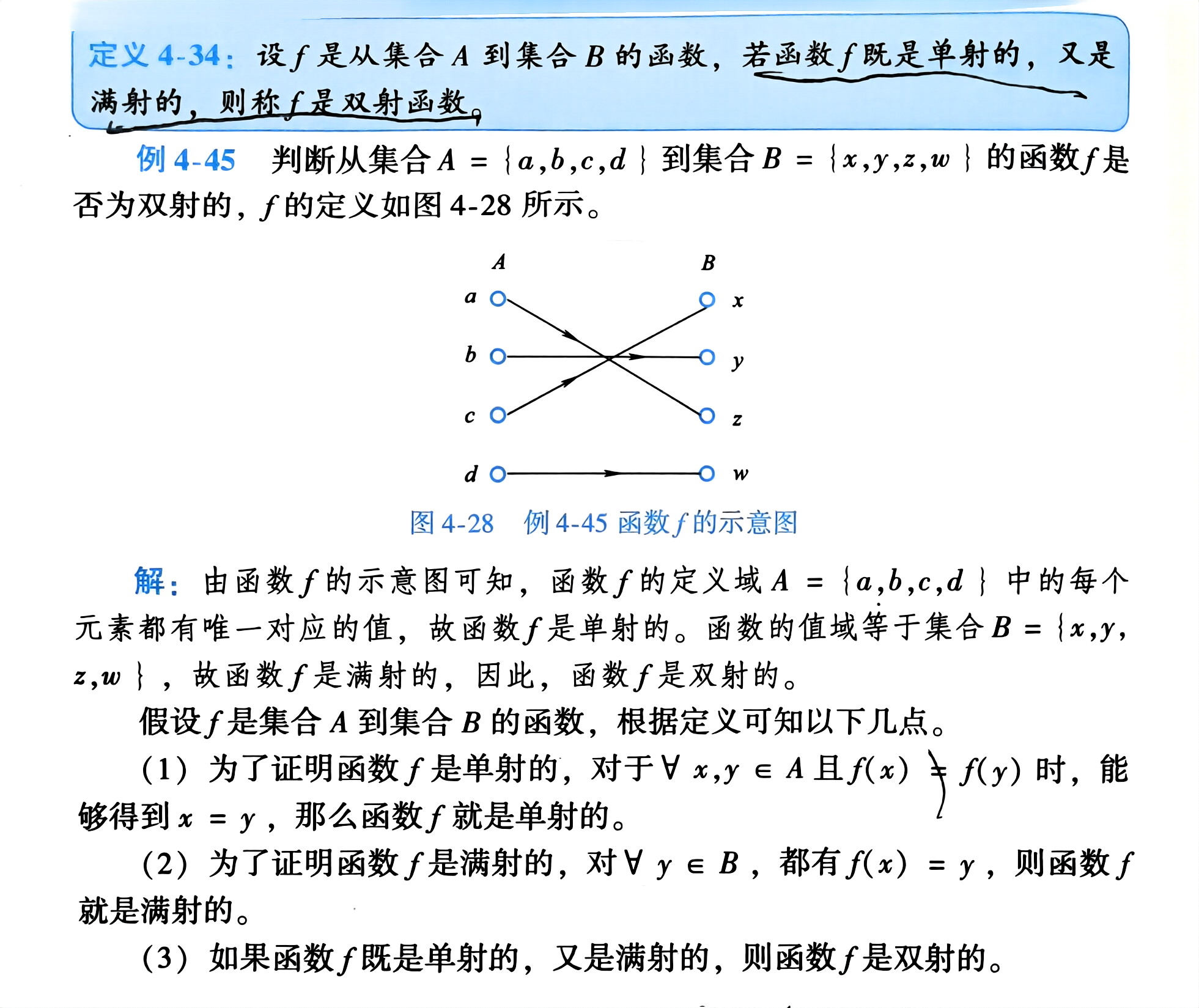
题：双射函数

逆函数

题：逆函数

复合函数

第 5 章 图的概念 矩阵表示

5.1 图的基本概念

顶点 阶 边 环 零图 平凡图

多重图 线图 简单图

5.2 度 度序列

度 度序列 正则图

5.3 握手定理

握手定理及其推论

5.4 完全图

完全图 补图

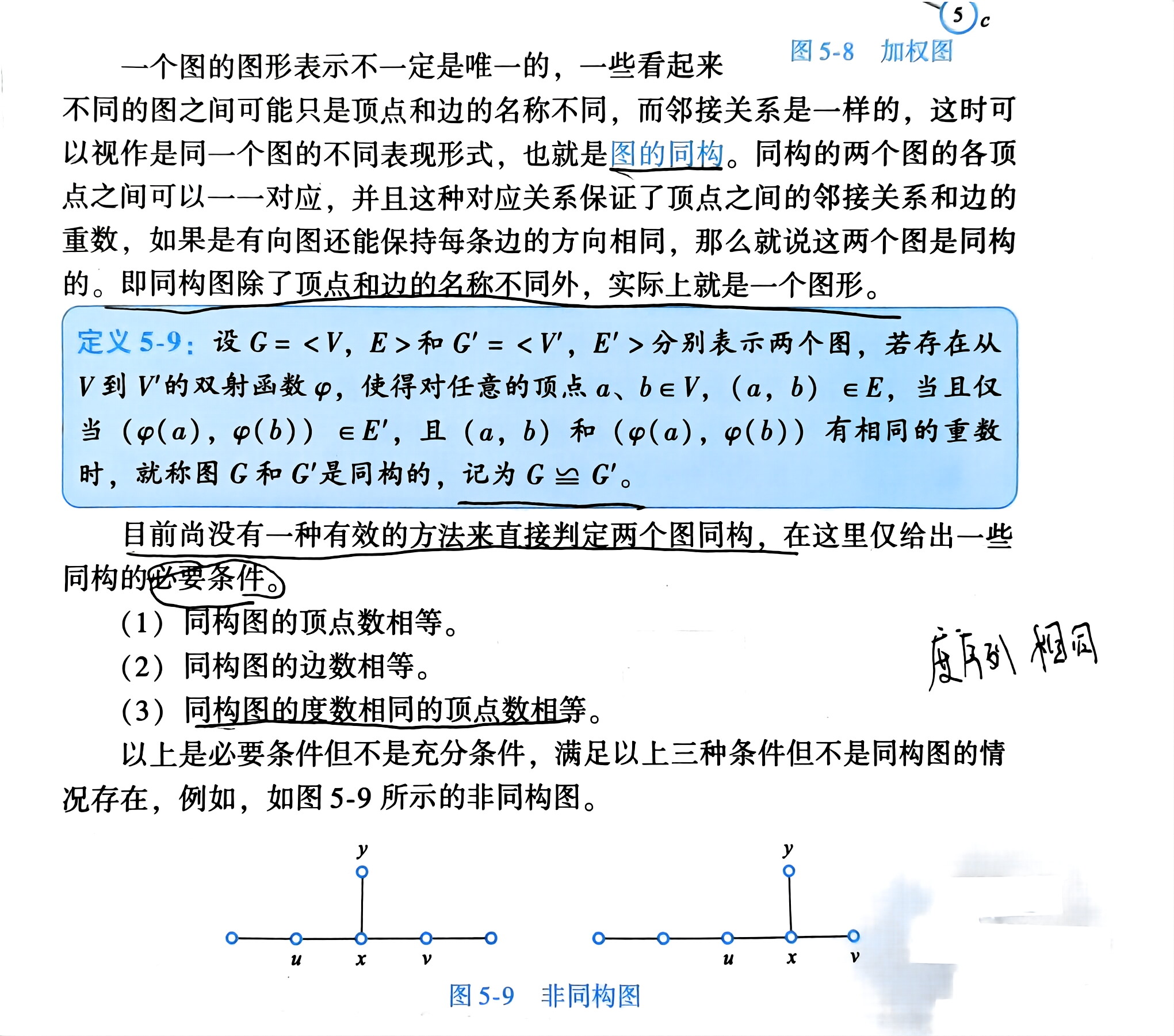
5.5 图的同构与子图

同构

子图 真子图 生成子图

5.7 通路 回路

通路 回路

简单通路：没有重复点

迹：没有重复边

通路 回路 计算

5.8 连通性

连通分支 割点 割边

连通度

弱连通 单连通 强连通

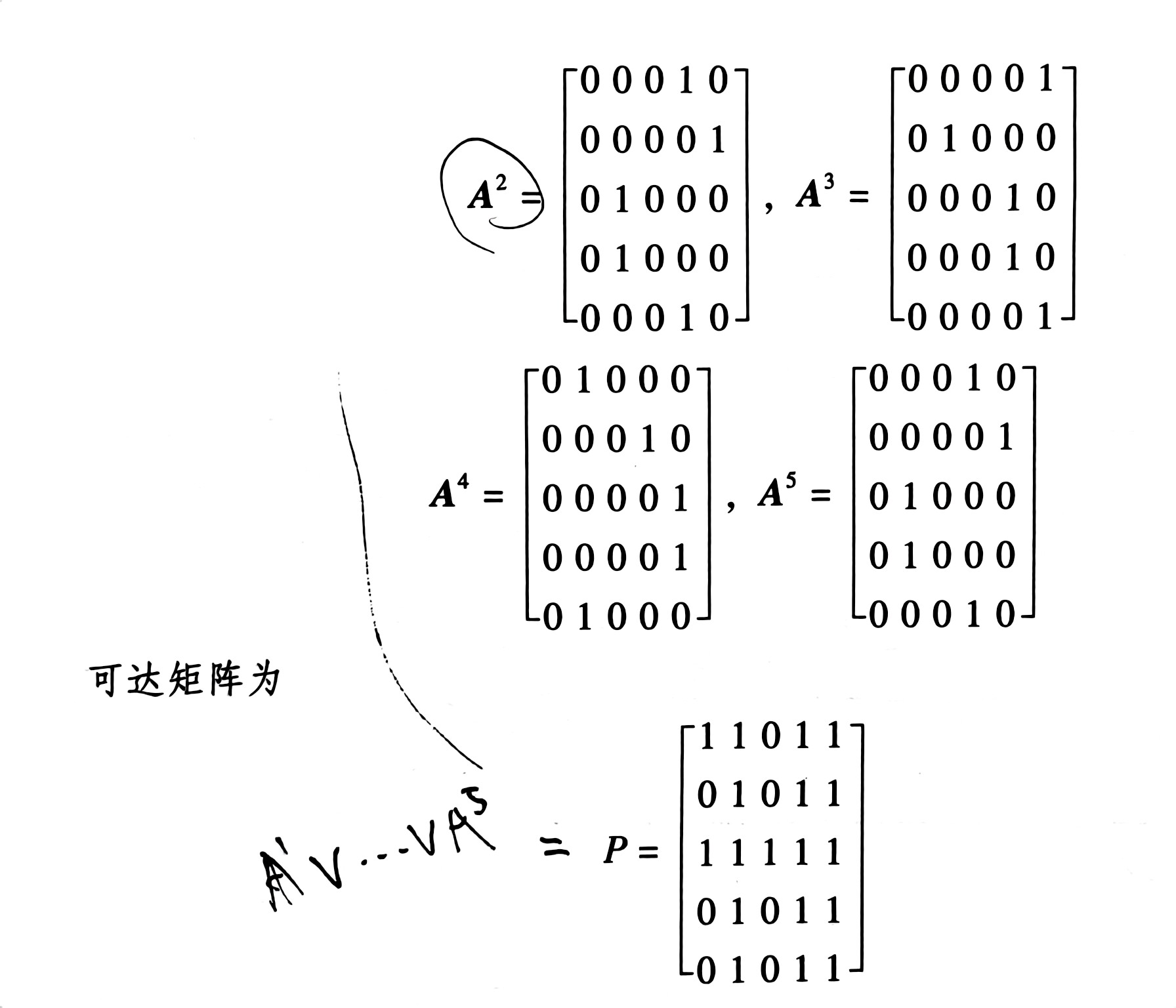
5.9 矩阵表示

邻接矩阵

可达矩阵

关联矩阵

连通性与矩阵

第 6 章 特殊的图

6.1 欧拉图

欧拉图 定义 判定

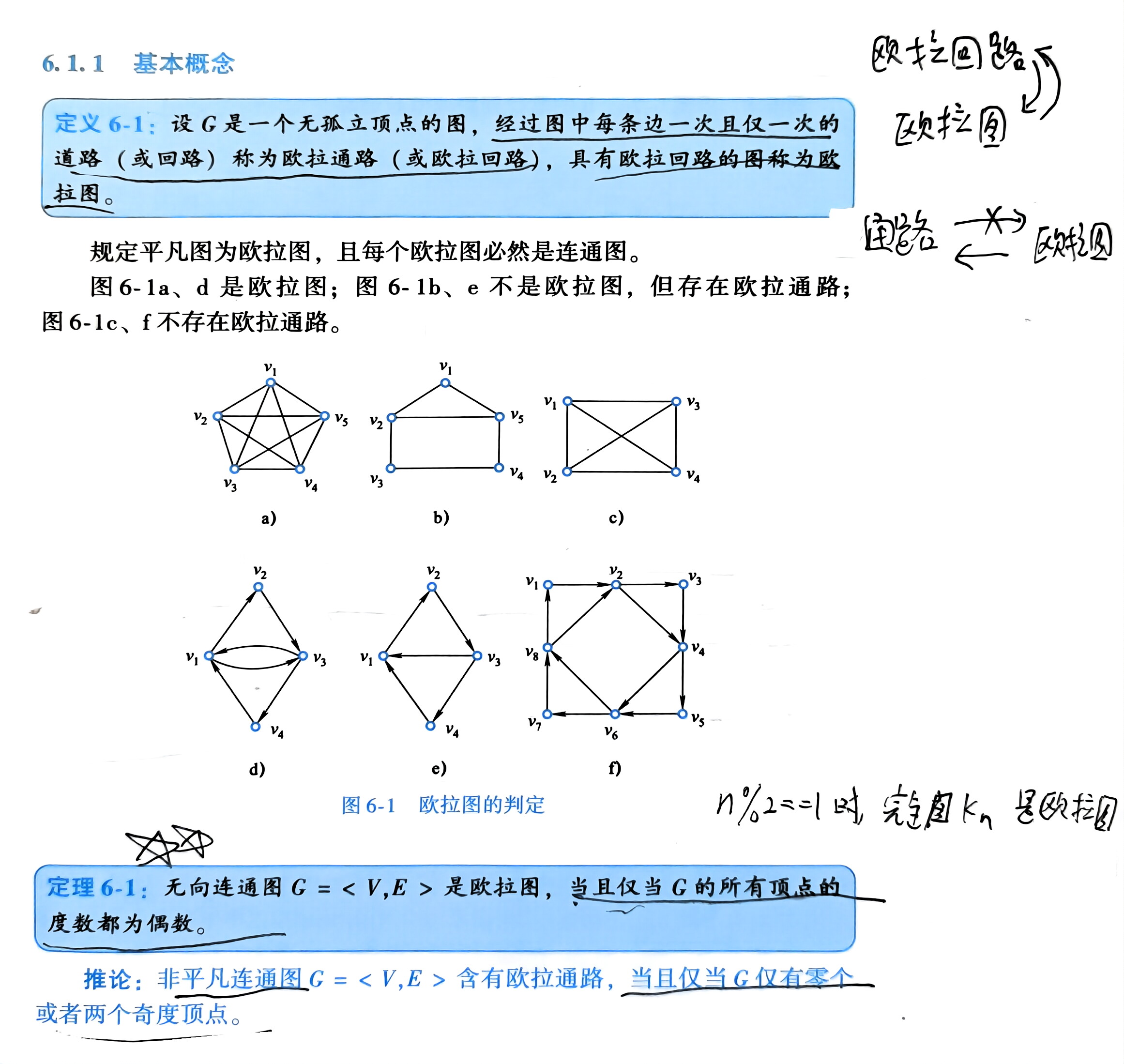
欧拉图 判定方法

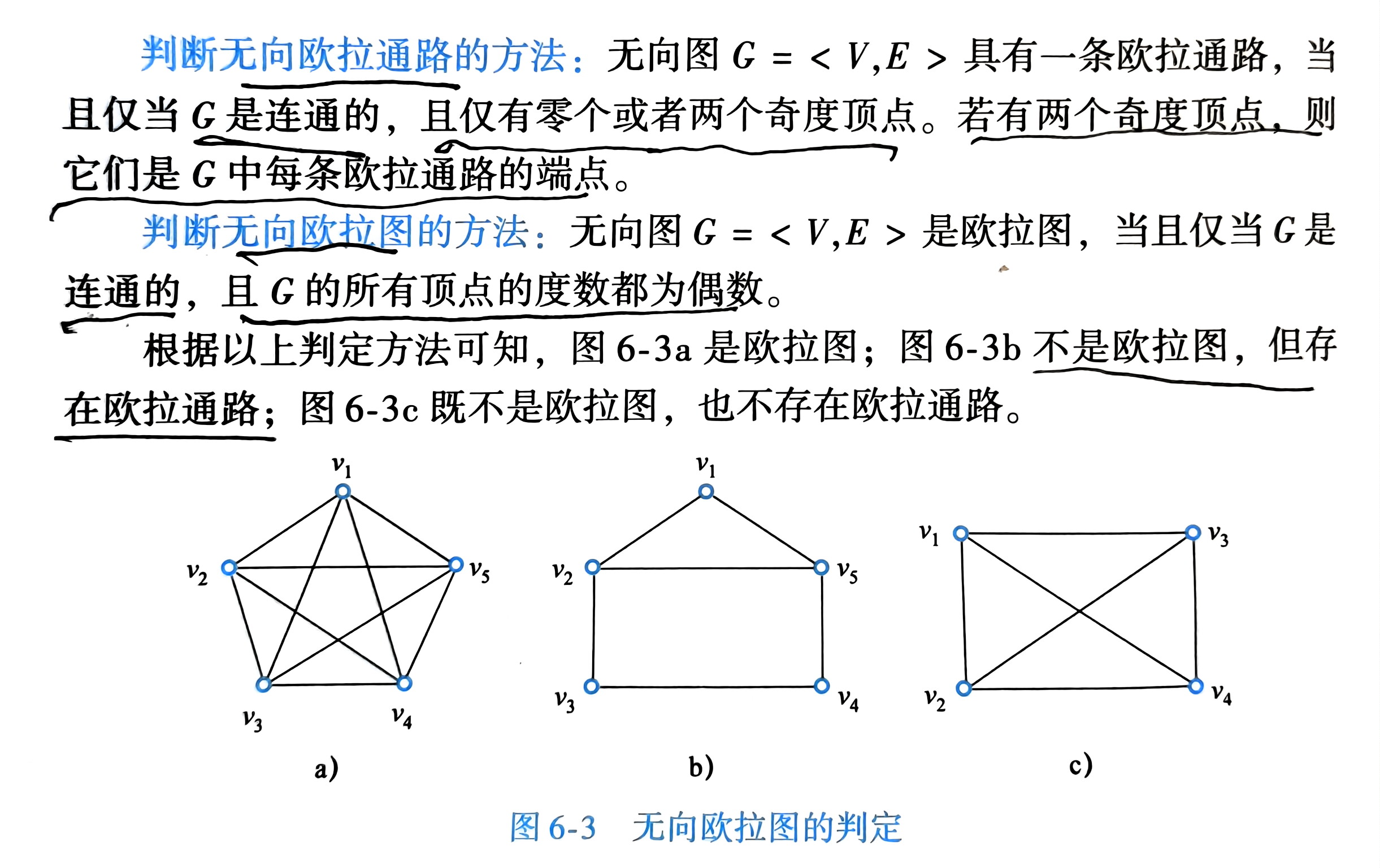
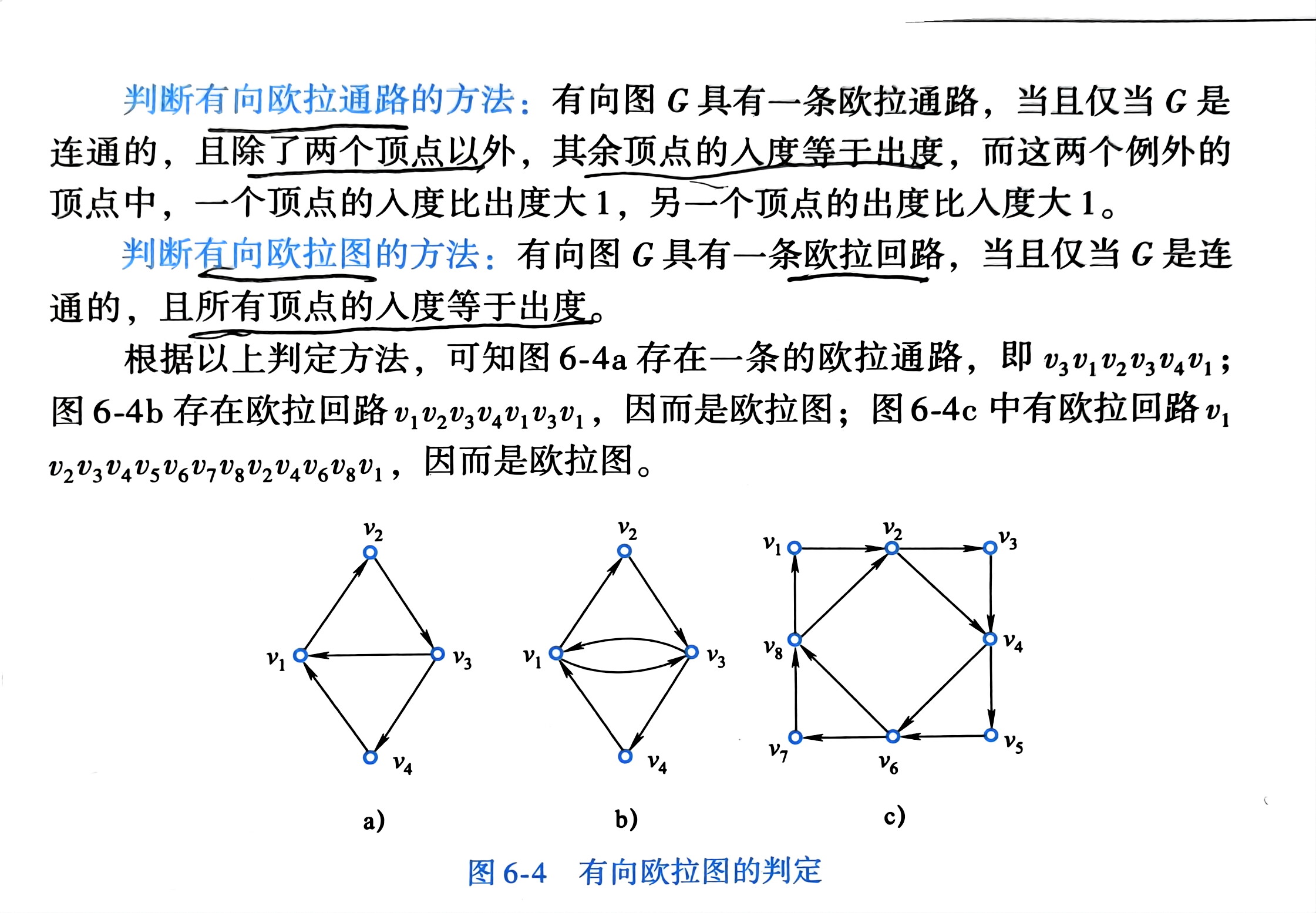
题：欧拉图

6.2 哈密顿图

哈密顿图 定义 判定

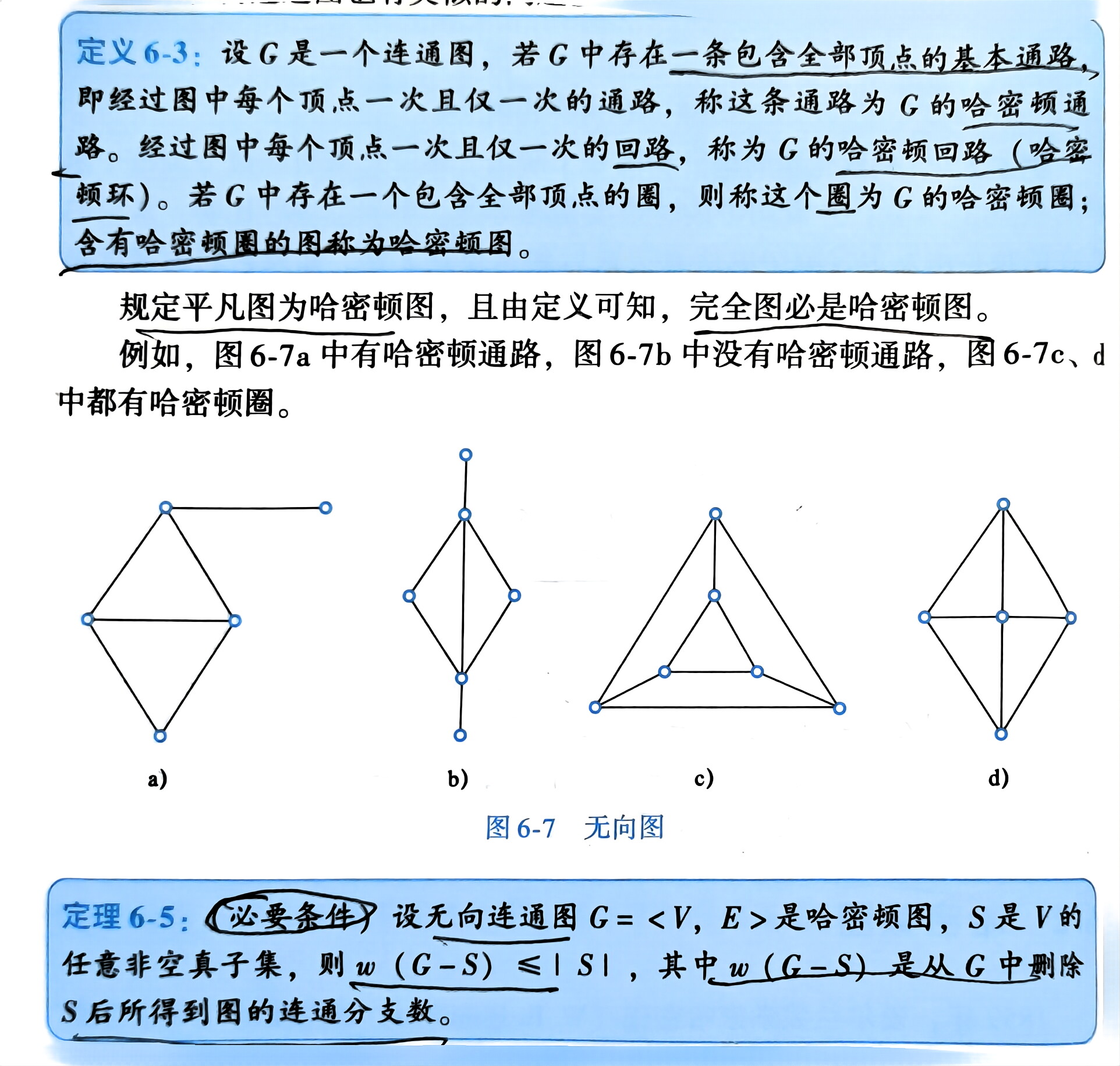
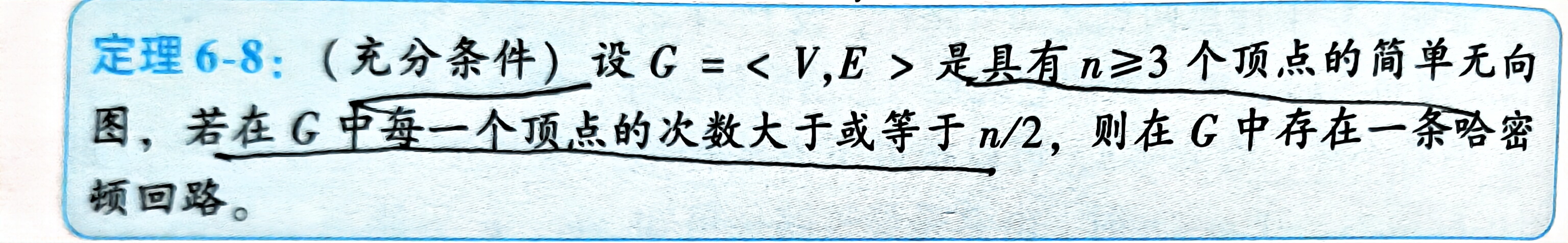
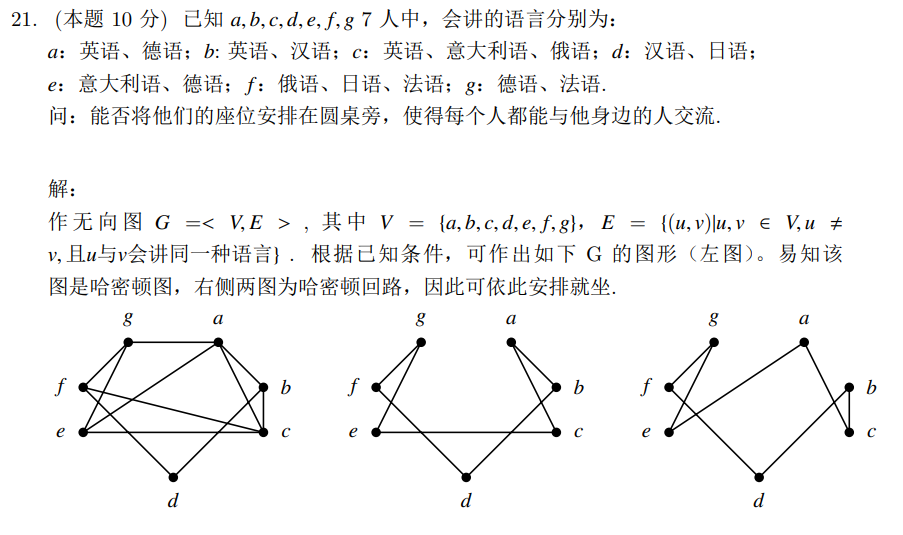
题：哈密顿图

6.3 二部图

二部图 定义 判定

二部图 = 偶图 = 二分图

匹配

霍尔定理

6.4 平面图

平面图 定义 性质

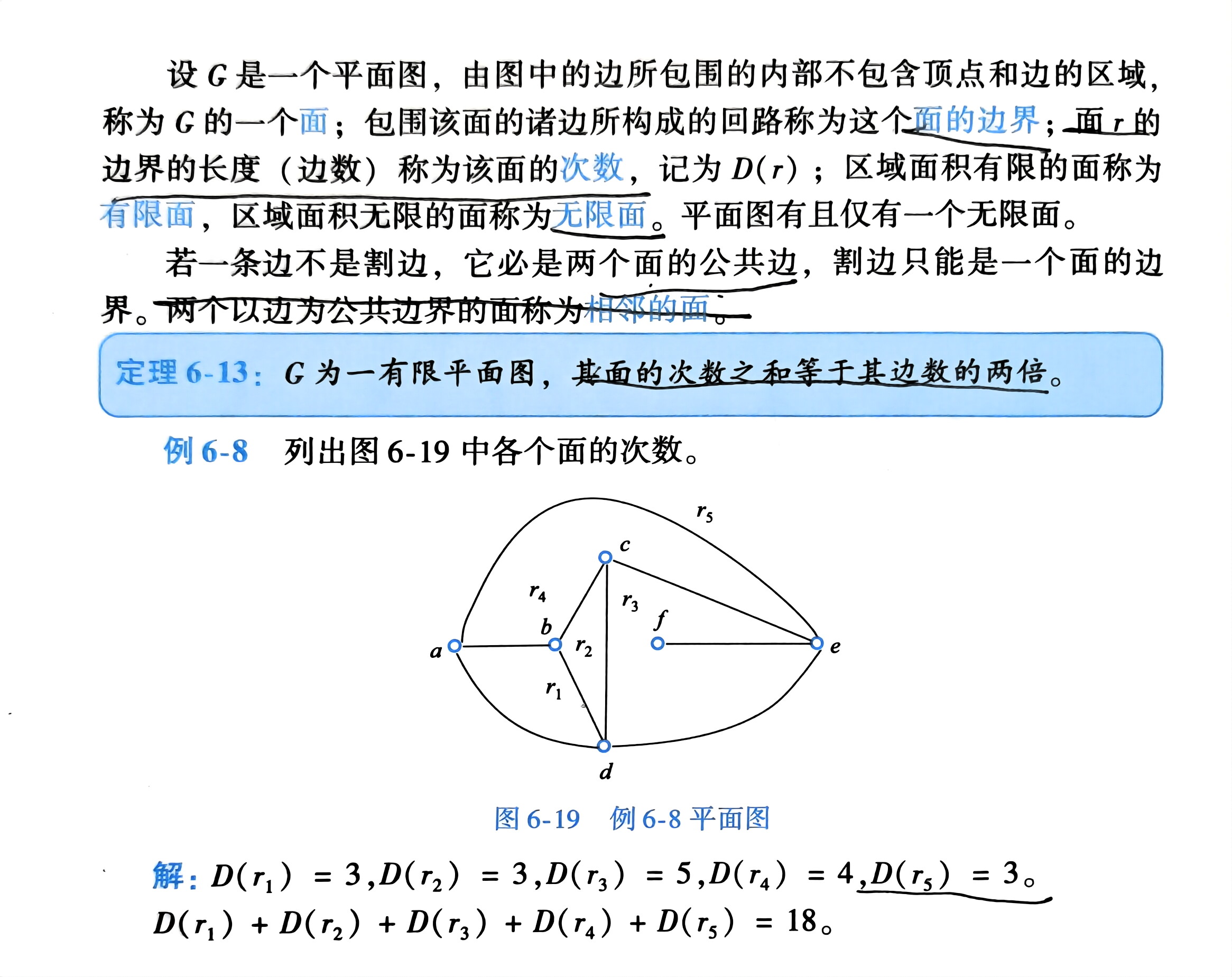
欧拉公式

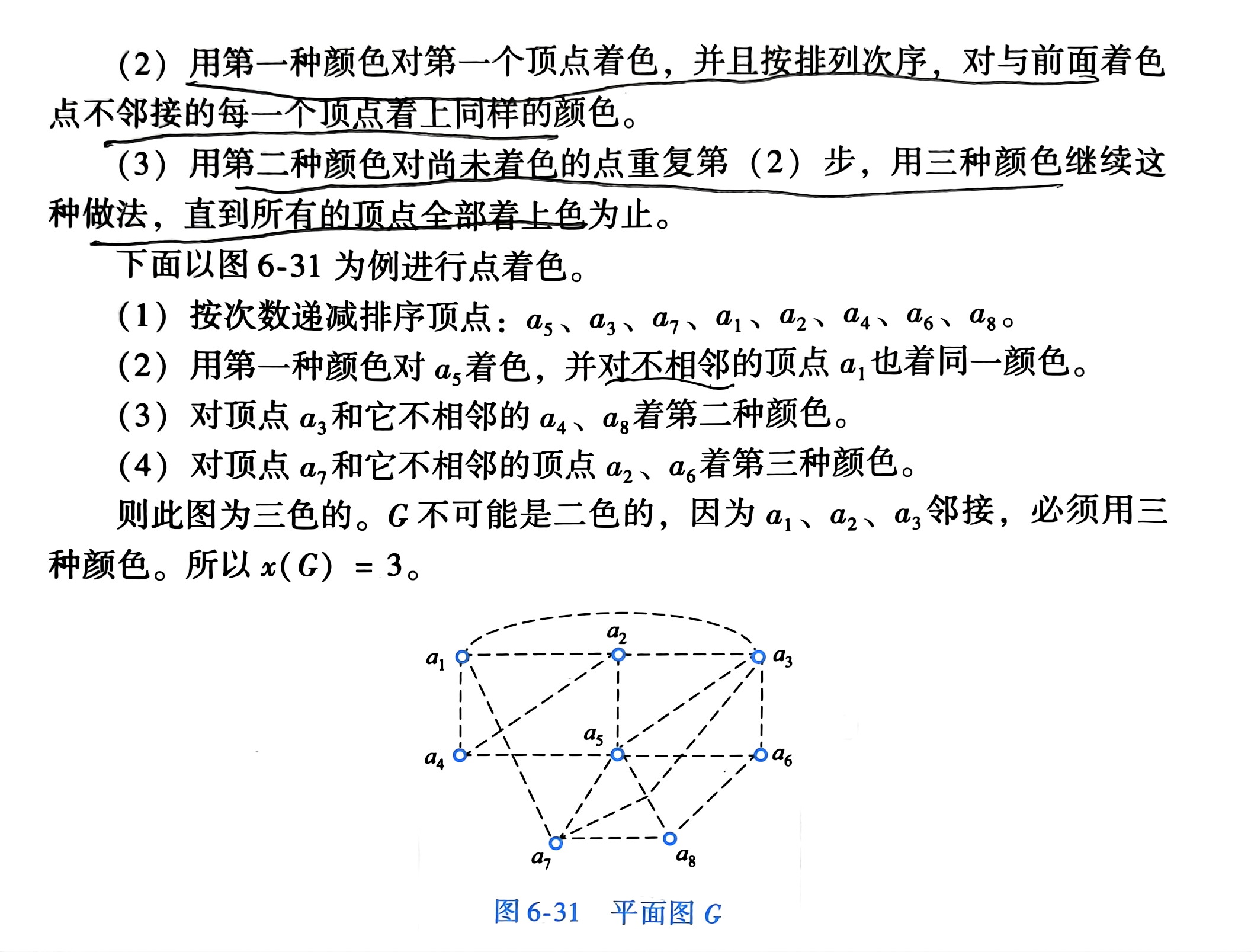
6.5 图的着色

对偶图

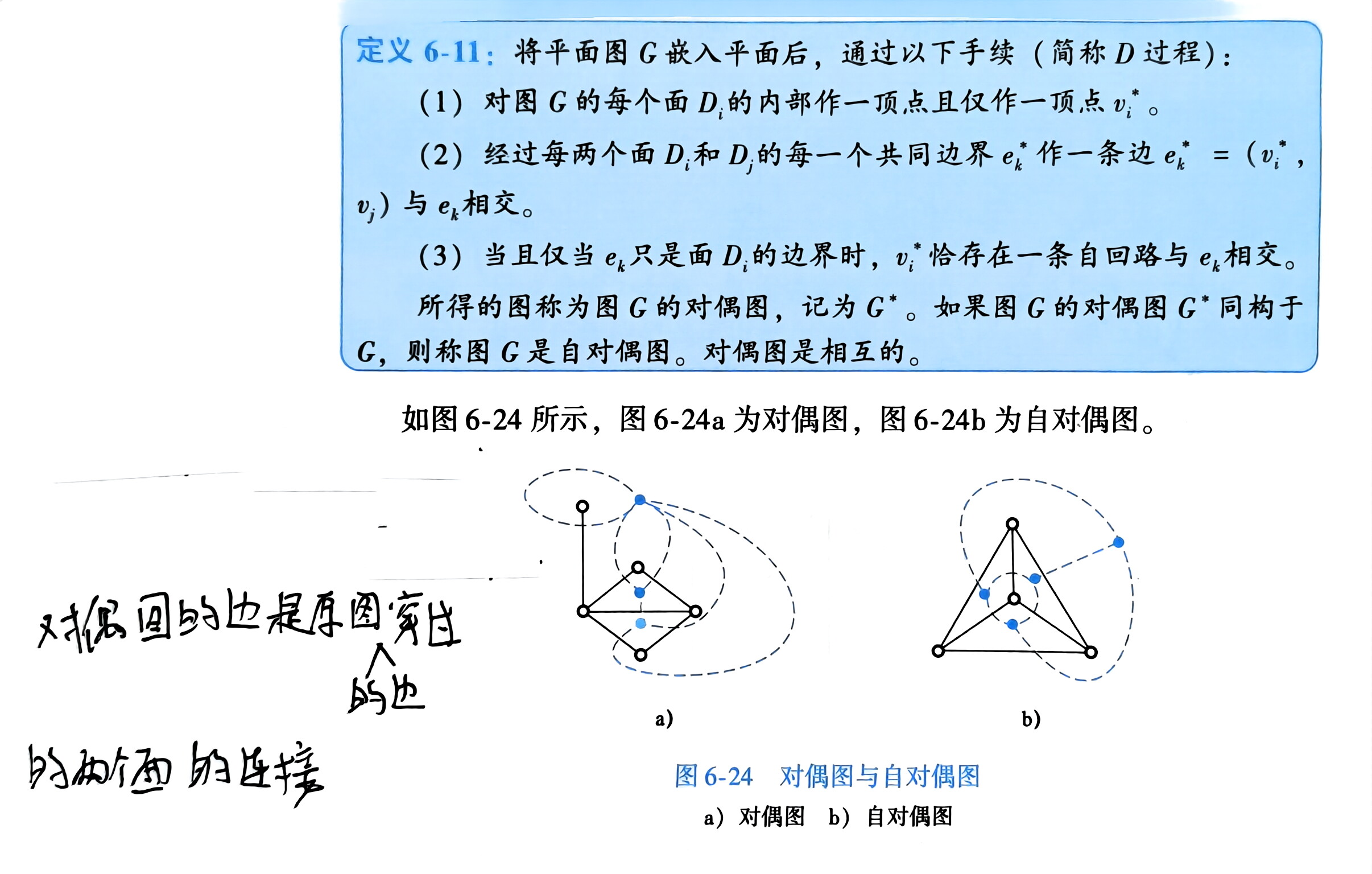
面着色

点着色