一题目

原题传送门：力扣
题目：

题目的意思是让你写一个数据结构，这个结构的特点和队列一样先进先出，然后完成：判断是否为空，判断是否为满，添加一个元素，删除一个元素，获取队尾元素，获取队首元素这些函数。
他和普通队列的区别是，这个循环队列它的空间大小是确定的，你给的值是k,这个队列就会给你开辟好k个元素大小的空间，满了就不能继续添加了。而队列是空间不够了可以继续开辟。

这个循环队列在满了之后，只有删除掉一个元素才能继续添加新的元素。

二.思路

2.1链表

接触过队列的应该都知道，队列是先进先出，用链表来实现比较容易，那我们这个循环队列可不可以用链表来实现呢？现在先分析一下链表实现可不可以，如果可以的话，再看容不容易实现。首先可以判断的是要实现一个循环队列，我们可以用循环链表实现：

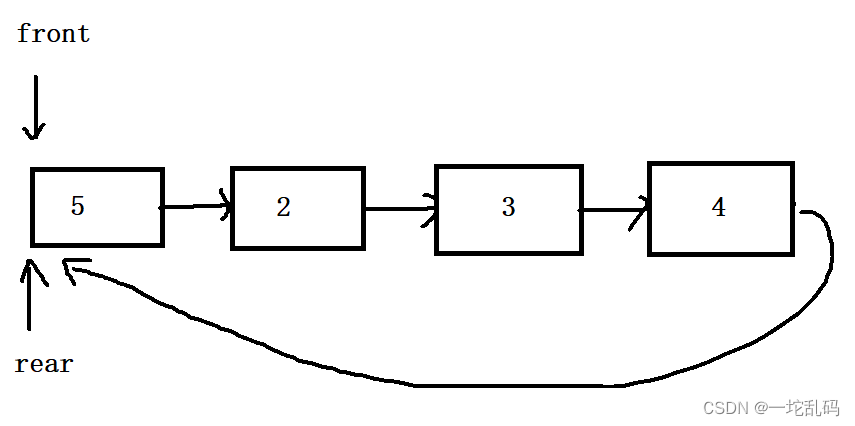
假设开辟了四个元素的空间，也就是这个队列最大能放四个元素。然后定义两个指针方便我们找到头和尾，每添加一个元素rear往后走一步，front不变。每删除一个元素front向后走一步，rear不变。这里可以看到判断是否为空这个函数很好写：看看两个指针指向的位置是否相等就行。但是判满呢？rear一直向后走走到最后的时候又回来了。
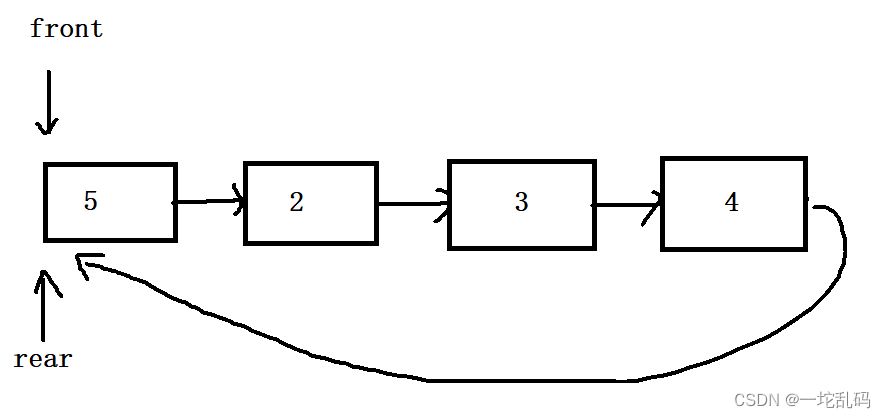现在我们发现front和rear相等的时候可以判断是满，这样子就和判空的函数判断条件冲突了。所以在这里我们有改进了一下。多开辟一块空间：

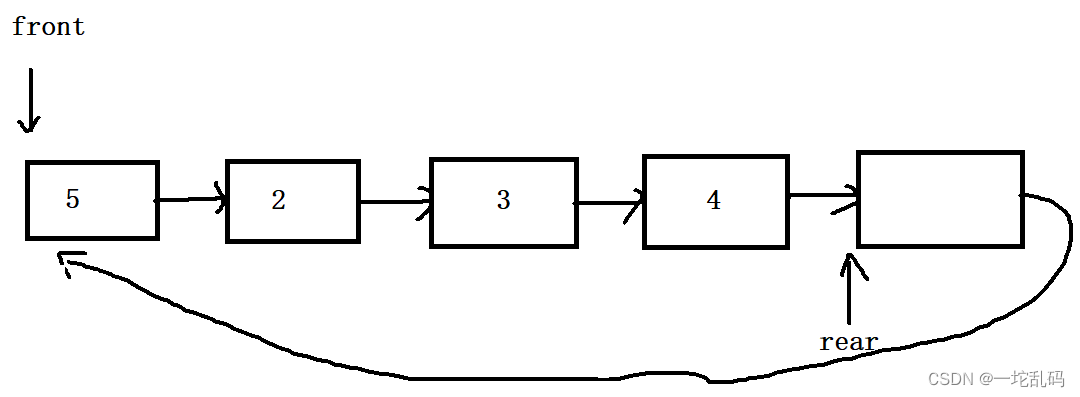
此时还是只能放4个元素，多出来的那一块只是为了方便判断这样判满的条件就是rear->next是否和front相等。

现在可以看到判空判满是挺好写的，再仔细观察，尾插就是需要加入的元素放在rear指向的节点里，首删就是让front向后走一步就行。这样的话尾插首删这两个函数也很容易写出来。

再来看最后两个函数获取队列首元素和尾元素，首元素是把front指向的元素返回出来，这里最麻烦的是获取尾元素，要获取尾元素，首先肯定要知道rear上一个节点的位置，但是我们这是单链表，上一个节点的地址需要在定义一个指针每次都指向rear指向这个节点的上一个节点，这样也能做出来，但是感觉不是那么方便。当然用双向循环链表也能实现，这样的话在开始开辟空间的时候也会比较麻烦。所以现在我想用另一种结构来实现这个循环队列：数组。

2.2数组

根据刚才对链表的分析，这个数组也需要多开辟一块空间，这里我们定义两个变量，front和rear，注意这里我们就不定义指针了，这两个变量表示的是相应的数组下标，用两个变量来表示的优势是它们是一个整数可以做一些指针做不了的运算。这里front,rear变化的方式和链表一样，每删一个元素front向后走一步，每添加一个元素rear向后走一步。
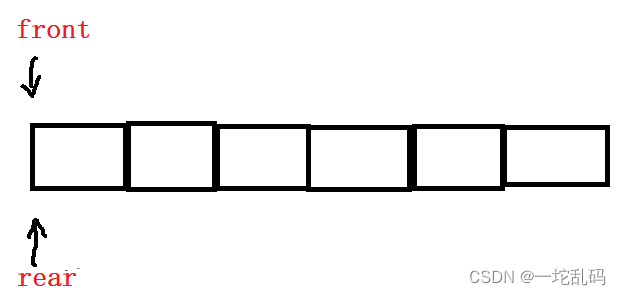这里假设开辟了5个元素大小的空间。判空很容易，看front和rear是否相等就行。
那判满呢？
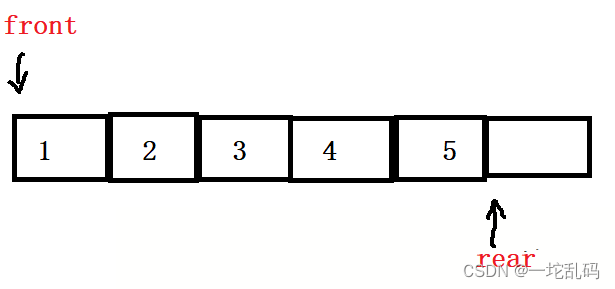是rear==5的时候就是满吗？如果此时删除两个元素：

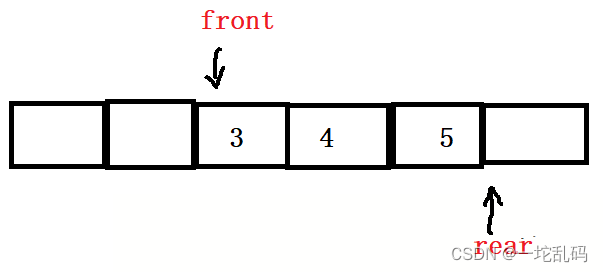现在我们再添加两个元素，这时候我们希望rear指向的地方是这里：
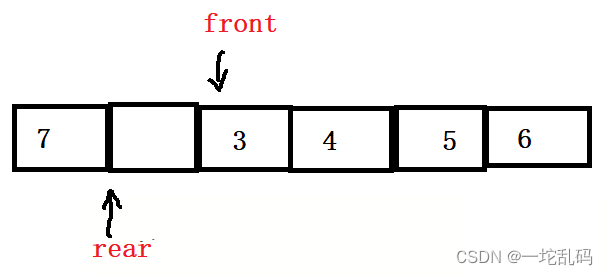这种情况rear的下一个位置如果和front相等就说明这个队列是满的。
所以队列满的情况有两种：
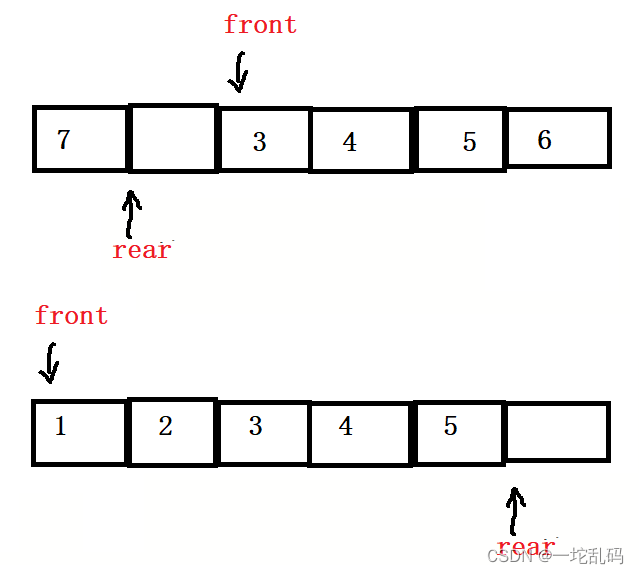虽然有两种情况但可以用一个式子来说明清楚：

判断(rear + 1) % (k + 1)的值和front是否相等
//这里的k就是队列最多的元素个数

这里的k我们设置的是5，看第一种情况，此时rear等于1，带进去这个式子结果是2%6 = 2，而2就是front的值，因为二者相等，所以可以说这个队列是满的。
再看第二种情况，6%6的结果是0，而且此时front也等于0，二者相等所以可以说这个队列是满的。

这样一分析这样写确实可以判断队列是不是满的。

现在开始想插入，删除的函数能不能写。
先看尾插：
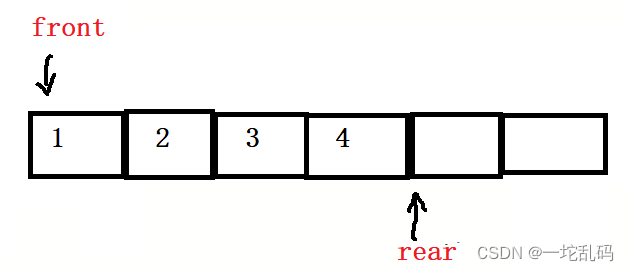这要在下标为rear的地方插入一个元素就行，看上去很容易，但是如果此时删除两个元素：
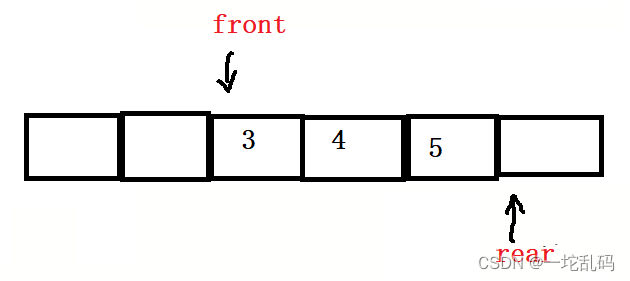在添加一个元素：
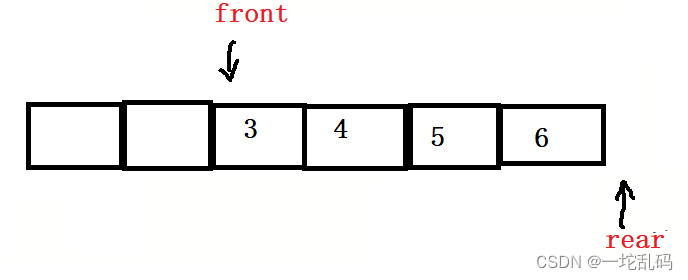如果再添加一个元素之前，我们希望rear代表的下标应该是这里：
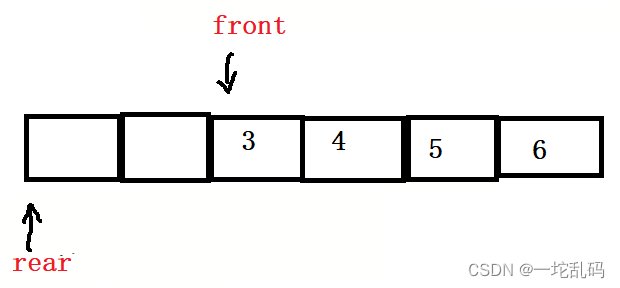也就是说rear在等于5的时候，然后在添加一个函数之前rear不等于6而是0，换句话说在添加一个元素后首先rear要往后走一步，而且做一步之后它所在的范围是0-5.所以我们可以这样写：

obj->a[obj->rear++] = value;
obj->rear %= (obj->k + 1);

同样在删除元素是front移动的规律和rear是一样的。

现在在考虑获取队首和队尾位置，获取队首的位置是最容易的，直接返回front所在下标的元素。
获取队尾稍微麻烦一点，因为我们要找的rear上一个的位置，其实麻烦也没麻烦多少，这里就需要多考虑一个特殊情况：
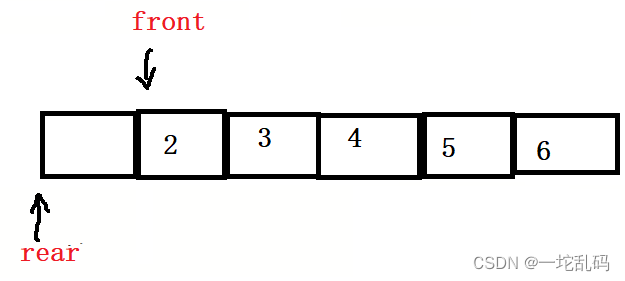当rear的值为0时上一个位置是-1，直接写的话会导致越界访问，而现在我们希望拿到的是a[k]也就是最后一个元素的位置。rear的取值范围是0-5，而我们希望得到的结果是1-5：
当rear为1-5的时候可以不用考虑，通过上面这图，就可以总结出一个规律：

(obj->rear + obj->k) % (obj->k + 1)

这样就把rear和需要的结果联系起来了，因为取模的是k+1，这样把结果规定在0-5这个范围内，而rear=0时需要的结果是5,所以在%前面加上一个k.

这样我们基本就把题目所需的函数都写出来了。最后释放函数把定义的几个指针free掉就行

三.代码

//定义一个指针a用来接收开辟的数组空间的地址
//front,rear代表数组下标，一个指向数组头，一个指向尾
typedef struct {
    int* a;
    int front;
    int rear;
    int k;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    obj->front = obj->rear = 0;
    obj->k = k;

    return obj;
}

//判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    assert(obj);
    //只有两个指针相等的时候才算空
    return obj->rear == obj->front;
}

//判满
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    assert(obj);
    //rear的下一个和front相等
    //rear指向最后一个时是特例，此时rear的下一个应该等于0才算满
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

//尾插
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    assert(obj);

    //判满，空间是满的话不允许添加
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    //先将value的值放到此时数组下标是rear的地方，然后rear向后走一步
    obj->a[obj->rear++] = value;
    //rear的范围只能是0-5
    obj->rear %= (obj->k + 1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    assert(obj);

    //判空
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front++;
    obj->front %= (obj->k + 1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    assert(obj);

    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }

    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    assert(obj);

    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }

    return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}