背景:
有人求助到博主希望分析一下他们老师给出的题目,博主思路分析和解题过程如下
题目要求:
联络矩阵法,当 n 较小时可以用手算,当然也可以用计算机计算。但当 n 很大时,需要计
算机的容量很大才行。为此要探求有效的计算机算法,这里介绍的一种是由输入节点到输出
节点找最小通路集的计算机算法。
设系统是由 n 个节点组成的有向网络系统,并设节点对间无并行弧,整个计算机算法的
思路为:
1 输入节点 I 作为起始节点;
2 由起始节点出发,选下一步可到达的节点 j;
3 判断节点 j 是否走过,若已走过则后退一步,以上一个节点作为起始节点,转②;
4 判断是否已达到输出节点 L,若未到,则把 j 作为起始点,转②;
5 判断是否已找到了所有的路,若否,则后退两步,把上面两个节点作为起始节点,
转②;
6 结束
由以上可见,计算机算法的关键是要进行几个判断:
1 判断节点是否与前面走过的节点重复;
2 判断是否已找到了一条路;
3 判断是否已找到了所有的路。
为了实现计算机算法,还需要定义如下:
1 可以描述从一个节点 j 可以进一步到达所有节点的矩阵,该矩阵称为路线矩阵,表
示为
[R(j,C(j))] R (1)
式中 j = 1,2,…,n
C(j)=1,
j
E 其中
j
E 表示 R 的第 j 行可到达的节点数。
路线矩阵 R 的第 j 行记录了节点 j 可以进一步到达的所有节点标号。R 不一定是长方阵,
对于不同的行,列数不一定相等,可用 0 补齐。





过程思路【重要】:
大家不要被概念绕混了!!
将问题简单化,我们针对题目中题目中的有向图2进行分析!

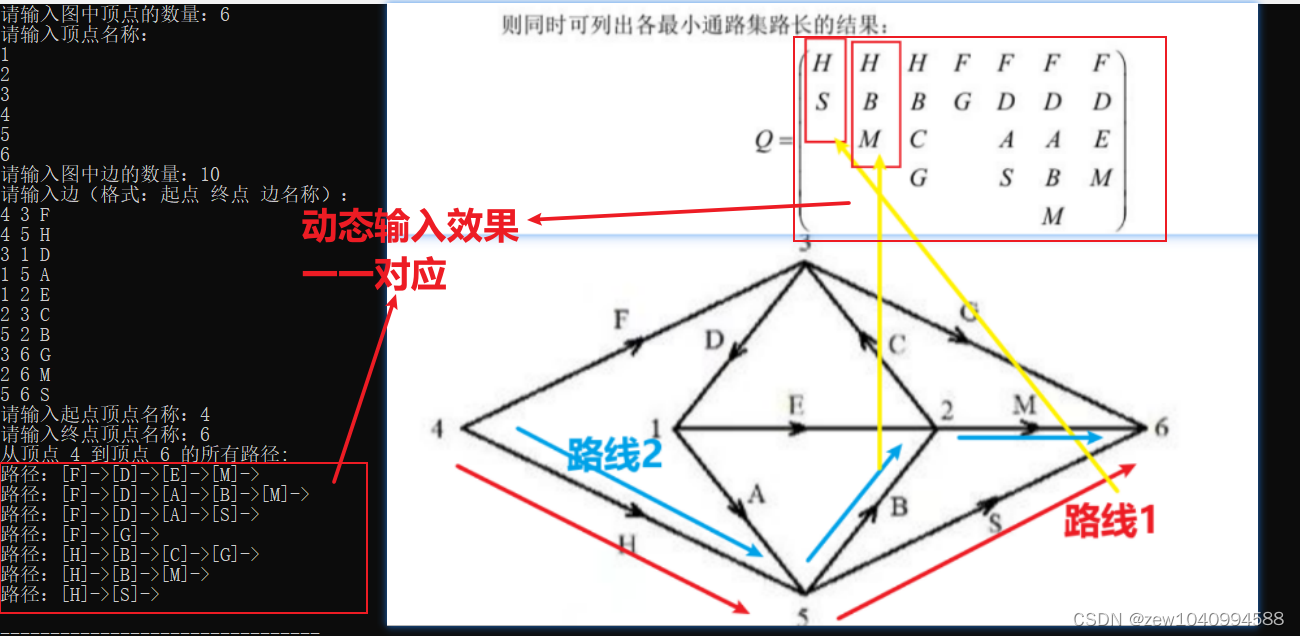
它其实就是一个求解起点4到起点6的一共有多少条路径的问题,给大家上一张图,大家应该就明白了!

可以看到H->S,H->B->M,H->B->C->D等一共7条线段,就是有向网络图2的,从起点4到终点6的所有最小通路集长的结果。
下面给出程序运行效果示例。
程序运行效果[用户可动态输入数据]:
程序可实现用户动态构造一个有向图,用户输入起点和终点,程序最终输出从该起点到终点的所有路径。
主要代码:
//联系请加V:zew1040994588
int main() {
DirectedGraph graph;
int numVertices, numEdges;
char vertexName[20];
char startVertexName[20], endVertexName[20], edgeName[20];
printf("请输入图中顶点的数量:");
scanf("%d", &numVertices);
initDirectedGraph(&graph, numVertices);
printf("请输入顶点名称:\n");
for (int i = 0; i < numVertices; i++) {
scanf("%s", graph.vertexNames[i]);
}
printf("请输入图中边的数量:");
scanf("%d", &numEdges);
printf("请输入边(格式:起点 终点 边名称):\n");
for (int i = 0; i < numEdges; i++) {
scanf("%s %s %s", startVertexName, endVertexName, edgeName);
addDirectedEdge(&graph, startVertexName, endVertexName, edgeName);
}
printf("请输入起点顶点名称:");
scanf("%s", startVertexName);
printf("请输入终点顶点名称:");
scanf("%s", endVertexName);
findPath(&graph, startVertexName, endVertexName);
return 0;
}