只打了半场。
A. Replace C or Swap AB
首先如果存在某个 \(i\),使得 \(Y_i\) 是 C 且 \(X_i\) 不是,那么显然是不合法的,可以直接判掉。
那么除去上述情况 \(Y\) 中为字符 C 的位置 \(X\) 也只能是 C。它们把字符串分成了若干段,可以把每一段分开单独考虑。
对于只含 A/B 的一段 \(Y\),我们可以根据个数得出 \(X\) 在这段中应该把多少 C 替换成 A,剩下的换成 B。
发现题意只能从 AB 换成 BA,等价于把某个 A 向后移一个位置。
那我们希望我们放置的 A 尽量靠前,使最后能成功匹配的概率最大。因此根据已知数量,贪心地把靠前的 C 都替换成 A。
判断当前 \(X\) 中是否每个对应的 A 所在位置都不大于它在 \(Y\) 中的目标位置即可。
Code
const int N=2e5+5;
int T,n;
char s[N],t[N];
vector<int> x,y;
bool solve()
{
n=read();
scanf("%s%s",s+1,t+1);
int lst=0,cnt=0;
s[n+1]=t[n+1]='C';
for(int i=1;i<=n+1;i++)
{
if(t[i]=='C')
{
if(s[i]!='C') return 0;
int cnta=0,cntb=0;
int sa=0,sb=0;
x.clear(),y.clear();
for(int j=lst+1;j<i;j++)
{
if(t[j]=='A') y.push_back(j);
if(t[j]=='A') cnta++; else cntb++;
if(s[j]=='A') sa++;
else if(s[j]=='B') sb++;
if(t[j]=='C'&&t[i]!='C') return 0;
}
if(sa>cnta||sb>cntb) return 0;
for(int j=lst+1;j<i;j++)
{
if(s[j]!='C')
{
if(s[j]=='A') x.push_back(j);
continue;
}
if(sa<cnta) sa++,x.push_back(j);
}
for(int j=0;j<x.size();j++) if(x[j]>y[j]) return 0;
lst=i;
}
}
return 1;
}
int main()
{
T=read();
while(T--)
{
int res=solve();
if(res) printf("Yes\n");
else printf("No\n");
}
return 0;
}B. Make Multiples
Solution 1
容易知道令 \(x\) 成为 \(y\) 的倍数,所需的最小操作次数为 \((y-(x\bmod y))\bmod y\)。
我们分别令 \(x=a,b,c,ab,bc,abc\),求每个数成为 \(x\) 的倍数所需的最小次数,并升序排序。那么当前 \(x\) 下只有操作次数最小的三个 \(a_i\) 可能被计入答案。
这样我们一共获得了至多 \(X=3\times 6=18\) 个 \(a_i\),暴力在它们之间 \(O(X^3)\) 枚举哪三个数成为 \(a,b,c\) 的倍数,统计最小值即可。
Solution 2
考虑状压。设 \(f_{i,j}\) 表示考虑了前 \(i\) 个数,已经存在倍数的数为集合 \(j(j\in[0,2^3))\)。
枚举当前数要修改成哪些数的倍数,那么有:
直接转移,令 \(M=3\),时间复杂度 \(O(n 2^{2M})\)。
Code
#define int long long
const int N=2e5+5;
int n,a[N],vis[N];
struct node{int id,x;} c[N];
int b[3],L[N];
vector<int> d;
il bool cmp(node x,node y) {return x.x<y.x;}
il int lcm(int a,int b) {return a*b/__gcd(a,b);}
signed main()
{
n=read();
for(int i=0;i<3;i++) b[i]=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int s=1;s<8;s++)
{
int lc=1;
for(int i=0;i<3;i++) if((s>>i)&1) lc=lcm(lc,b[i]);
for(int i=1;i<=n;i++) c[i].id=i,c[i].x=a[i]%lc?lc-a[i]%lc:0;
sort(c+1,c+n+1,cmp);
for(int i=1;i<=min(n,3ll);i++)
if(!vis[c[i].id]) vis[c[i].id]=1,d.push_back(a[c[i].id]);
}
int ans=3e18;
for(int i=0;i<d.size();i++)
{
for(int j=0;j<d.size();j++)
{
for(int k=0;k<d.size();k++)
{
int res=0;
for(int l=0;l<d.size();l++) L[l]=1;
L[i]=lcm(L[i],b[0]),L[j]=lcm(L[j],b[1]),L[k]=lcm(L[k],b[2]);
for(int l=0;l<d.size();l++) res+=d[l]%L[l]?L[l]-d[l]%L[l]:0;
ans=min(ans,res);
}
}
}
printf("%lld\n",ans);
return 0;
}C. LU / RD Marking
把少打的半场时间补上大概能过。
Description
给一个 \(n\) 行 \(m\) 列的网格,那么它的所有网格线上共有 \(n(m+1)\) 条竖边,\((n+1)m\) 条横边。
有如下两种操作:
- 选一个上面和左面的网格线都没被涂黑的格子,并涂黑这两条线;
- 选一个下面和右面的网格线都没被涂黑的格子,并涂黑这两条线。
求执行两种操作若干次(可以为 \(0\)),可能得到不同的涂黑边集数量。
\(T\le 2\times 10^5,\ n,m\le 10^6\)。
Solution
在网格线上考虑问题,发现操作一次只会对该折线左下 / 右上相邻的折线产生影响。也就是说,我们把网格线斜向拆成若干条连续的折线,它们之间贡献独立。借用一下官方题解的图:
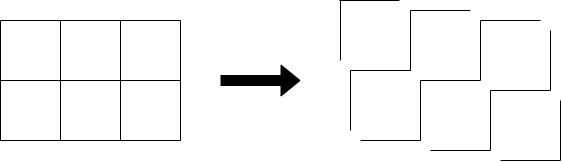
想到这一步就很好做了。
现在我们要求的就是对于每一条折线,在上面选若干长度为 \(2\) 的区间,且两两之间不能有交的方案数。
考虑 dp,设 \(f_n\) 表示长度为 \(n\) 的折线的答案。那么如果不选 \([n-1,n]\) 这条折线,\([n-2,n-1]\) 及以前的都可以选,方案数为 \(f_{n-1}\);否则只能选 \([n-3,n-2]\) 及以前的,方案数为 \(f_{n-2}\)。发现是斐波那契,预处理一下就好了。
统计一对 \((n,m)\) 的答案,这里设 \(n<m\),不满足就 \(\text{swap}\) 一下。
那么分成从横/竖边出发,把每条折线的贡献乘起来,则答案为
前面一半快速幂,后面一半预处理。
点击查看代码
#define int long long
const int N=2e6+5,mod=998244353;
int T,n,m;
int f[N],sum[N];
void init(int mx)
{
f[0]=1,f[1]=2;
for(int i=2;i<=mx;i++) f[i]=(f[i-1]+f[i-2])%mod;
sum[0]=1;
for(int i=1;i<=(mx>>1);i++) sum[i]=sum[i-1]*f[2*i-1]%mod*f[2*i-1]%mod;
}
il int qpow(int n,int k)
{
int res=1;
for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
return res;
}
signed main()
{
init(2e6);
T=read();
while(T--)
{
n=read(),m=read();
if(n>m) swap(n,m);
int res=sum[n];
res=res*qpow(f[2*n],m-n)%mod;
printf("%lld\n",res);
}
return 0;
}D. Interval Counts
这不比 C 简单。
Description
给定正整数 \(n\) 和长度为 \(n\) 的序列 \(x_i,y_i\),保证 \(x_i\) 单调递增。你要构造 \(m\) 个区间 \([L_i,R_i]\)(\(m\) 由你指定),使每个 \(x_i\) 恰好被 \(y_i\) 个区间包含。
求所有构造方案中 \(\min_{i=1}^m \{R_i-L_i\}\) 的最大值。
\(N\le 2\times 10^5,\ 1\le x_i,y_i\le 10^9\)。
Solution
看到最小值最大试图进行二分,然而不太可做。因此考虑直接贪心构造。
按 \(x_i\) 从小到大的顺序依次构造区间。
假设当前构造的区间已经满足 \(x_1,\dots,x_{i-1}\) 的限制。那么根据当前 \(y_i\) 和 \(y_{i-1}\) 的大小关系分为三种情况。
-
\(y_i=y_{i-1}\) 是容易处理的,因为我们什么也不用做,把上一次的区间都延长过来就可以。
-
若 \(y_i<y_{i-1}\),我们不能把所有未确定右端点的区间都接过来,必须要断掉恰好 \(d=y_{i-1}-y_i\) 条边。根据想让最短区间最长的目标,断掉左端点前 \(d\) 小的线段是最优的。所以把左端点前 \(d\) 小的线段右端点设为 \(x_i-1\),把它们移出未确定右端点的区间集合并更新答案。
-
若 \(y_i>y_{i-1}\),那么缺 \(d=y_i-y_{i-1}\) 个区间。令它们左端点最小,则新增 \(d\) 个左端点为 \(x_{i-1}+1\),右端点未确定的区间,加入集合。
由于 \(y\le 10^9\),\(m\) 很大,暴力维护所有左端点不可行。但发现每次我们加入集合的左端点都单调递增,用一个队列存储二元组 \((x,y)\) 表示插入了 \(y\) 条左端点为 \(x\) 的区间。删除的时候弹队首即可,时间复杂度 \(O(n)\)。
点击查看代码
const int N=2e5+5,inf=1e9;
int n,x[N],y[N];
pii q[N];
int st=1,ed=0,ans=inf;
int main()
{
n=read();
for(int i=1;i<=n;i++) x[i]=read();
for(int i=1;i<=n;i++) y[i]=read();
x[0]=-inf;
for(int i=1;i<=n;i++)
{
if(y[i]==y[i-1]) continue;
if(y[i]>y[i-1]) q[++ed]=pii(x[i-1],y[i]-y[i-1]);
else
{
int now=y[i-1]-y[i];
while(st<=ed&&q[st].se<=now)
{
ans=min(ans,x[i]-q[st].fi-1);
now-=q[st].se,st++;
}
if(st<=ed&&now&&q[st].se>now) q[st].se-=now,ans=min(ans,x[i]-q[st].fi-1);
}
}
if(ans==inf) printf("-1\n");
else printf("%d\n",ans-1);
return 0;
}