10-09 周一 图解机器学习之深度学习感知机学习

news2024/9/24 9:27:23
10-09 周一 图解机器学习之深度学习感知机学习
时间版本修改人描述
2023年10月9日14:13:20V0.1宋全恒新建文档

简介

 感知机是神经网络中的概念，1958年被Frank Rosenblatt第一次引入。感知机作为一种基本的神经网络模型，它模拟了人脑神经元的工作原理。感知机接受多个输入信号，将它们加权求和并加上偏置值，然后通过一个激活函数将结果转化为输出信号。感知机能够容易的实现逻辑与，或，非。但单层感知机无法实现异或。

 感知机可以用于分类问题，将输入信号分为不同的类别。

 感知机也是神经网络的基本组成单元，通过感知机的组合可以构建更加复杂的神经网络模型，比如说多层感知机MLP和卷积神经网络CNN。

img

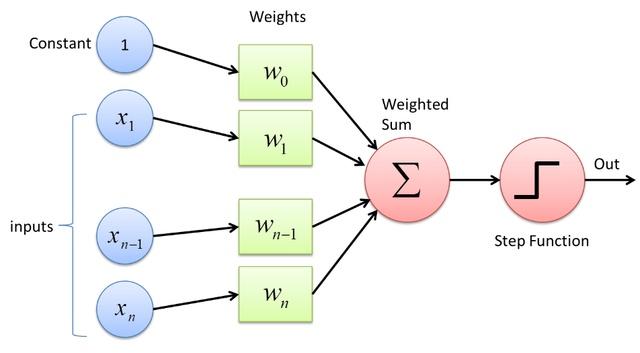
 感知机的基本原理可以用一下公式表示：

img

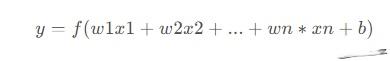
 感知机的学习过程，通过不断调整权重和偏置值来完成，一般采用梯度下降算法，通过最小化损失函数来优化权重和偏置值。常用的损失函数包括均方误差和交叉熵。

概念理解

  • 样本特征矩阵
  • 标签y
  • 训练迭代
    • 将要定义一个训练函数 perceptron，使用变量n_iter表示迭代次数。每迭代一次，感知机会用当前的权重对样本进行预测，并计算预测值与真实标签之间的误差。然后根据误差值来调整权重，以期望能够使预测结果更加接近真实标签。
      n_iter 值越大，训练时间越长，可能会使得感知机的性能提高，但也会增加过拟合的风险。在实际应用中，我们需要根据具体情况来调整 n_iter 的值。
  • 学习率
    • 学习率控制了每次参数更新的步长，即每次参数更新时改变的大小。
    • 在单层感知机中，学习率决定了每次更新权重和偏置的步长。
    • 通常可以使用网格搜索或随机搜索等方法来搜索最优的学习率。另外，还可以使用自适应学习率的方法，如 Adagrad、Adadelta、Adam 等，自动调整学习率大小，以提高模型的训练效果。
  • 计算预测值
  • 更新权重
    • weights = weights + learning_rate * y[i] * X[i]
  • 更新偏置
    • bias = bias + learning_rate * y[i]
  • 绘制决策边界
# error 是误差
error = y - y_pred
weights = weights + learning_rate * error 
Xbias = bias + learning_rate * error

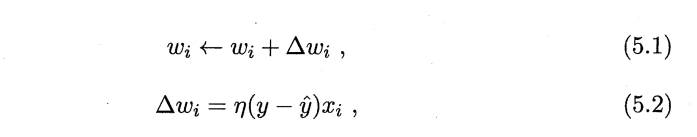
image-20231009163050569

 上图参见机器学习p99

图示

img

 

代码理解

代码

#程序代码13.1 python实现感知器网络，并对and函数训练，名称：Perceptron.py
#coding utf-8
from functools import reduce
 
class perceptron(object):
    #初始化，输入训练数目，激活函数
    def __init__(self,input_num,activator):#activator为激活函数
        self.activator=activator
        self.weights=[0.0 for _ in range(input_num)]#权重初始化为0
        self.bias=0.0#偏置初始化为0.0
    #运算
    def operation(self,input_vec):
        #对激活函数中的参数做运算，x[0]代表input_vec,x[1]代表weights
        #0.0为reduce的初始计算值
        sum=reduce(lambda a,b:a+b,map(lambda x:x[0]*x[1],zip(input_vec,self.weights)),0.0)
        return self.activator(sum+self.bias)
    
    #权值和更新
    def updata(self,input_vec,output,label,rate):
        delta=label-output
        print("label: %d, output: %f, delta: %f" %(label, output, delta))
        self.weights=list(map(lambda x:x[1]+rate*delta*x[0],zip(input_vec,self.weights)))#加上list跟python2有区别
        self.bias+=rate*delta
    
    #训练，输入数据及对应标签，迭代次数，学习率
    def train(self,input_vecs,labels,iteration_num,rate):
        for i in range(iteration_num):#iteration_num次迭代
            samples=zip(input_vecs,labels)#打包
            for (input_vec,label) in samples:
                output=self.operation(input_vec)#计算输出值
                self.updata(input_vec,output,label,rate)#更新
    
    #预测
    def predict(self,input_vec):
        return self.operation(input_vec)
    
    #打印权值，偏置
    def __str__(self):#内部函数
        return "weight: %s, bias: %f"%(self.weights,self.bias)#权值返回用%s
        
'''实现与(and)函数功能'''
#激活函数为阶跃函数
def andActivator(x):
    if x>0:
        return 1
    else:
        return 0
    
#得到训练数据
def getTrainData():
    input_vecs=[[1,1],[1,0],[0,1],[0,0]]#可重用多次循环迭代
    labels=[1,0,0,0]
    return input_vecs,labels
#训练感知机
def trainPerceptron():
    p=perceptron(2,andActivator)
    input_vecs,labels=getTrainData()
    p.train(input_vecs,labels,100,0.1)#100为迭代次数，0.1为学习率
    return p
#主函数
if __name__=='__main__':
    train_perceptron=trainPerceptron()
    print(train_perceptron)
#测试
    print('感知器训练网络，训练布尔And函数')
    print('1 and 1 = %d' % train_perceptron.predict([1,1]))
    print('1 and 0 = %d' % train_perceptron.predict([1,0]))
    #print("0 and 1 =%d"%train_perceptron.predict([0,1]))
    print('0 and 1 = %d' % train_perceptron.predict([0,1]))
    print('0 and 0 = %d' % train_perceptron.predict([0,0]))
    # 测试
   # print '1 and 1 = %d' % and_perception.predict([1, 1])
   # print '0 and 0 = %d' % and_perception.predict([0, 0])
   # print '1 and 0 = %d' % and_perception.predict([1, 0])
   # print '0 and 1 = %d' % and_perception.predict([0, 1])

流程

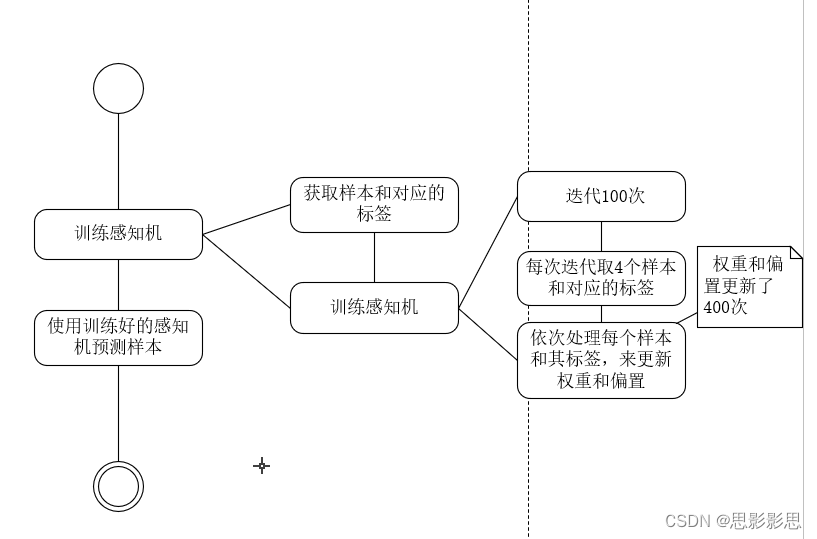
在这里插入图片描述

代码片段理解

operation

    #运算
    def operation(self,input_vec):
        #对激活函数中的参数做运算，x[0]代表input_vec,x[1]代表weights
        #0.0为reduce的初始计算值
        sum=reduce(lambda a,b:a+b,map(lambda x:x[0]*x[1],zip(input_vec,self.weights)),0.0)
        return self.activator(sum+self.bias)

 上述首先是sum，`map(lambda x:x[0]*x[1],zip(input_vec,self.weights))``````

权重更新

    #权值和更新
    def updata(self,input_vec,output,label,rate):
        delta=label-output
        print("label: %d, output: %f, delta: %f" %(label, output, delta))
        self.weights=list(map(lambda x:x[1]+rate*delta*x[0],zip(input_vec,self.weights)))#加上list跟python2有区别
        self.bias+=rate*delta

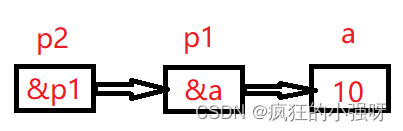
注： 该感知机两个节点，因此有两个权重值，对于数据[[1,1],[1,0],[0,1],[0,0]]，中的每一个样本,以[1, 1]， 对应的两个权重为w1，w2；

 在update函数中，input_vec仅仅代表一个样本，如[1, 1].

 在每个样本更新时，权重wi只与样本中第i个属性xi有关。具体更新的过程可以参见下图：

 具体可参见下属更新日志：

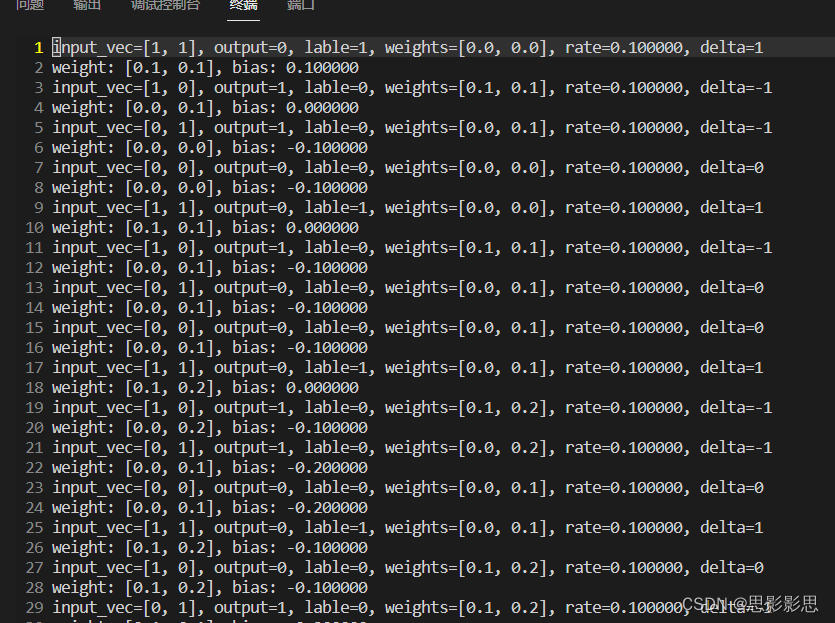
在这里插入图片描述

 参考下面的数据变化

(base) root@node33-a100:/home/sqh/deep# cat log | head -n 10
input_vec=[1, 1], output=0, lable=1, weights=[0.0, 0.0], rate=0.100000, delta=1
weight: [0.1, 0.1], bias: 0.100000
input_vec=[1, 0], output=1, lable=0, weights=[0.1, 0.1], rate=0.100000, delta=-1
weight: [0.0, 0.1], bias: 0.000000
input_vec=[0, 1], output=1, lable=0, weights=[0.0, 0.1], rate=0.100000, delta=-1
weight: [0.0, 0.0], bias: -0.100000
input_vec=[0, 0], output=0, lable=0, weights=[0.0, 0.0], rate=0.100000, delta=0
weight: [0.0, 0.0], bias: -0.100000
input_vec=[1, 1], output=0, lable=1, weights=[0.0, 0.0], rate=0.100000, delta=1
weight: [0.1, 0.1], bias: 0.000000

10-09 周一 感知机理解计算过程

 而偏置的学习，相当于权重的更新，只不过对应的特征值始终为1.理解参见下图机器学习第99页：

image-20231009211755573

即感知机中偏置的学习公式如下：

在这里插入图片描述

训练的过程

    #训练，输入数据及对应标签，迭代次数，学习率
    def train(self,input_vecs,labels,iteration_num,rate):
        for i in range(iteration_num):#iteration_num次迭代
            samples=zip(input_vecs,labels)#打包
            for (input_vec,label) in samples:
                
                output=self.operation(input_vec)#计算输出值
                # print("output=", output)
                self.updata(input_vec,output,label,rate)#更新

 上述代码中，训练的过程，可以看到for循环迭代的次数由外部参数传递，本程序中为100，然后，在100次迭代中，每次迭代都把训练数据全部重新执行了一遍，对于每个样本和标签，均更新一次weights和bias。

难点

reduce

 该函数不是Python内置函数，需要通过from functools import reduce 导入。Reduce从序列数据结构返回单个输出值，它通过应用一个改定的函数来减少元素。

reduce(function, sequence[, initial]) -> value

 将包含两个参数的函数(function)累计应用于序列(sequence)的项，从左到右，从而将序列reduce至单个值。

 假设有一个整数列表，并求得所有元素的总和。且使用reduce函数而不是使用for循环来处理此问题。

from functools import reduce
lst = [2,4,6,8,10]
print(reduce(lambda x, y: x+y, lst))
>>> 30

 也可以使用reduce函数而非for循环从列表中找到最大或最小的值：

lst = [2,4,6,8]
# 找到最大元素
print(reduce(lambda x, y: x if x>y else y, lst))
# 找到最小元素
print(reduce(lambda x, y: x if x<y else y, lst))

lambda

 参见 Lambda函数简介

Lambda函数也被称为匿名(没有名称)函数，它直接接受参数的数量以及使用该参数执行的条件或操作，该参数以冒号分隔，并返回最终结果。为了在大型代码库上编写代码时执行一项小任务，或者在函数中执行一项小任务，便在正常过程中使用lambda函数。

lambda argument_list: expression

 其中，argument_list表示参数列表，expression是一个关于参数的表达式，表达式中出现的参数需要在argument_list中有定义，并且表达式只能是单行的。

 lambda是定义函数的一种简单的方法，因此可以给它一个名称，像普通函数一样使用它。

 Lambda是一种不需要名字即标识符，有一个单独的表达式组成的匿名内联函数，表达式会在调用时被求职。

任何能够使用它们的地方，都可以定义一个单独的普通函数来进行替换。我将它们用在需要封装特殊的**、非重用**代码上，避免令我的代码充斥着大量单行函数。

def f(x):
    return x**2
print f(4)

 使用lambda表达式，如下所示：

g = lambda x : x**2
g(4)

 上述同样定义了一个函数，并且命名为g，lmbda 后的变量表示参数，: 后的内容代表返回的值。

Type "help", "copyright", "credits" or "license" for more information.
>>> g = lambda x : x**2
>>> g(5)
25
>>> g(4)
16
>>> g(3)
9

 使用def关键字构建的普通函数返回值或序列数据类型，但在Lambda函数中返回一个完整的过程。假设我们想要检查数字是偶数还是奇数，使用lambda函数语法类似于下面的代码片段。

b = lambda x: "Even" if x%2==0 else "Odd"
b(9)

 普通函数与Lambda函数的区别如下：

  • 没有名称
  • Lambda函数没有返回值
  • 函数只在一行中
  • 不用于代码重用

 一般情况下，我们不使用Lambda函数，而是将其与高阶函数一起使用。高阶函数是一种需要多个函数来完成任务的函数，或者当一个函数返回任何另一个函数时，可以选择使用Lambda函数。

 通过一个例子来理解高阶函数。假设有一个整数列表，必须返回三个输出。

  • 一个列表中所有偶数的和
  • 一个列表中所有奇数的和
  • 一个所有能被三整除的数的和
def return_sum(func, lst):
  result = 0
  for i in lst:
    #if val satisfies func
    if func(i):
      result = result + i
  return result
lst = [11,14,21,56,78,45,29,28]
x = lambda a: a%2 == 0
y = lambda a: a%2 != 0
z = lambda a: a%3 == 0

print(return_sum(x, lst))
print(return_sum(y, lst))
print(return_sum(z, lst))

map

 map() 会根据提供的函数对指定序列做映射

 Map函数是一个接受两个参数的函数。第一个参数 function 以参数序列中的每一个元素调用 function 函数，第二个是任何可迭代的序列数据类型。返回包含每次 function 函数返回值的新列表。

map(function, iterable, ...)

 Map函数将定义在迭代器对象中的某种类型的操作。假设我们要将数组元素进行平方运算，即将一个数组的每个元素的平方映射到另一个产生所需结果的数组。

arr = [2,4,6,8] 
arr = list(map(lambda x: x*x, arr)) 
print(arr)
[4, 16, 36, 64]

 再一个例子：

students = [
            {"name": "John Doe",
             "father name": "Robert Doe",
             "Address": "123 Hall street"
             },
            {
              "name": "Rahul Garg",
              "father name": "Kamal Garg",
              "Address": "3-Upper-Street corner"
            },
            {
              "name": "Angela Steven",
             "father name": "Jabob steven",
             "Address": "Unknown"
            }
]
print(list(map(lambda student: student['name'], students)))
>>> ['John Doe', 'Rahul Garg', 'Angela Steven']

 上述操作通常出现在从数据库或网络抓取获取数据等场景中。

Python map函数是允许你使用一个函数转换整个可迭代对象的函数。这里的关键概念是转换，它可以包括但不限于：

  • 将字符串转换为数字
  • 四舍五入数字
  • 获取每个可迭代项的长度

Filter函数

 Filter函数根据给定的特定条件过滤掉数据。即在函数中设定过滤条件，迭代元素，保留返回值为True 的元素。Map 函数对每个元素进行操作，而 filter 函数仅输出满足特定要求的元素。

filter(function or None, iterable) --> filter object

>>> fruits = ['mango', 'apple', 'orange', 'cherry', 'grapes'] 
>>> print(list(filter(lambda fruit: 'g' in fruit, fruits)))
['mango', 'orange', 'grapes']

zip

zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。

如果各个迭代器的元素个数不一致，则返回列表长度与最短的对象相同，利用 * 号操作符，可以将元组解压为列表。

>>> a = [1,2,3]
>>> b = [4,5,6]
>>> c = [4,5,6,7,8]
>>> zipped = zip(a,b)     # 返回一个对象
>>> zipped
<zip object at 0x103abc288>
>>> list(zipped)  # list() 转换为列表
[(1, 4), (2, 5), (3, 6)]
>>> list(zip(a,c))              # 元素个数与最短的列表一致
[(1, 4), (2, 5), (3, 6)]

>>> a1, a2 = zip(*zip(a,b))          # 与 zip 相反，zip(*) 可理解为解压，返回二维矩阵式
>>> list(a1)
[1, 2, 3]
>>> list(a2)
[4, 5, 6]
>>>

 正确的理解zip()对于updata函数的理解非常重要

    #权值和更新
    def updata(self,input_vec,output,label,rate):
        delta=label-output
        #print("label: %d, output: %f, delta: %f" %(label, output, delta))
        print("input_vec=%s, output=%d, lable=%d, weights=%s, rate=%f, delta=%d" %(input_vec, output, label, self.weights, rate, delta))
        self.weights=list(map(lambda x:x[1]+rate*delta*x[0],zip(input_vec,self.weights)))
       
        self.bias+=rate*delta
        print(self)

总结

 最近感觉自己，心浮气躁的，非常不舒服，还是要不断地学习才能不断的丰富和充实自己。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1074905.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

解决Feign的自定义解码器在接口返回值为void时不执行的问题

解决Feign的自定义解码器在接口返回值为void时不执行的问题

项目的接口有一个全局的响应包装器&#xff0c;将接口的所有返回&#xff0c;包括各种类型如List、Entity&#xff0c;或者void&#xff0c;以及抛出的异常&#xff0c;封装成统一的结构给到前端&#xff0c;所以在使用Feign发起远程调用的时候&#xff0c;需要一个自定义的解码…
阅读更多...
详解 ElasticSearch 基础教程

详解 ElasticSearch 基础教程

&#x1f339; 分享 ElasticSearch 基础&#xff0c;请指教。&#x1f339;&#x1f339; 如你对技术也感兴趣&#xff0c;欢迎交流。&#x1f339;&#x1f339;&#x1f339; 如有对阁下帮助&#xff0c;请&#x1f44d;点赞&#x1f496;收藏&#x1f431;‍&#x1f3cd;分…
阅读更多...
Python 自动化Web测试

Python 自动化Web测试

限于作者水平有限&#xff0c;以下内容可能是管窥之见&#xff0c;希望大家高抬贵手&#xff0c;且让我斗胆抛砖引玉。 公司产品迪备主要是通过网页操作来进行数据库的备份与恢复&#xff0c;监控与管理&#xff0c;因此在测试的过程中&#xff0c;可以用python测试脚本来模拟…
阅读更多...
运维知识点汇总

运维知识点汇总

一.公共基础 linux常用目录 链接一 链接二 linux系统启动 链接一 链接二 LVM 链接一 磁盘挂载 链接一 文件权限 链接一 二.VLAN详解 链接 三.中间件 单体部署&#xff1a; 优点&#xff1a; &#xff08;1&#xff09;小团队成型即可完成开发-测试-上线&am…
阅读更多...
3D机器视觉：解锁未来的立体视野

3D机器视觉：解锁未来的立体视野

原创 | 文 BFT机器人 机器视觉领域一直在不断演进&#xff0c;从最初的二维图像处理&#xff0c;逐渐扩展到了更复杂的三维领域&#xff0c;形成了3D机器视觉。3D机器视觉技术的涌现为计算机系统带来了全新的感知和理解能力&#xff0c;这一领域的发展正日益受到广泛关注。本文…
阅读更多...
Android系统为什么采用Binder作为IPC机制

Android系统为什么采用Binder作为IPC机制

Android系统提供了多种进程间通信&#xff08;IPC&#xff09;的机制&#xff0c;用于不同进程之间的数据交换和通信。以下是Android系统中常用的几种IPC机制&#xff1a; Intent&#xff1a;Intent是Android系统中常用的一种进程间通信方式。通过发送Intent&#xff0c;可以在…
阅读更多...
链表去重Java

链表去重Java

去除掉链表中重复的元素,两种方法: static class ListNode{private int val;private ListNode next;public ListNode(int val, ListNode next) {this.val val;this.next next;}Overridepublic String toString() {return "ListNode{" "val" val ",…
阅读更多...
【jvm】程序计数器

【jvm】程序计数器

目录 一、介绍二、作用三、示例3.1 代码3.2 javap -v Test1.class3.2.1 操作指令及地址 一、介绍 1.jvm中的程序计数寄存器中&#xff08;program counter register&#xff09;&#xff0c;register的命名源于cpu的寄存器&#xff0c;寄存器存储指令相关的现场信息 2.cpu只有把…
阅读更多...
C++学习之指针和数组

C++学习之指针和数组

指针和一维数组 一个数组包含若干元素&#xff0c;每个数组元素都在内存中占用存储单元&#xff0c;它们都有相应的地址。指针变量既可以指向变量&#xff0c;当然也可以指向数组元素。所谓数组元素的指针就是数组元素的地址。 eg&#xff1a; int a[6]; //定义一个整数数组a…
阅读更多...
web：[HCTF 2018]admin

web：[HCTF 2018]admin

题目 点击页面显示如下 点击hctf显示 没有账号&#xff0c;先注册一个 随便注册一个试试看 输入账号密码显示如下 页面没有其他的提示&#xff0c;查看源代码 这里提示不是admin 先注册一个admin账号试一下 显示admin已经被注册了&#xff0c;所以知道用户名为admin&#xff0…
阅读更多...
【图像分割】SAM、FastSAM与MobileSAM原理

【图像分割】SAM、FastSAM与MobileSAM原理

文章目录 前言&#xff1a;Segment Anything一、FastSAM二、MobileSAM框架实验 总结 前言&#xff1a;Segment Anything Meta 今年发布了图像分割模型 Segment Anything Model (SAM) 。SAM 已经学会了关于物体的一般概念&#xff0c;可以为任何图像或视频中的任何物体生成 mas…
阅读更多...
基于共生生物优化的BP神经网络（分类应用） - 附代码

基于共生生物优化的BP神经网络（分类应用） - 附代码

基于共生生物优化的BP神经网络&#xff08;分类应用&#xff09; - 附代码 文章目录 基于共生生物优化的BP神经网络&#xff08;分类应用&#xff09; - 附代码1.鸢尾花iris数据介绍2.数据集整理3.共生生物优化BP神经网络3.1 BP神经网络参数设置3.2 共生生物算法应用 4.测试结果…
阅读更多...
JDBC-day03(BLOB类型字段，批量插入)

JDBC-day03(BLOB类型字段，批量插入)

四&#xff1a;操作BLOB类型字段 1.MySQL BLOB类型 在MySQL中&#xff0c;BLOB是一个二进制大型对象&#xff0c;是一个可以存储大量数据的容器&#xff0c;它能容纳不同大小的数据。可以用来存储图片&#xff0c;视频等 插入BLOB类型的数据必须使用PreparedStatement&#x…
阅读更多...
redis,mongoDB,mysql,Elasticsearch区别

redis,mongoDB,mysql,Elasticsearch区别

Redis&#xff1a; Redis是一种高性能键值存储数据库&#xff0c;基于内存操作&#xff0c;支持数据持久化&#xff0c;支持数据类型丰富灵活&#xff0c;如字符串、哈希、列表、集合、有序集合等。Redis还提供了订阅/发布、事务、Lua脚本、主从同步等功能&#xff0c;适用于访…
阅读更多...
学习记忆——数学篇——案例——代数——函数——一元二次函数

学习记忆——数学篇——案例——代数——函数——一元二次函数

记忆宫殿法 一元二次函数&#xff1a; y a x 2 b x c yax^2bxc yax2bxc a &#xff1e; 0 a&#xff1e;0 a&#xff1e;0&#xff0c;开口向上&#xff1b; a &#xff1c; 0 a&#xff1c;0 a&#xff1c;0&#xff0c;开口向下&#xff1b; x − b 2 a x-\frac{b}{2a…
阅读更多...
2023-10-09 python-使用psd_tools-读取psd信息及导出图层图片-记录

2023-10-09 python-使用psd_tools-读取psd信息及导出图层图片-记录

摘要: 2023-10-09 python-使用psd_tools-读取psd信息及导出图层图片-记录 相关文档: Usage — psd-tools 1.9.28 documentation 读取psd的信息: py代码: from psd_tools import PSDImagepsd PSDImage.open(example.psd) #psd PSDImage.open(one.psd)print(psd)for layer in …
阅读更多...
DirectX C++项目调试时报错：The FX file cannot be complied.

DirectX C++项目调试时报错：The FX file cannot be complied.

文章目录 遇到的问题错误排除方法经验总结 遇到的问题 在编虚拟现实的课程作业的时候&#xff0c;打算基于上一次的作业项目改一改来交&#xff0c;于是把上次项目的代码复制过来。生成解决方案的过程没有报错&#xff0c;但是在调试该项目时&#xff0c;报错内容如下图所示&a…
阅读更多...
vulnhub_clover靶机渗透测试

vulnhub_clover靶机渗透测试

clover靶机 文章目录 clover靶机信息收集ftp渗透web渗透横线移动权限提升靶机总结 靶机地址&#xff1a;https://www.vulnhub.com/entry/clover-1,687/ 信息收集 使用nmap扫描得到了很对端口&#xff0c;能用的也就是21 22 80三个端口&#xff0c;其他都是关闭的&#xff0c;全…
阅读更多...
【开发篇】二十三、SpringBoot Admin端点指标控制以及自定义端点

【开发篇】二十三、SpringBoot Admin端点指标控制以及自定义端点

文章目录 1、info端点指标控制2、health端点指标控制3、metrics端点指标控制4、自定义端点5、补充 接上篇&#xff0c;整合完SpringBoot Admin的客户端和服务端后&#xff0c;在监控页面看到信息栏是空的&#xff0c;但info端点是开放的&#xff0c;这就涉及到端点指标控制。 1…
阅读更多...
基于ffmpeg给视频添加时间字幕

基于ffmpeg给视频添加时间字幕

FFmpeg是一套可以用来记录、转换数字音频、视频&#xff0c;并能将其转化为流的开源计算机程序&#xff0c;我们可以基于ffmpeg对视频进行各种操作。本文主要介绍基于ffmpeg给视频添加字幕&#xff0c;字幕的内容为视频所播放的时间&#xff08;故需要安装ffmpeg&#xff0c;具…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023