题目一
试题编号: 202012-1
试题名称: 期末预测之安全指数
时间限制: 1.0s
内存限制: 512.0MB

题目分析(个人理解)
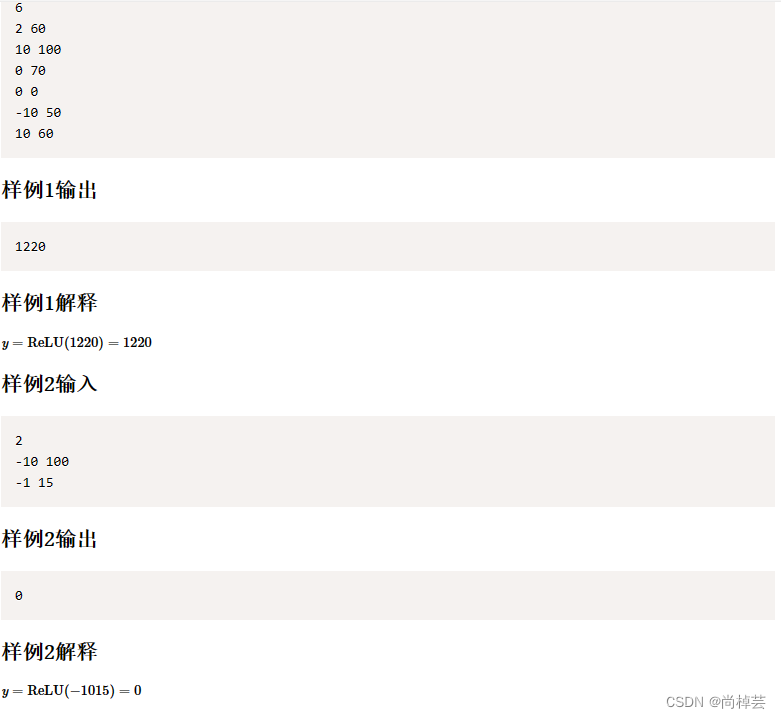
- 还是先看输出,此题简单的离谱,第一行输入小菜有几个测评依据,然后后面的n行输入每项测评依据的重要度,和分数。
- 再看输出,那个 RELU函书其实就是输出:如果总分大于0就输出分数,如果小于或等于0就输出0即可。
- 代码如下!!!
n=int(input())
num=0
for i in range(n):
w,score=map(int,(input().split()))
num+=w*score
if num>0:
print(num)
else:
print(0)
题目二
试题编号: 202012-2
试题名称: 期末预测之最佳阈值
时间限制: 1.0s
内存限制: 512.0MB


题目分析(个人理解)
- 先看输入第一行是输入有n需要判断预测是否正确的数,之后的n行输入对应的yi和result i 。
- 我依旧选择列表存储,字典的keys必须为一,将yi 或result i作为keys都不 满足条件。for i in range(m):
y_result.append(list(map(int,input().split()))) - 然后先按照reslut降序排列,再按照yi升序排列,之后到核心代码去判断每一个y作为阈值之后,预测正确的有几项,预测正确的情况有两种,第一种是大于等于yi的reslut值为1。第二种是小于yi的result值为0。这两种分别判断然后计数再相加存在列表中,列表中每个值表示当前位序对应的yi作为阈值时预测正确的个数。将该列表倒序输出,保证出现相同的正确次数时输出较大的y。
- 具体如何判断?
# 构建存储predict正确数量的列表
count_Ture = []
# 正序遍历计算所有元素位置前 0 的个数(预测正确)
count = 0
for i in range(m):
count_Ture.append(count)
if y_result[i][1] == 0:
count += 1
# 倒序遍历计算所有元素位置后 1 的个数(预测正确)
count = 0
for i in range(m-1,-1,-1):
if y_result[i][1] == 1:
count += 1
count_Ture[i] += count
- 就是排序之后,第一个循环是将当前遍历到的安全指数设为阈值,因为阈值等于自身时,预测结果为1,所以需要先将预测正确结果保存下来再做判断使count+1。count之所以在result为0时自加1,是因为通过以安全指数(yi)排序之后,之后的安全指数都是大于之前的,所以之后的安全指数(作阈值时)在检测排序在其之前的且result为0的数据时一定检测成功,所以使count+1。倒序遍历则原理相同只是计算时,因为当前安全指数检测自身这组数据时一定相等,所以当result为1时先做count+1的操作再进行保存。(倒序遍历时是小于本次遍历到的安全指数作为阈值时,本次遍历的这组数据若result为1,则必检测过)。
- 上完整代码!!!
# 输入安全指数数量
m = int(input())
# 初始化 y,result 存储列表
y_result = []
# 循环输入 y,result
for i in range(m):
y_result.append(list(map(int,input().split())))
# 先按照result排序再按照y排序 避免使用同一y的最大predict
y_result.sort(key=lambda x:x[1],reverse=True)
y_result.sort(key=lambda x:x[0])
# 构建存储predict正确数量的列表
count_Ture = []
# 正序遍历计算所有元素位置前 0 的个数(预测正确)
count = 0
for i in range(m):
count_Ture.append(count)
if y_result[i][1] == 0:
count += 1
# 倒序遍历计算所有元素位置后 1 的个数(预测正确)
count = 0
for i in range(m-1,-1,-1):
if y_result[i][1] == 1:
count += 1
count_Ture[i] += count
# 存储predict正确数量列表倒序操作(保证相同predict时输出y较大的) 并计算最大正确数量的下标索引
count_Ture.reverse()
index = m - 1 - count_Ture.index(max(count_Ture))
# 输出最佳阈值
print(y_result[index][0])
总结
跑步跑步跑步!何惧风雨?跑完我发截图到评论区。