一、回溯思路及模板
1、如果解决一个问题有多个步骤,每一个步骤有多种方法,题目又要我们找出所有的方法,可以使用回溯算法;
回溯算法是在一棵树上的 深度优先遍历(因为要找所有的解,所以需要遍历);
2、回溯算法首先需要画出递归树,不同的树决定了不同的代码实现。下面给出了两种画树的思路。!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
2、模板
解释:回溯算法中函数返回值一般为void。
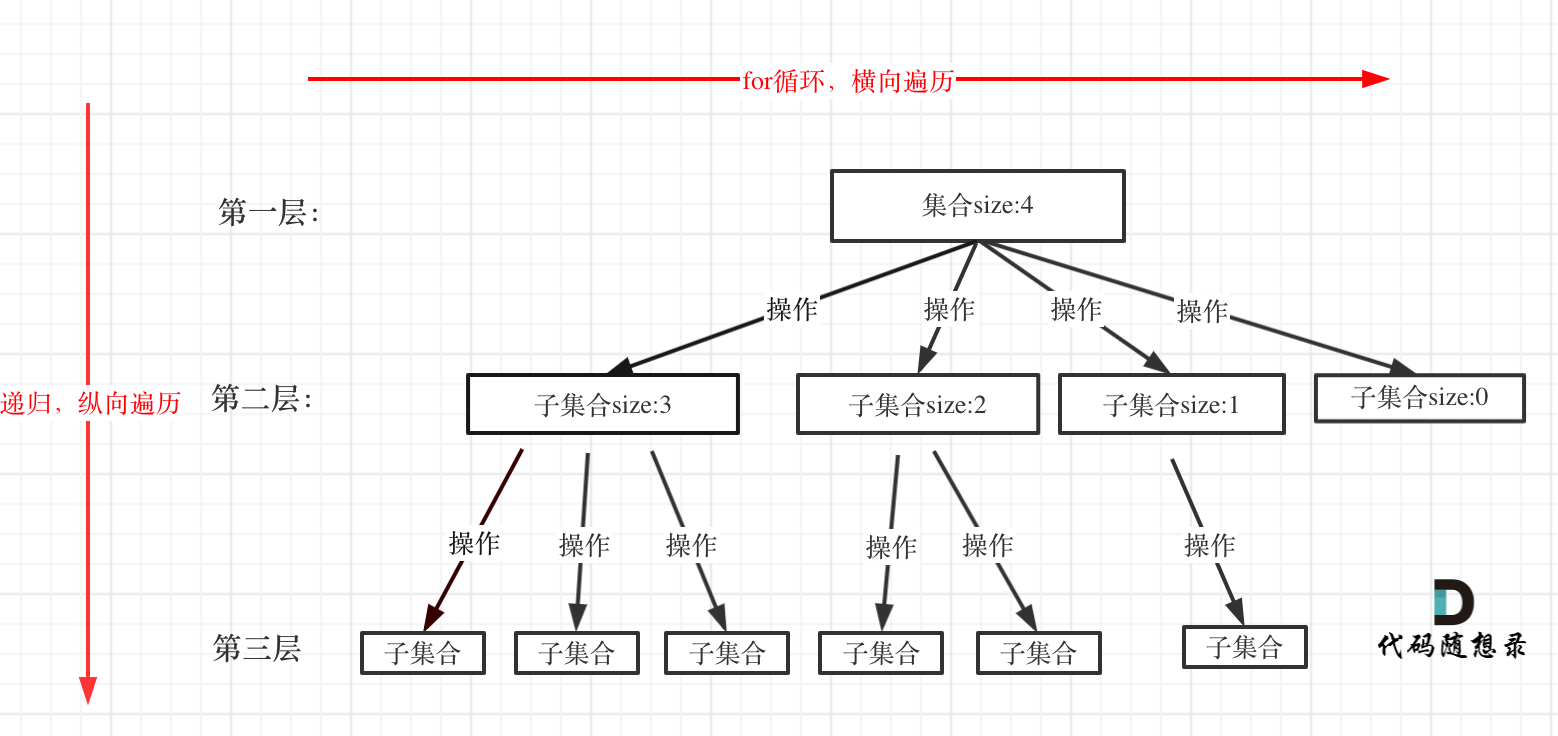
集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
void backtracking(参数) { //参数一般边写边添加,一开始不能全部确定
if (终止条件) { //一般为空
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { //for循环横向遍历,遍历n叉树的所有孩子。
处理节点;
backtracking(路径,选择列表); // 递归 :纵向遍历
回溯,撤销处理结果
}
}如图:回溯算法首先需要画出递归树,不同的树决定了不同的代码实现。下面给出了两种画树的思路。
二、剪枝
1、减宽度,就是舍弃掉当前层的有些元素(组合问题),如果,后面的元素个数,已经不够 题目要求的个数,直接return
2、减深度,若题目类型是带 和 等一些条件的约束(组合求和),如果遍历到该元素, 和 已经不满足条件了,就直接return