1、相关定义

• 过参数化：主要是指在训练阶段，在数学上需要进行大量的微分求解，去捕捉数据中微小的变化信息，一旦完成迭代式的训练之后，网络模型在推理的时候就不需要这么多参数。
• 剪枝算法：核心思想就是减少网络模型中参数量和计算量，同时尽量保证模型的性能不受影响。

2、剪枝步骤

对模型进行剪枝常用的三种方法：
（1）训练好一个模型-》对模型进行剪枝-》对剪枝后的模型进行微调
（2）在模型训练过程中进行剪枝-》剪枝后模型进行微调
（3）进行剪枝-》从头训练剪枝后模型
训练-》剪枝-》微调

非结构化剪枝
主要对一些独立的权重或者神经元进行剪枝，是粒度最小的剪枝。
最简单的方法是预定义一个阈值，低于这个阈值的权重被减去，高于的被保留。所存在的三个主要缺点：
1.阈值与稀疏性没有直接联系
2.不同的层应该具有不同的灵敏度
3.这样设置阈值可能会剪掉太多信息，无法恢复原来的精度
优点：剪枝算法简单、模型压缩比高
缺点：精度不可控，剪枝后权重矩阵稀疏，没有专用硬件难以实现压缩和加速的效果
结构化剪枝
结构化的剪枝是有规律、有顺序的。对神经网络，或者计算图进行剪枝，经典对layer剪枝，channel剪枝以及对filter剪枝，剪枝粒度依次增大。
优点：大部分算法保留原始卷积结构，不需要专用硬件就可以实现
缺点：剪枝算法相对复杂

软剪枝
硬剪枝

3、什么是通道剪枝

论文：Channel Pruning for Accelerating Very Deep Neural Networks
论文链接：https://arxiv.org/abs/1707.06168
代码地址：https://github.com/yihui-he/channel-pruning
这是一篇ICCV2017的文章，关于用通道剪枝channel pruning来做模型加速，通道剪枝是模型压缩和加速领域的一个重要分支。

文章的核心内容是对训练好的模型进行通道剪枝，其通过迭代两部操作进行：
（1）channel selection
这一步采用LASSO regression来进行的，通过添加一个L1范数来约束权重，因为L1范数可以使得权重中大部分值为0，所以能够使得权重更加稀疏。这样就能够把稀疏的channel剪掉；
（2）reconstruction
这一步是基于linear least squares也就是最小二乘来约束剪枝后输出的feature map要尽可能和剪枝前的输出feature map相等，也就是最小二乘值越小越好。

本文采用的通道剪枝（channel pruning）是模型压缩和加速领域中一种简化网络结构的操作，文中作者还列举了其他两种常见的简化网络结构的操作：sparse connection和tensor factorization，可以看Figure1的对比。
（a）表示传统的3层卷积操作。
（b）表示sparse connection，这是通过去掉一些参数很小的连接得到的，理论上是有明显的加速效果的，但是在实现过程中并不容易，主要因为稀疏连接层的形状不规则。
（c）表示tensor factorization，比如SVD分解，但是这种操作其实并不会减少channel数量，因此很难带来明显加速。
（d）就是通道剪枝（channel pruning），也就是直接对channel做剪枝，移除掉一些冗余的channel，相当于给网络结构瘦身，而且各个卷积层的形状还比较统一。

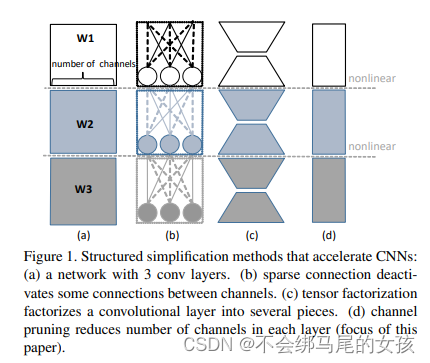
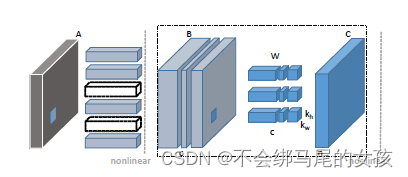
图2是本文对于卷积层做通道剪枝的一个示意图，
通过左边大的虚线框，其中

• 字母B表示输入feature map,同时c表示B的通道数量；
• 字母W表示卷积核，卷积核的数量是n，每个卷积核的维度是ckhkw,kh和kw表示卷积核的size;
• 字母C表示输出feature map，通道数是n
  因此通道剪枝的目的是要把B中的某些通道剪掉，使得剪掉后的B和W的卷积结果能尽可能和C接近。
  要剪掉B中的一些feature map的通道时，相当于剪掉了W中与这些通道对应的卷积核（对应W中3个最小的立方体块），这也是后面要介绍的公式中β的含义和之所以用L1范数来约束β的原因，因为L1范数会使得W更加稀疏。另外生成这些被剪掉通道的feature map的卷积核也可以删掉（对应Figure2中第二列的6个长条矩形块中的2个黑色虚线框的矩形块）。
  
  参考：
  https://zhuanlan.zhihu.com/p/609126518
  https://blog.csdn.net/librahfacebook/article/details/97552163