算法通过村第十三关-术数|白银笔记|术数高频问题

文章目录

前言
数组实现加法专题
- 数组实现整数加法
- 字符串加法
- 二进制加法
幂运算专题
- 求2的次幂
- 求3的次幂
- 求4的次幂
总结

前言

提示：人心本易趋死寂，苦难之后，焕然重建，激荡一阵，又趋麻木。 --苏枕书《有鹿来》

我们继续看几个数学与数字相关的重要题目，数学的问题有很多，力扣上面也有很多练习，通过这些练习你可以掌握很多技巧，真的如果你不练习，你真的不知道其实还可以这么做。所以算法也是一个累计的过程，积累经验才能以后游刃有余。

数组实现加法专题

数字加法，可以说是老生常谈了，但是让你用数组表示一个数，你需要如何去实现呢？今天我们就来挑战一下。

这里提前说一下，你会遇到很多棘手的问题，例如：A[0]位置时发现如果进位要怎么办？

再拓展一下，如果给定两个数，一个数用数组存储，另外一个是普通的整数，又该如何处理呢？

在拓展，如果两个整数是用字符串表示的呢？如果是二进制表示的呢？加法的规则怎么处理？

数组实现整数加法

参考题目介绍：66. 加一 - 力扣（LeetCode）

在这里插入图片描述

这个看似很简单？从后向前一次加就行了，如果有进位就标记一下，但是如果到头了也要进位要怎么办？

例如：digits=[9,9,9]，从后面向前加的时候，到了A[0]的位置计算为0，需要再次进位，但是数组却不能保存，这里该怎么办？

这里的关键是A[0] 在什么时候出现进位的情况，我们直到此时一定是9， 99， 999， …这样的结构才会出现加1之后再次进位，而进位之后的结果一定是10，100，1000这样的结构，由于Java中数组默认初始化为0，所以我们此时只需要再次申请一个空间比A[]大一个数的数组B[],然后将B[0]设置为1就可以。代码写起来也很简洁。

   /**
    * 整数加一
    * @param digits
    * @return
    */
   public static int[] plusOne(int[] digits) {
       int len = digits.length;
       for (int i = len - 1; i >= 0; i--) {
           digits[i]++;
           digits[i] %= 10;
           // 注意这里 提前出去的条件
           if (digits[i] != 0) {
               return digits;
           }
       }
       // 9 99 999等 // 这里比较巧妙
       digits = new int[len + 1];
       digits[0] = 1;
       return digits;

   }

字符串加法

我们继续看将数组存储再字符串中的情况：字符串加法就是使用字符串表示数字，然后计算他们的和。具体要求如下：给定两个字符串形式的非负整数num1和num2，计算他们的和并同样以字符串形式返回。你不能使用内建的用于处理大整数的库（比如BigInteger），也不能直接将输入的字符串转换成整数形式。

我们写个例子：

例如：
输入：num1 = "456" , num2 = "77"
输出："533"

我们先想一下小学里面的加法是如何实现两个数的计算的。经典的竖式加法：
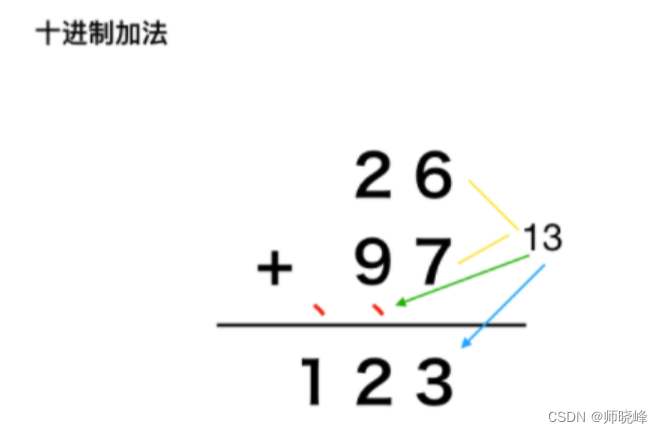
在这里插入图片描述
从低位到高位逐步相加，如果当前位和超过10，则向高位进一位。

因此我们只要将这个过程用代码表示出来就可以了。先定义两个指针 i 和 j 分别指向 num1 和num2 的末尾，也就是最低位，同样定义一个变量 add 维护当前是否需要进位，然后从末尾到开头诸位累加。

这里有个问题，两个数字位数不同该怎么处理？很简单，补0就可以了，我们看看具体要怎么做吧：

    /**
     *  两个字符串相加
     * @param num1
     * @param num2
     * @return
     */
    public static String addStrings(String num1, String num2) {
        // 准备工作
        int len1 = num1.length(), len2 = num2.length();
        StringBuffer ans = new StringBuffer();
        int add = 0;
        // 注意循环条件处理
        while(len1 >= 0||len2 >= 0 || add != 0){
            // 缺位补0
            int x = len1 >= 0 ? num1.charAt(len1) - '0' : 0;
            int y = len2 >= 0 ? num2.charAt(len2) - '0' : 0;
            int result = x + y + add;
            ans.append(result % 10);
            add = result / 10;
            len1--;
            len2--;
        }
        // 计算完毕后记得反转
        ans.reverse();
        return  ans.toString();
    }

二进制加法

参考题目介绍：67. 二进制求和 - 力扣（LeetCode）

在这里插入图片描述

我们看看二进制怎么处理吧！这个题目也是用字符串表示数据的，也要先转为字符数组。我们熟悉的十进制，是从个位开始，逐步到高位，达到10就进位，而对于二进制判断相加之后是否为2，就可以决定是否发生进位了。如果是就进位。所以思路大致一样，也是由于字符串的操作原因，不确定左后移位是否出现进位，这里提供两个办法处理

第一种：在进行计算时直接拼接字符串，得到一个反向字符，最后再翻转回来。（10进制一样）
第二种：按照位置给结果字符赋值，最后如果有进位，则在前方进行字符串拼接加进位

我们这里就采用第二种做：

    /**
     * 两个字符串二进制相加
     * @param a
     * @param b
     * @return
     */
    public static String addBinary(String a, String b) {
        // 准备工作
        int len1 = a.length(), len2 = b.length();
        StringBuffer ans = new StringBuffer();
        int add = 0;
        for (int i = len1 - 1, j = len2 - 1; i >= 0 || j >= 0; i--, j--) {
            int sum = add;
            sum += i >= 0 ? a.charAt(i) - '0' : 0;
            sum += j >= 0 ? b.charAt(j) - '0' : 0;
            ans.append(sum % 2);
            add = sum / 2;
        }
        ans.append(add == 1 ? add : "");
        return ans.reverse().toString();
    }

当然有人回想，这里转成十进制，计算完成后再转成二进制不也行吗？这么实现很容易，而且可以使用语言的特性直接转换，但是面试的时候也不行，用不了，但是工程里可以这么做，稳定（算法不行，不能这么干）

幂运算专题

幂运算也是常见的数学运算，其形式为a^{b，也就是a的b次方呗，其中a称为底数，b称为指数，a}b的合法运算（不会出现a == 0 且 b <= 0 的情况）。幂运算满足底数和指数都是实数。根据具体情况，底数和指数的数据类型和取值范围也各不相同，例如有的说是，底数是正整数，指数为非负数，有的问题中，底数为实数，指数是整数。

力扣中，幂运算相关的问题主要判断一个数是不是特定正整数的整数次幂，以及快速处理幂。

求2的次幂

参考题目介绍：231. 2 的幂 - 力扣（LeetCode）

在这里插入图片描述

本题目的解决思路还是很清晰的，我们可以用除的方法来逐步缩小n的值，另外一个就是使用位运算。

逐步缩小的方法就是：如果n是2的幂数，则 n > 0，且存在非负整数 k 是的 n = 2 ^ k。

首先判断 n 是否是正整数，如果 n 是 0 或者负整数，则 n 一定不是 2 的幂。

当 n 是整数时，为了判断 n 是否是 2 的幂，可以连续对 n 进行除以 2 的操作，直到 n 不能被 2 整除。此时如果 n = 1，那么 n 就是 2 的幂数，否则 n 不是 2 的幂。

代码如下：

    /**
     * 是否为2的幂
     * @param n
     * @return
     */
    public static boolean isPowerOfTwo(int n) {
        if ( n <= 0){
            return false;
        }
        while (n % 2 == 0){
            n /= 2;
        }
        return n == 1;
    }

当然这种方法效率不高，容易超时。（但是我们有法宝位运算加强🥰

如果采用位运算，该方法与我们之前说的统计数字转换二进制数以后1的个数思路一致。当 n > 0 时，考虑 n 的二进制表示。如果存在非负整数k 使得 n = 2 ^ k ，则n 的二进制表示为 1 后面跟着 k 个 0 。由此可以看出，正整数 n 是 2 的幂，当且仅当 n 的二进制表示中只有最高位是 1 ，其余位都是 0，此时满足 n & （ n - 1) = 0。此时代码就简单多了。

   public boolean isPowerOfTwo(int n) {
        return (n > 0) && (n &(n - 1)) == 0;
    }

注意：考虑优先级问题

求3的次幂

参考题目介绍：326. 3 的幂 - 力扣（LeetCode）

在这里插入图片描述

在这里插入图片描述
逐步缩小的方法对此也适用：

如果n是 3 的幂数，则 n > 0，且存在非负整数 k 是的 n = 3 ^ k。

首先判断 n 是否是正整数，如果 n 是 0 或者负整数，则 n 一定不是 3 的幂。

当 n 是整数时，为了判断 n 是否是 3 的幂，可以连续对 n 进行除以3 的操作，直到 n 不能被 2 整除。此时如果 n = 1，那么 n 就是 3 的幂数，否则 n 不是 3 的幂。

    public boolean isPowerOfThree(int n) {
        if(n <= 0){
            return false;
        }
        while(n % 3 == 0){
            n /= 3;
        }
        return n == 1;
    }

这个技巧和上面的一样，这里提供另一个思路：

由于输入 n 是 int 型，其最大值为 2 ^ 31 - 1。因此在int 型的数据范围内存在最大的 3 的幂，不会超过2 ^ 31 - 1，最大的 3 的幂是 3 ^ 19 = 1162261467。所以在 1 ~ 2 ^ 31 - 1内的数，如果是 3 的幂数，那么一点是1162261467的除数，所以这里就可以这样写：

    public boolean isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }

当然这个解法只是扩展思路的，没必要记住这个1162261467这个数字。

思考一下：这里换成4，5，6，7，8，9可以嘛？如果不可以，那如果只是针对素数3，5，7，11， 13 可以嘛？

求4的次幂

参考题目介绍：342. 4的幂 - 力扣（LeetCode）

在这里插入图片描述

在这里插入图片描述
上述同样的方法这里也可行，推荐换一种判断负数的方式

    public boolean isPowerOfFour(int n) {
        while(n != 0 && n % 4 == 0){
            n /= 4;
        }
        return n == 1;
    }

试想一下，这个题还能怎么优化，是否可以利用2的次幂呢？

这里留一个作业💕

当然除了幂运算，指数计算的思路与之类似，感兴趣也可以尝试下

50. Pow(x, n) - 力扣（LeetCode）

那这个题练练手

总结

提示：数组加法专题；字符串加法；二进制加法；幂运算；幂运算优化；

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ ("▔□▔)/

如有不理解的地方，欢迎你在评论区给我留言，我都会逐一回复 ~

也欢迎你关注我，喜欢交朋友，喜欢一起探讨问题。

在这里插入图片描述