题目描述

给你 nums ，它是一个大小为 2 * n 的正整数数组。你必须对这个数组执行 n 次操作。

在第 i 次操作时（操作编号从 1 开始），你需要：

选择两个元素 x 和 y 。
获得分数 i * gcd(x, y) 。
将 x 和 y 从 nums 中删除。
请你返回 n 次操作后你能获得的分数和最大为多少。

函数 gcd(x, y) 是 x 和 y 的最大公约数。

示例 1：

输入：nums = [1,2]
输出：1
解释：最优操作是：
(1 * gcd(1, 2)) = 1
示例 2：

输入：nums = [3,4,6,8]
输出：11
解释：最优操作是：
(1 * gcd(3, 6)) + (2 * gcd(4, 8)) = 3 + 8 = 11
示例 3：

输入：nums = [1,2,3,4,5,6]
输出：14
解释：最优操作是：
(1 * gcd(1, 5)) + (2 * gcd(2, 4)) + (3 * gcd(3, 6)) = 1 + 4 + 9 = 14

提示：

1 <= n <= 7
nums.length == 2 * n
1 <= nums[i] <= 106

求解思路

1. 这道题目是一道动态规划类型求解的题目，我们通过记忆化搜索+状态压缩来求解。
2. 最大公约数求解的模板代码就不多说了。
3. 核心思路:通过遍历模拟俩个位置的值，通过状态压缩的技巧来判断当前这俩个位置的元素是否被选中，如果没有，好的，更新当前位置的状态为1，否则跳过继续，最大值的更新过程需要我们根据题目的要求模拟即可。循环结束，将最大的值记录到缓存表中。

实现代码

class Solution {
    Map<Integer, Integer> map;

    public int maxScore(int[] nums) {
        map = new HashMap<>();
        return dfs(0, nums, 1);
    }

    public int dfs(int state, int[] nums, int index) {
        if (map.containsKey(state)) {
            return map.get(state);
        }
        int result = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i == j) continue;
                if ((state & (1 << i)) == 0 && (state & (1 << j)) == 0) {
                    int nowState = state;
                    nowState |= (1 << i);
                    nowState |= (1 << j);
                    result = Math.max(index * gcd(nums[i], nums[j]) + dfs(nowState, nums, index + 1), result);
                }
            }
        }
        map.put(state, result);
        return result;
    }

    public static int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }

}

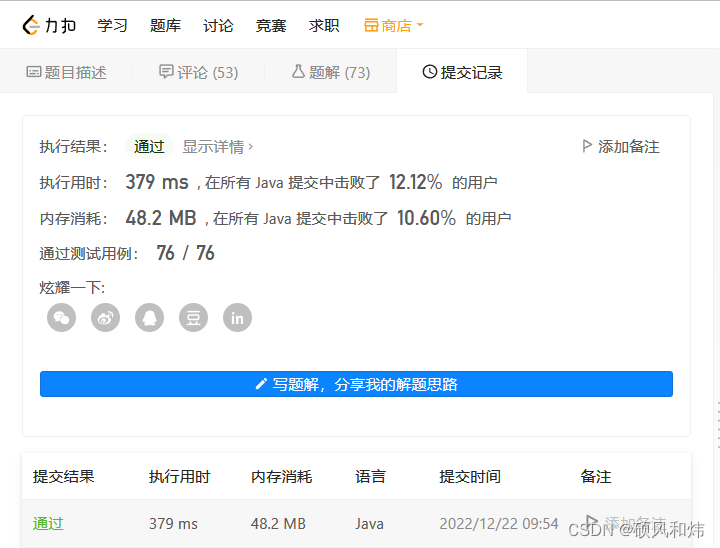
运行结果