深度搜索是一种计算机算法，用于在图或树等数据结构中查找目标节点。深度搜索从一个节点出发，依次遍历其所有子节点，直到找到目标节点或遍历完所有节点。如果找到目标节点，则搜索结束；如果遍历完所有节点仍未找到目标节点，则搜索失败。深度搜索通常使用递归实现，通过堆栈管理遍历的节点。深度搜索常用于解决迷宫、棋盘等问题，也是其他算法的核心组成部分，如搜索算法、动态规划等。 

模型：

void dfs(int step)

{

        判断边界

        for(int i=1;i<=n;i++)//尝试每种可能

             {

                  dfs(step+1)；//继续下一步

              }
         reutn；//返回
} 

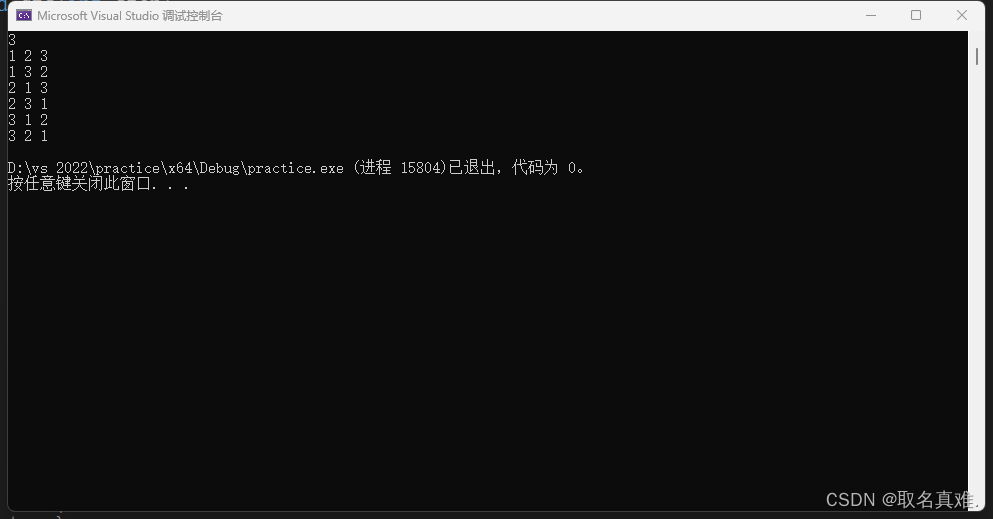
        深度优先搜索（DFS）全排列的基本思路是对于一个长度为n的数组，从第1个位置开始（即起始状态），对于每个未选择的数字，在当前的位置上进行一次选择，然后向下递归直到找到一个完整的排列，然后回溯到当前状态，再选择下一个未选择的数字进行搜索。 

#include<iostream>//深度优先搜索，全排列为例子
using namespace std;
int book[100];//标记
int n;
int a[100];
void dfs(int step)
{
	int i;
	if (step == n + 1)//判断边界
	{
		for (int i = 1; i <= n; i++)
			cout << a[i]<<" ";
		cout << endl;
		return;
	}
	for (int i = 1; i <= n; i++)//每种可能
	{
		if (book[i] == 0)
		{
			a[step] = i;
			book[i] = 1;
			dfs(step + 1);//继续下一步
			book[i] = 0;
		}
	}
	return;
}
int main()
{
	cin >> n;
	dfs(1);
}

       深度搜索算法可以用于解决迷宫问题。将迷宫抽象成一个矩阵，每个格子表示一个节点。将起点节点入栈，然后遍历其所有相邻节点。如果相邻节点是通路，则将其入栈，并在矩阵中标记为已访问。如果相邻节点是终点，则搜索结束；如果所有相邻节点都是墙，或者已经访问过，则回溯到上一步节点。重复以上步骤，直到遍历完所有节点或者找到终点。

#include<iostream>//深度优先搜索，迷宫最短路径问题
using namespace std;
int book[51][51];//标记是否走过
int n,m,q,p,x,y;
int a[51][51];
int min1 = 9999;
int next1[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };//右，下，左，上四个方向
void dfs(int x,int y,int step)
{
	int tx, ty;
	if (x == q && y == p)//走到终点
	{
		if (step < min1)
			min1 = step;
		return;
	}
	for (int k = 0; k < 4; k++)//向四个方向都走
	{
		tx = x + next1[k][0];
		ty = y + next1[k][1];
		if (tx<1 || tx>n || ty<1 || ty>m)
			continue;
		if (a[tx][ty] == 0 && book[tx][ty] == 0)//该条路不为障碍且没走过
		{
			book[tx][ty] = 1;//标记已走过
			dfs(tx, ty, step + 1);
			book[tx][ty] = 0;//尝试结束，取消标记
		}
	}
	return;
}
int main()
{
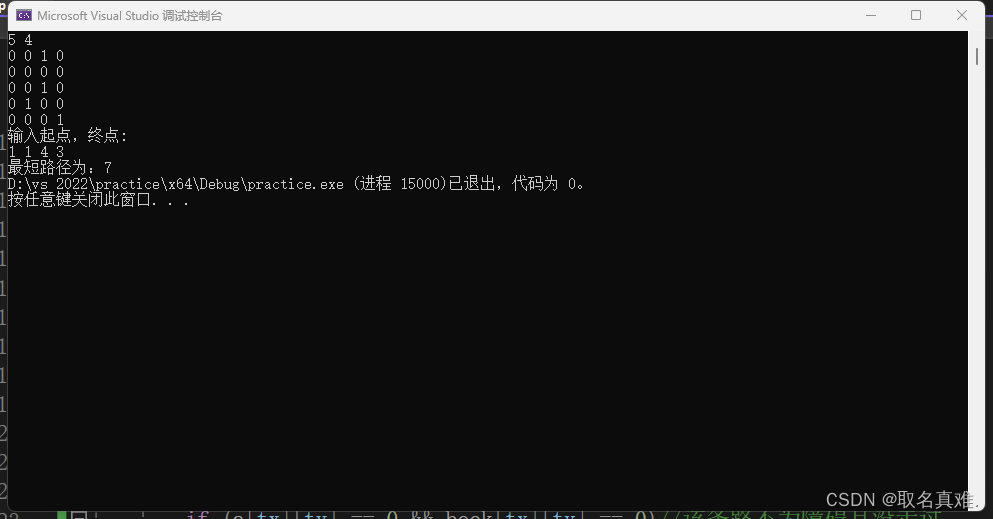
	cin >> n >> m;//迷宫规模
	for (int i = 1; i <= n; i++)//0为可走通路
		for (int j = 1; j <= m; j++)
			cin >> a[i][j];//输入迷宫
	cout << "输入起点，终点:" << endl;
	cin >> x >> y >> q >> p;//输入起点，终点
	book[x][y] = 1;//起点默认走过
	dfs(x,y,0);
	cout <<"最短路径为："<< min1;
}