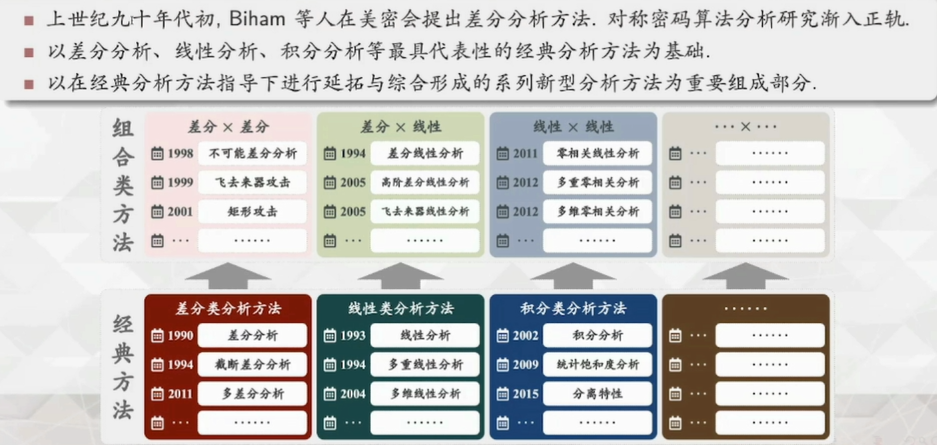
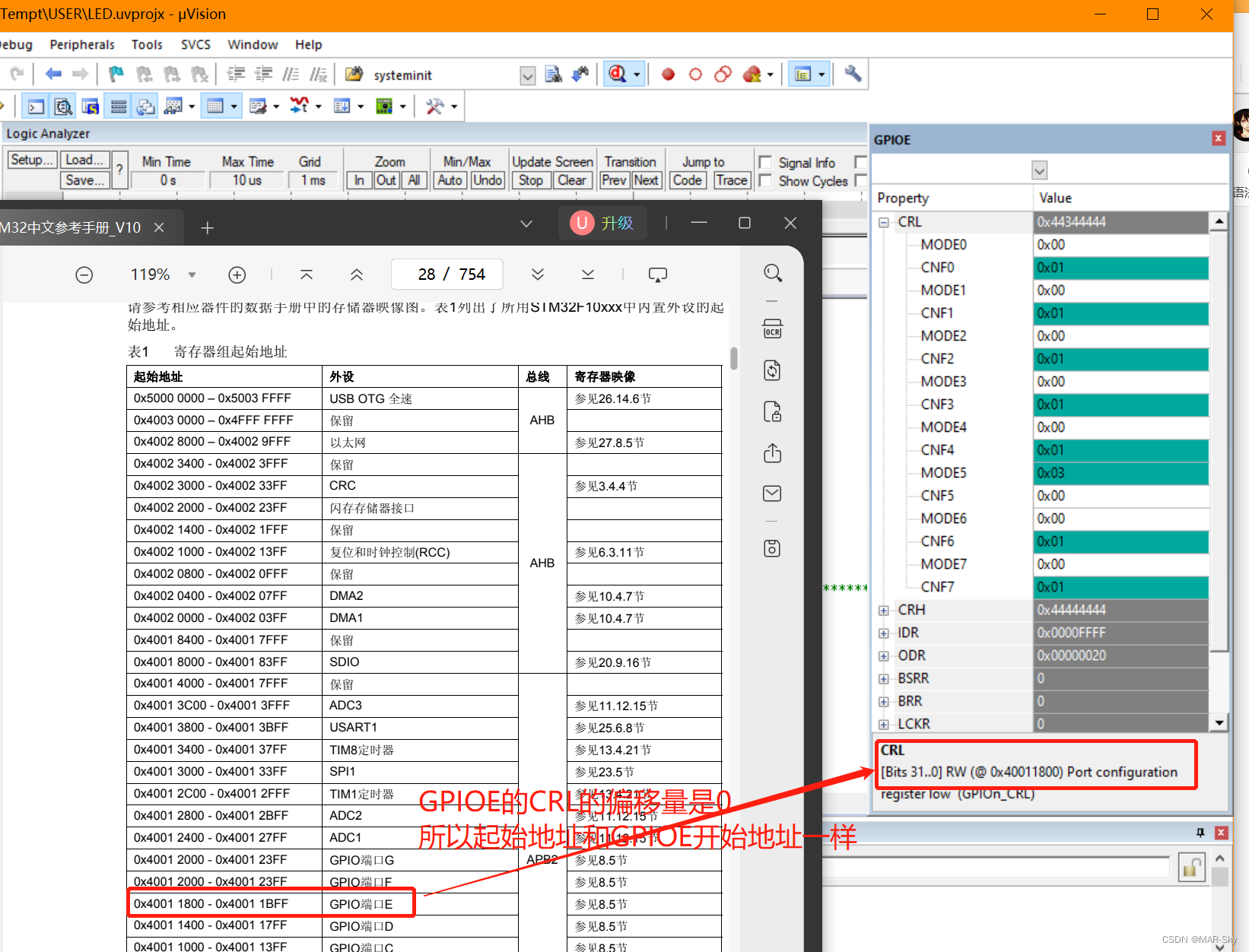
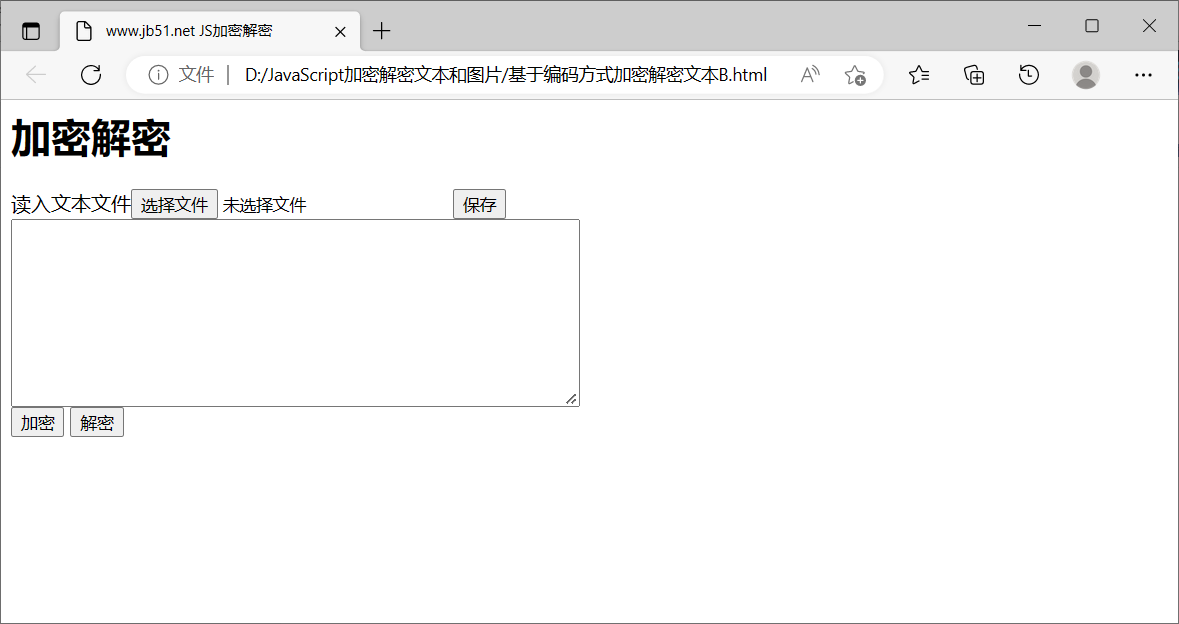
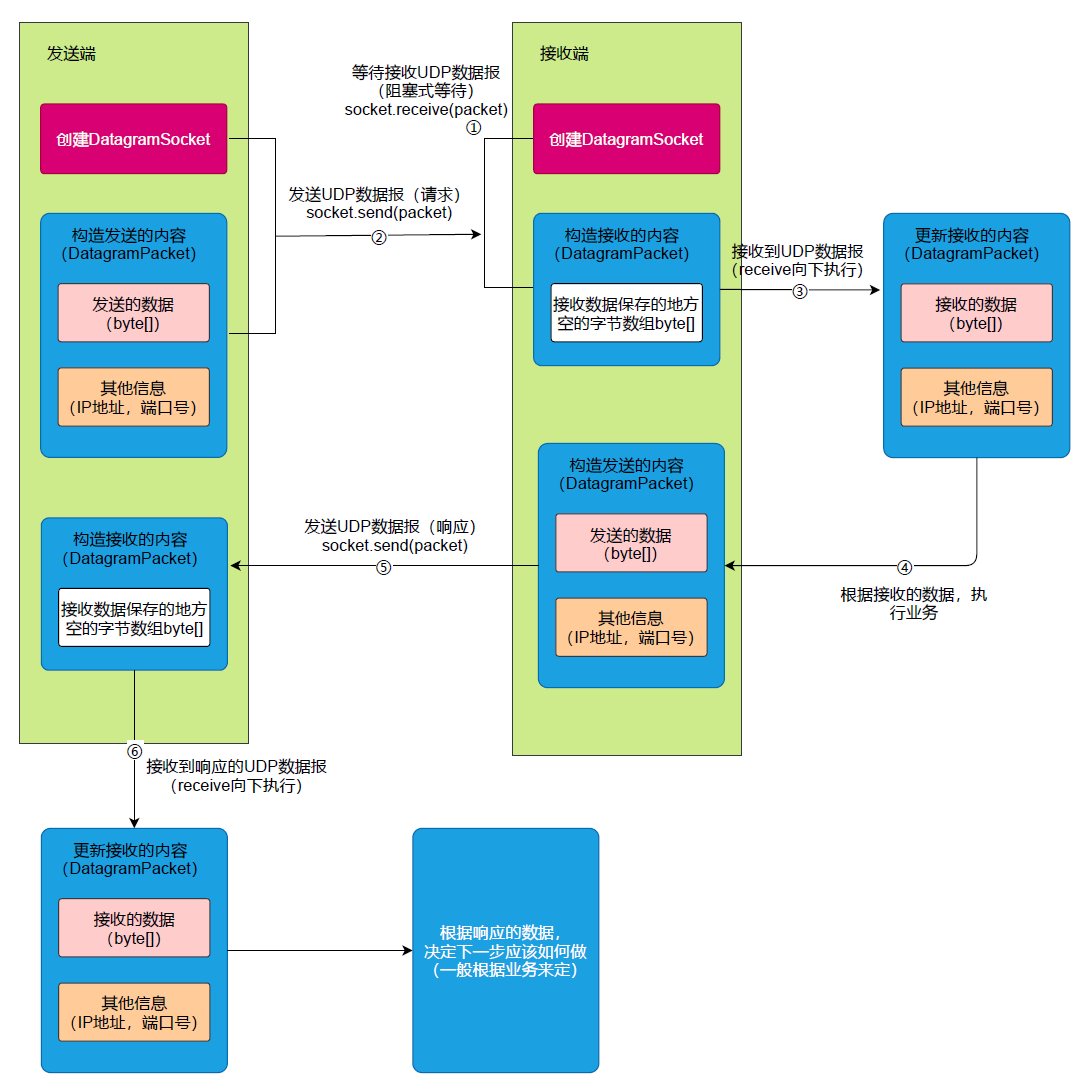
- 来自山大密码学讲座的PPT。
一些密码学领域常用名词术语
- Diffie-Hellman 密钥交换;Elgamal 加密和签名;DSA 签名;因相应的离散对数问题难解,大素数的原根可用于密钥交换;
- RSA加密和签名: 因大整数因子分解难算,合数可成公钥:
- 椭圆曲线密钥交换、加密和签名: 因其点群上离散对数问题难解,便有 Diffie-Hellman,Elgamal,DSA的圆曲线版本;
- 格密码:格中短向量难找,是合适的私钥选择;
- 密码学研究需要大量的大素数:素数定理保证每隔几百上千个数至少有一个素数,但需确定哪一个是,于是便有Robin-Miller算法和AKS算法。
- 密码学研究时常需要模素数的 (小) 原根: 实践上,可以从小的数试起,理论上得在广义黎曼假设下才能保证有不太大的原根存在。
- 椭圆曲线密码学应当选择具有素数个点的椭圆曲线: Schoof - Elkies - Atkin 算法(SEA) 使这样的任务在多项式时间完成。
- 在密码分析中我们需要较短的格向量: Lenstra-Lenstra-Lovasz 算法(LLL) 在很多情况下有满意的表现。
- 计算模幂和标量乘: 分治思想下的平方-乘积方法很好地满足当前的实际需求。
- 计算模逆: 秦九韶的大衍求一术是一个高效且优美的方法
- 快速的大数乘法或多项式乘法: 快速傅里叶变换是个强有力的工具;



密码学研究和密码学发展脉络
- 密码学研究层次

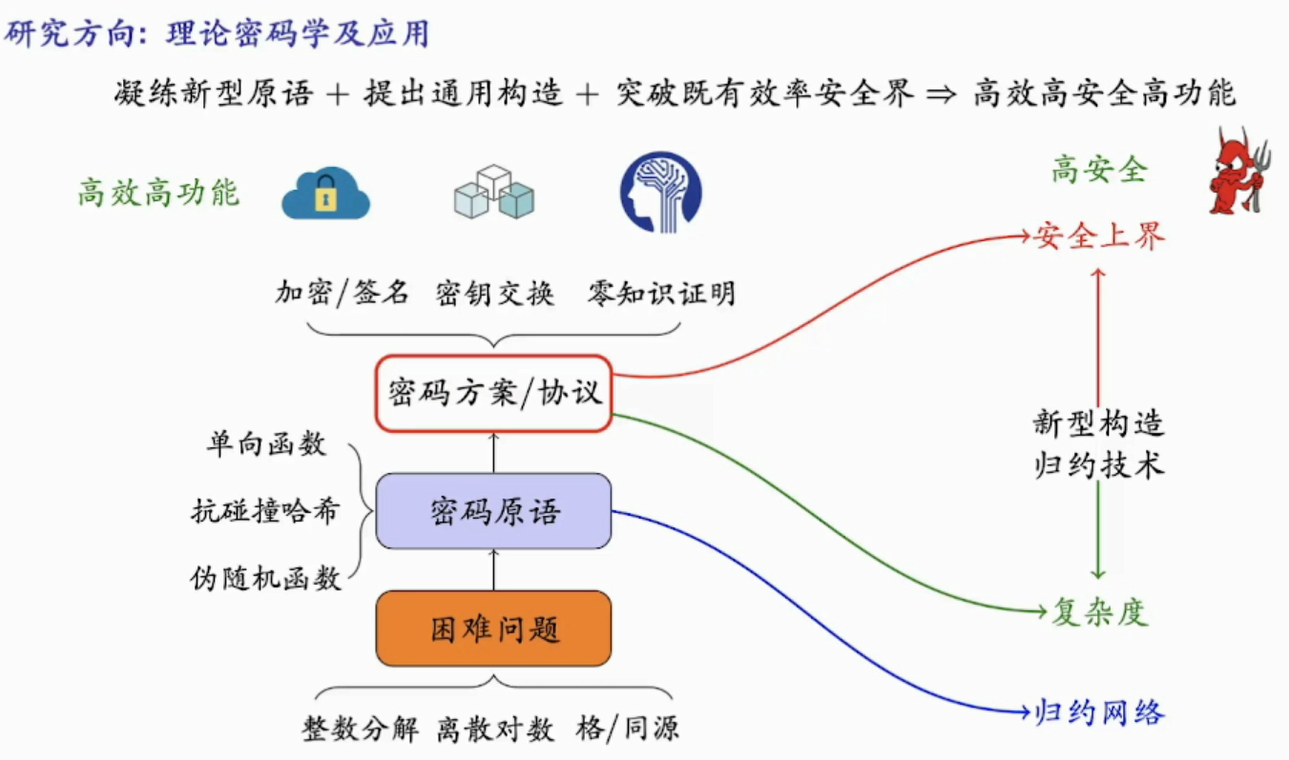
- 密码原语
- 归约技术、归约网络
- 数据隐私保护的三个时代

- 数据隐私保护的环节

- 数据隐私保护方案

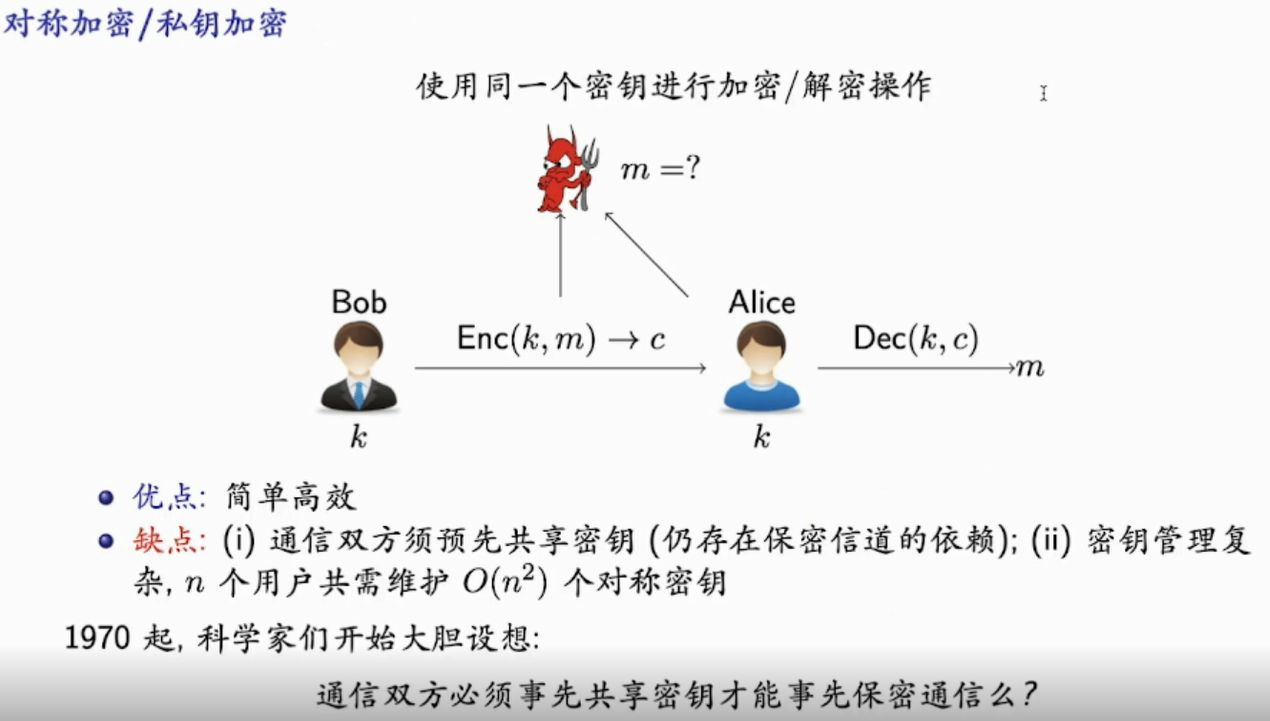




- 单向性安全
- 可证明安全
- 语义安全
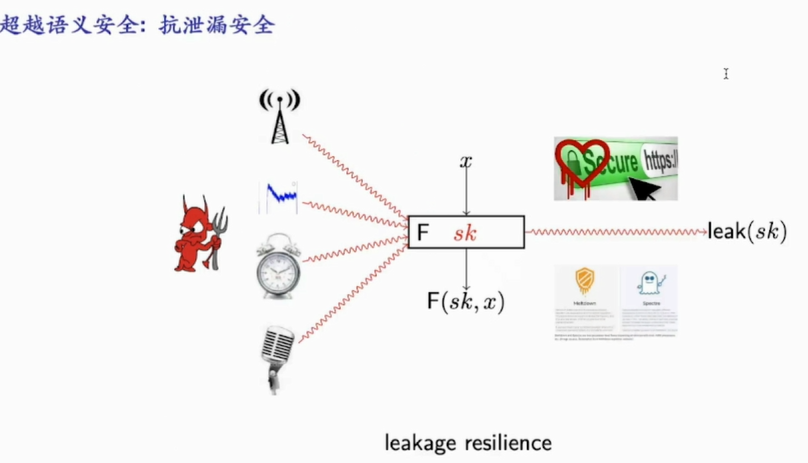
- 抗泄露安全


隐私计算

高功能加密

- 外包计算

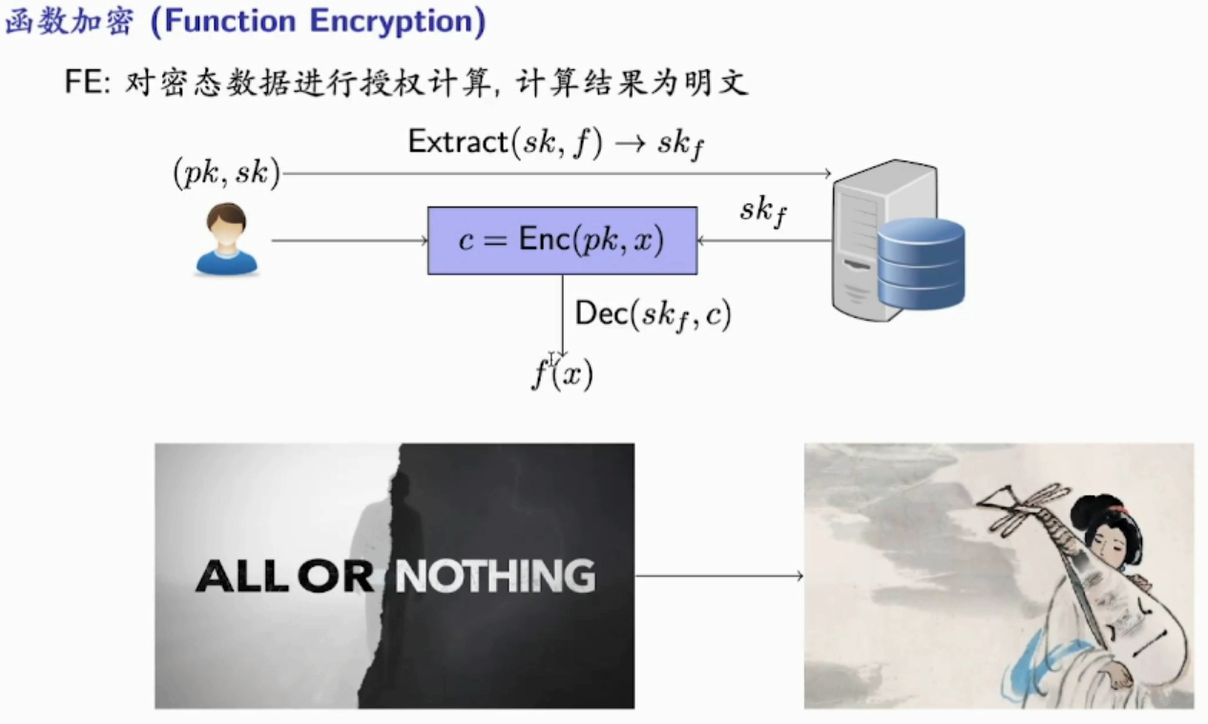
(PPT中有错字,输出y) - 函数加密 Function Encryption



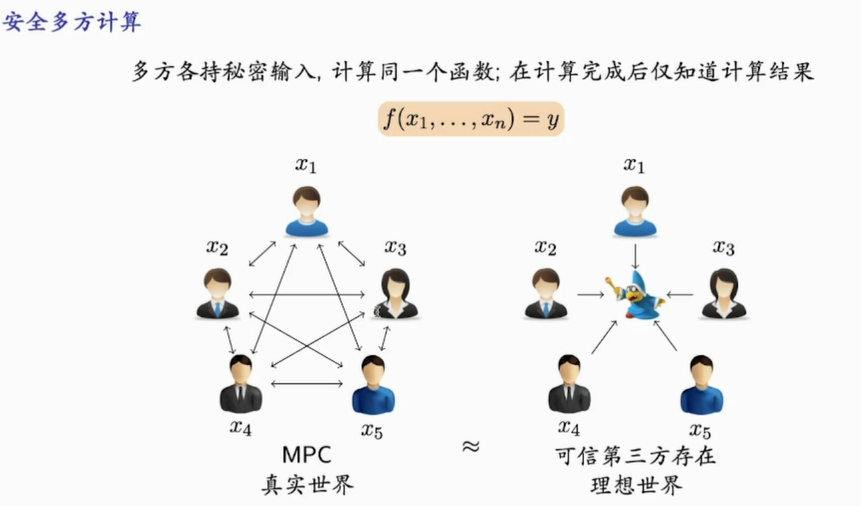
安全多方计算



零知识证明






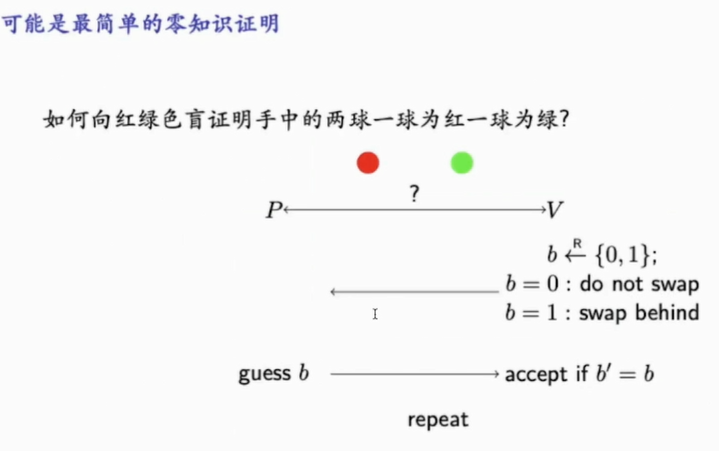




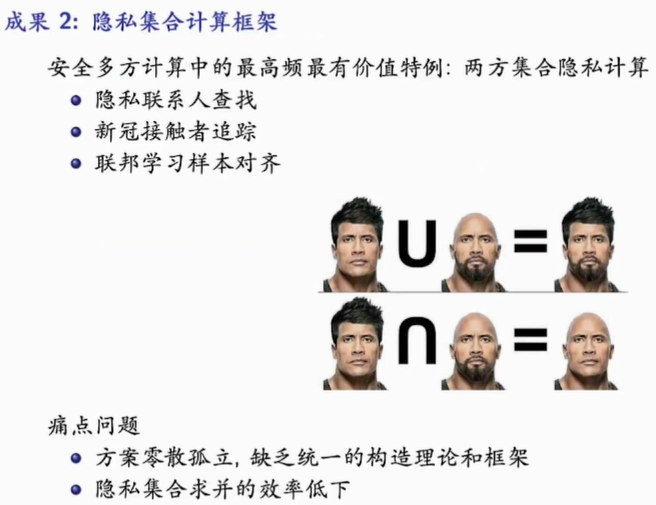
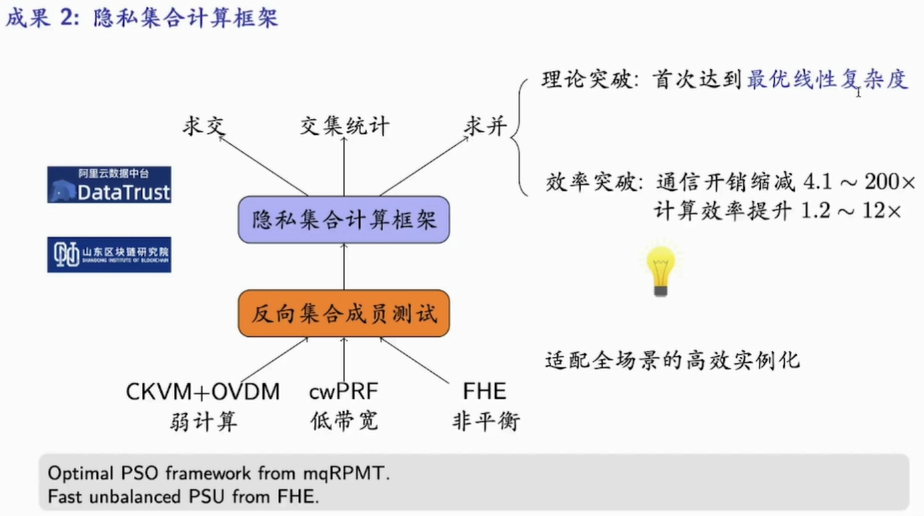
密码工程








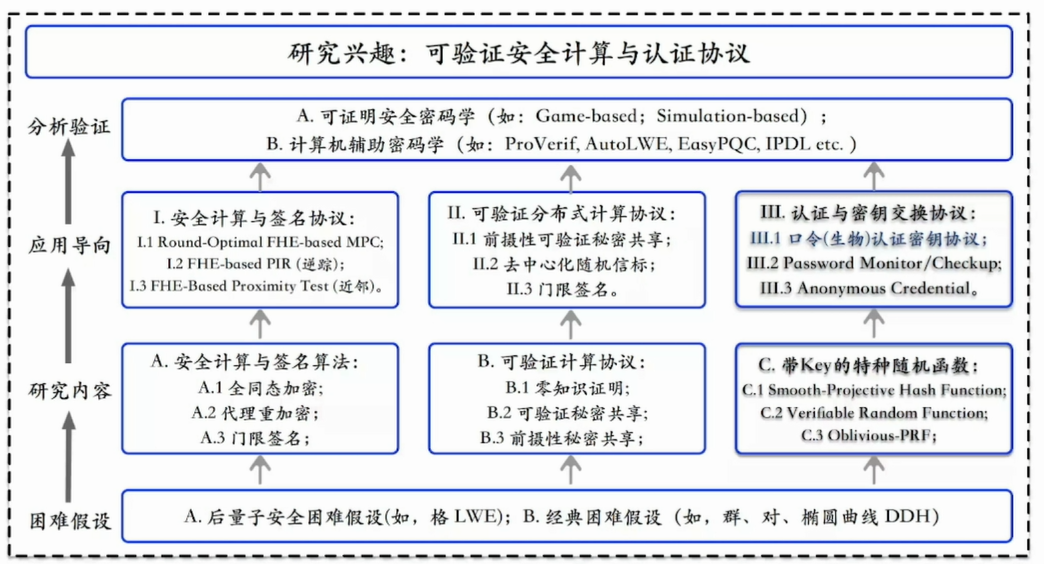
密码分析