题目描述

看本文需要准备的知识
1.最长上升子序列(lis)的算法思想和算法模板
2.acwing1010拦截导弹(lis+贪心)题解 本题题解,需要知道这种贪心算法
3.简单了解dfs暴力搜索、剪枝、搜索树等概念
思路讲解
dfs求最小步数有两种方法:记一个全局最小值,迭代加深
bfs的缺点:空间太大、不好剪枝
此处采用dfs的迭代加深
首先,这道题的爆搜思路为:从前往后枚举每颗导弹属于某个上升子序列,还是下降子序列;
如果属于上升子序列,则枚举属于哪个上升子序列(包括新开一个上升子序列);如果属于下降子序列,可以类似处理
那么搜索树就会十分的大,如下所示:
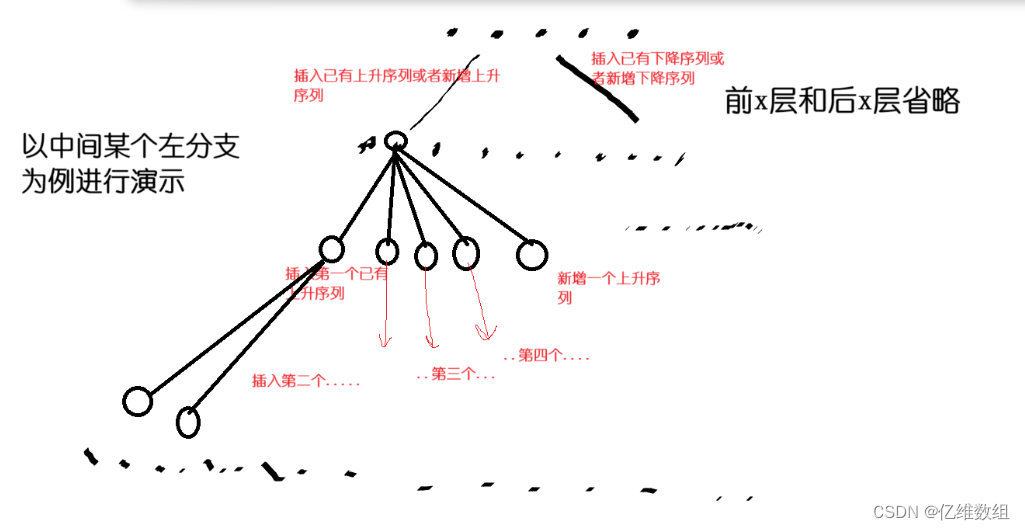
如何剪枝,首先可以采用acwing1010的贪心策略(下面放题解链接),这样就不用遍历插入每一个序列的分支了,而是在上升时(包含插入已有上升序列和新增一个上升序列)或者下降时(包含插入已有下降序列和新增一个下降序列)就确定了要选择哪种分支,而把其它分支全部剪掉!
acwing1010拦截导弹(lis+贪心)题解
优化之后,搜索树就简化为:
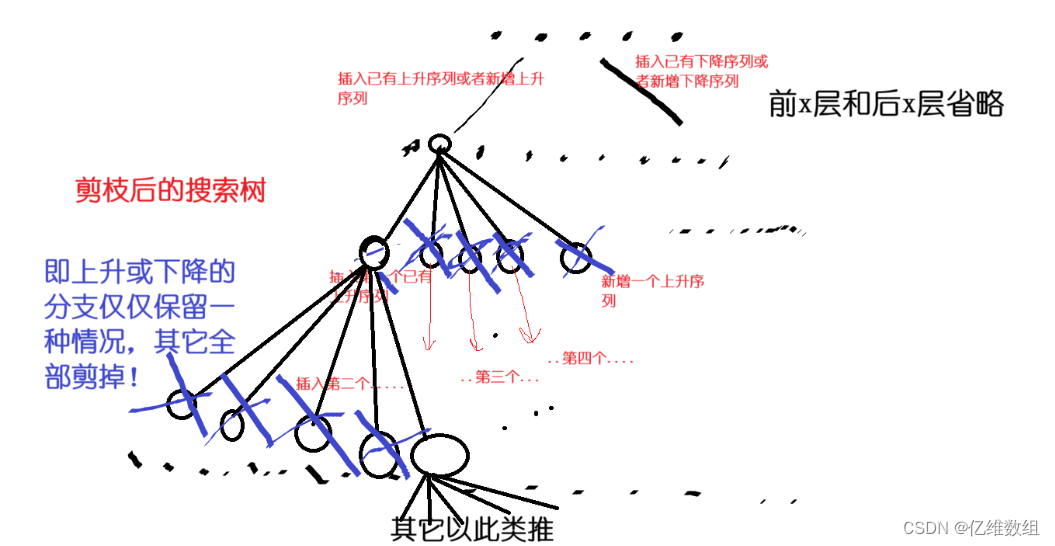 dfs的函数原型设为:
dfs的函数原型设为:
dfs(u,su,sd):
其中u代表现在遍历的序列第几个数,su表示现在上升序列的个数,sd表示现在下降序列的个数
答案res初始化为n(因为最多需要的防御系统的个数就是n)
在dfs的开头也可以做一个小剪枝:
if(su+sd>=res)return;意思是:如果此次dfs的su+sd大于等于当前已经算出的需要最少的防御系统数量,就直接把这个分支剪掉,因为在这之后su+sd不可能比res小,就不可能在这以下的分支获得更小的res
完整代码
#include<iostream>
using namespace std;
const int N=55;
int res;
int h[N],up[N],down[N];
int n;
void dfs(int u,int su,int sd)
{
if(su+sd>=res)return;
if(u==n)
{
res=su+sd;
return;
}
int k=0;
while(k<su&&up[k]>h[u])k++;
if(k<su)
{
int t=up[k];
up[k]=h[u];
dfs(u+1,su,sd);
up[k]=t;
}
else
{
up[k]=h[u];
dfs(u+1,su+1,sd);
}
k=0;
while(k<sd&&down[k]<h[u])k++;
if(k<sd)
{
int t=down[k];
down[k]=h[u];
dfs(u+1,su,sd);
down[k]=t;
}
else
{
down[k]=h[u];
dfs(u+1,su,sd+1);
}
}
int main()
{
while(cin>>n,n)
{
for(int i=0;i<n;i++)cin>>h[i];
res=n;
dfs(0,0,0);
cout<<res<<endl;
}
return 0;
}

![2023年中国智慧医院市场现状及行业发展趋势分析[图]](https://img-blog.csdnimg.cn/img_convert/d5dec0e1b777be6ad6d4376d5d9a09c7.png)
![2023年中国连锁麻辣烫市场发展趋势分析:连锁麻辣烫行业规模将持续增长[图]](https://img-blog.csdnimg.cn/img_convert/47bafa59a252afec69d42a5201174bb1.png)
![2023年中国香樟木家具行业分析:定制化和个性化的需求不断增加[图]](https://img-blog.csdnimg.cn/img_convert/ce9af28a880f7e8a0c0070e75c5d2a3b.png)