哈希集合

请读者思考，num拆分成num1和num2，要使得num1 + num2最小，应满足两条性质：

1. num1和num2位数相同，或最多差一位。
2. num1和num2应按数值从小到大在num中取数。

想到统计num的位数，以实现性质1的需要；想到用哈希集合a[10]，统计数字{0~9}在num中出现的次数，以实现性质2的需要。

请看更具体的性质：

1. num是奇数时，num1和num2最多差一位；num是偶数时，num1和num2位数相同。
2. num1先取一个数，num2再取一个数，取数时按数值从小到大在num中取数。

请看下列代码：

class Solution {
public:
    int splitNum(int num) {
        int a[10] = { 0 };
        int count = 0;
        int num1  = 0, num2 = 0;
        while (num) {
            count ++;
            a[num % 10] ++;
            num /= 10;
        }
        if (count & 1) { // 奇数
            count --;
            for (int i = 0; i < 10; i ++) {
                if (a[i]) {
                    a[i] --;
                    num1 += i;
                    break;
                }
            }
        } 
        while (count) {
            for (int i = 0; i < 10; i ++) {
                if (a[i]) {
                    num1 *= 10;
                    num1 += i;
                    a[i] --;
                    count --;
                    break;
                }
            }
            for (int i = 0; i < 10; i ++) {
                if (a[i]) {
                    num2 *= 10;
                    num2 += i;
                    a[i] --;
                    count --;
                    break;
                }
            }
        }
        return num1 + num2;
    }
};

更具体的，我们发现奇数无需区分，请看推理：
设num是奇数，num1多取了一位数(比num2多一位)。不考虑num1的首位，num1的后续排列只有两种(交替取数)，且num1的排列刚好和num2的排列相反。因此{num1的排列} + {num2的排列}是一个定值(按性质1/2交替取数的前提下！！)，所以奇偶数无需区分。

class Solution {
public:
    int splitNum(int num) {
        int a[10] = { 0 };
        int count = 0;
        int num1  = 0, num2 = 0;
        while (num) {
            count ++;
            a[num % 10] ++;
            num /= 10;
        }
        while (count) {
            for (int i = 0; i < 10; i ++) {
                if (a[i]) {
                    num1 *= 10;
                    num1 += i;
                    a[i] --;
                    count --;
                    break;
                }
            }
            for (int i = 0; i < 10; i ++) {
                if (a[i]) {
                    num2 *= 10;
                    num2 += i;
                    a[i] --;
                    count --;
                    break;
                }
            }
        }
        return num1 + num2;
    }
};

时间复杂度 $O(logn)$ : $n$ 是数字大小，按数位处理数字的时间复杂度$O(lo{g}_{10}n)$ 。忽略常数，时间复杂度 $O(logn)$ 。
空间复杂度 $O(|C|)$ : 哈希集合的大小 $|C|$，空间复杂度 $O(|C|)$ 。

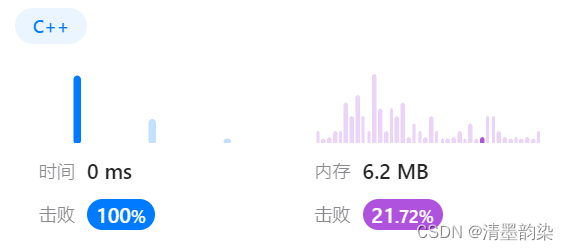
AC

致语

• 理解思路很重要
• 读者有问题请留言，清墨看到就会回复的。