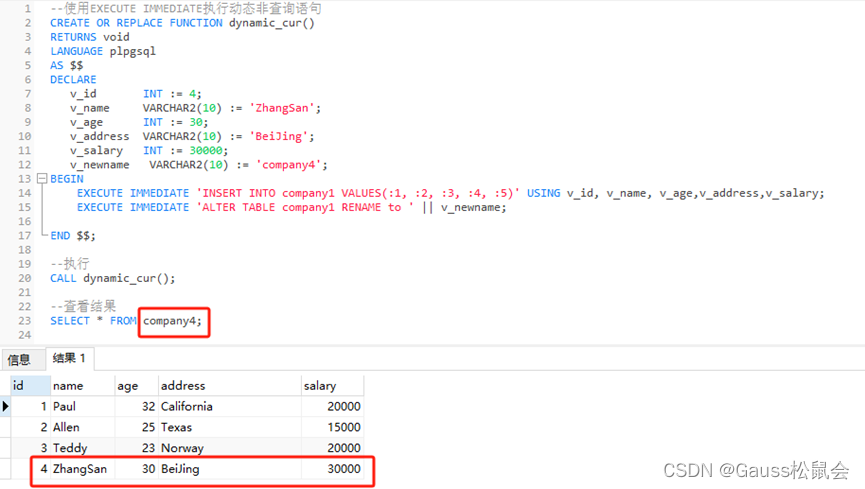
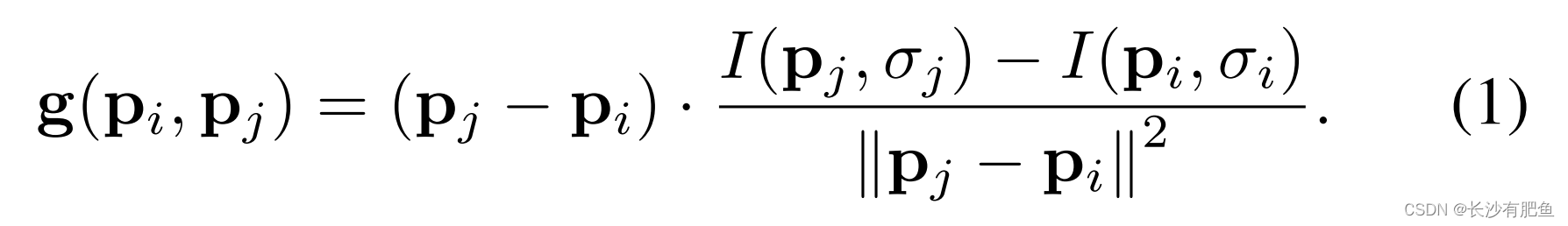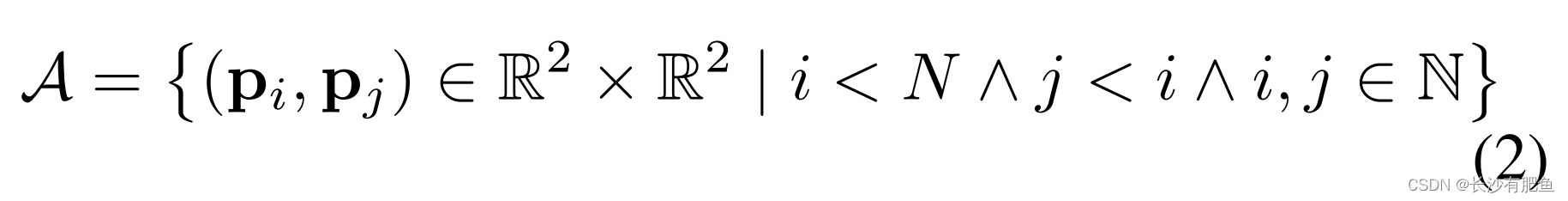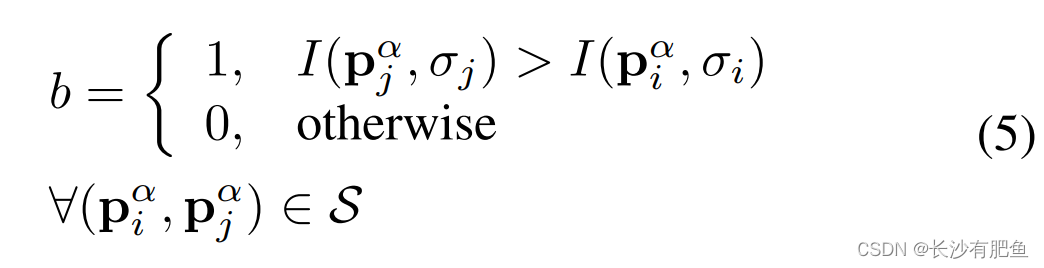pdf链接：https://pan.baidu.com/s/1gFAYMPJStl4cF0CswY9cMQ 
提取码：yyds

摘要

从图像中有效和高效地生成关键点是文献中深入研究的问题，并形成了许多计算机视觉应用的基础。该领域的领导者是SIFT和SURF算法，它们在各种图像转换下表现出出色的性能，其中SURF算法被认为是迄今为止高性能方法中计算效率最高的。

本文提出了一种用于关键点检测、描述和匹配的新方法BRISK。对基准数据集的全面评估显示，尽管计算成本大大降低(在某些情况下比SURF快一个数量级)，但BRISK在最先进的算法中具有自适应的高质量性能。提高速度的关键在于应用了一种新型的基于尺度空间FAST的检测器，并结合了从每个关键点邻域的专用采样检索的强度比较中提取的位串描述符。

1 介绍

将图像分解为感兴趣的局部区域或“特征”是计算机视觉中广泛应用的技术，用于在利用局部外观属性的同时降低复杂性。图像表示、物体识别和匹配、3D场景重建和运动跟踪都依赖于图像中稳定的、有代表性的特征，这推动了研究，并产生了大量解决这一问题的方法。

理想的关键点检测器发现突出的图像区域，即使改变视点也能重复检测;更一般地说，它对所有可能的图像变换都具有鲁棒性。类似地，理想的关键点描述符捕获包含在检测到的显著区域中的最重要和最独特的信息内容，以便在遇到相同的结构时可以识别出来。此外，除了满足这些属性以实现所需的关键点质量外，还需要优化检测和描述的速度，以使其适应当前任务的时间限制。

原则上，最先进的算法针对的是对计算精度或速度有严格要求的应用。Lowe的SIFT方法[9]被广泛接受为目前可用的最高质量的选项之一，有望对各种常见的图像转换具有独特性和不变性-然而，以计算成本为代价。在频谱的另一端，FAST[14]关键点检测器和BRIEF[4]描述方法的组合为实时应用程序提供了更合适的替代方案。然而，尽管在速度上有明显的优势，后一种方法在可靠性和鲁棒性方面受到影响，因为它对图像扭曲和转换的容忍度最低，特别是对平面内旋转和尺度变化。因此，像SLAM[6]这样的实时应用需要使用概率方法[5]进行数据关联，以发现匹配共识。

从图像中提取合适特征的内在困难在于平衡两个相互竞争的目标:高质量的描述和低计算需求。这就是这项工作旨在用BRISK方法设定一个新的里程碑的地方。也许解决这个问题最相关的工作是SURF[2]，它已被证明具有鲁棒性和速度，只有，正如我们的结果所示，BRISK在更少的计算时间内实现了类似的匹配质量。简而言之，本文提出了一种从图像中生成关键点的新方法，其结构如下:

•尺度空间关键点检测:使用显著性准则在图像和尺度维度上识别感兴趣的点。为了提高计算效率，在图像金字塔的八度层和中间的层中检测关键点。通过二次函数拟合得到连续域内各关键点的位置和尺度。

•关键点描述:在每个关键点的邻域采用由分布在适当缩放的同心圆上的点组成的采样模式来检索灰度值:处理局部强度梯度，确定特征特征方向。最后，利用定向的BRISK采样模式获得成对亮度比较结果，并将其组合到二进制的BRISK描述子。

生成后，由于描述符的二进制性质，可以非常高效地匹配BRISK关键点。BRISK着重于计算效率，还利用了当今架构广泛支持的SSE指令集带来的速度优势。

2 相关工作

在文献中可以找到大量关于识别局部兴趣点用于图像匹配的描述，其中哈里斯和斯蒂芬斯[7]提出了最早的而且可能是最著名的角点检测。Mikolajzyk等人的开创性工作[13]对当时最有能力的检测方法进行了全面评估，发现没有单一的通用检测器，而是根据应用的背景揭示了不同方法的互补特性。在具有严格实时约束的最新方法中，近期的用于关键点检测的FAST准则[14]已变得越来越流行，而AGAST[10]扩展了这项工作以提高性能。

SIFT[9]是目前文献中质量最高的特征提取方法之一。对照明和视点变化的高描述能力和鲁棒性使SIFT描述符在[11]的调查中排名最高。然而，此描述符的高维度使SIFT变得异常缓慢。PCA-SIFT[8]将描述符从128维减少到36维，但是损害了它的独特性并增加了描述符形成的时间，这几乎抵消了匹配速度的提高。GLOH描述符[12]在这里也值得注意，因为它属于类SIFT家族，并且已被证明比SIFT更独特，但计算成本也更高。

对高质量，高速功能的需求不断增长，导致人们对能够以更高速率处理更丰富数据的算法进行了更多研究。值得注意的是Agrawal等人的工作[1]。他们采用中心对称的局部二进制模式替代SIFT的方向直方图方法。最新的Brief[4]专为超快速描述和匹配而设计，由二进制字符串组成，其中包含在随机预定像素位置进行简单图像强度比较的结果。尽管此方法简单有效，但该方法对图像旋转和缩放比例非常敏感，从而限制了其在一般任务中的应用。

目前最吸引人的算法可能是SURF[2]，它已被证明比SIFT快得多。SURF检测使用Hessian矩阵的行列式(blob检测器)，而描述是通过对感兴趣区域的Haar小波响应求和来完成的。在最新技术方面，SURF展示了令人印象深刻的时间表现，然而在速度方面，与目前可用的最快但质量有限的功能相比仍相差几个数量级。

在本文中，我们提出了一种称为“BRISK”的新颖方法，用于高质量、快速的关键点检测、描述和匹配。顾名思义，该方法在很大的程度上是旋转以及尺度不变的，可实现与最新技术相当的性能，同时显著降低了计算成本。在对该方法进行描述之后，我们介绍了在基准数据集上执行的实验结果，并使用了标准的评估方法[12，13]，即提出了关于SURF和SIFT的BRISK评估，它们被普遍认为是常见图像变换下的比较标准。

3  BRISK方法

在本节中，我们将以读者可以理解和复现的细节级别描述BRISK的关键阶段，即特征检测、描述符组成以及关键点匹配。重要的是要注意，该方法的模块化允许将BRISK检测器与任何其他关键点描述符结合使用，反之亦然，可以针对所需的性能和手头的任务进行优化。

3.1.尺度空间关键点检测

着重于计算效率，我们的检测方法受到Mair等人[10]的工作启发，用于检测图像中感兴趣的区域。他们的AGAST本质上是对现在流行的FAST的加速性能的扩展，事实证明，FAST是特征提取的非常有效的基础。为了实现对高质量关键点至关重要的尺度不变性，我们不仅通过在图像平面中搜索最大值，而且还使用FAST评分作为衡量显著性的尺度在尺度空间中搜索最大值，从而更进一步。尽管以比其他高性能检测器(例如Fast-Hessian[2])更粗的间隔离散化尺度轴，但BRISK检测器仍估算连续尺度空间中每个关键点的真实比例。

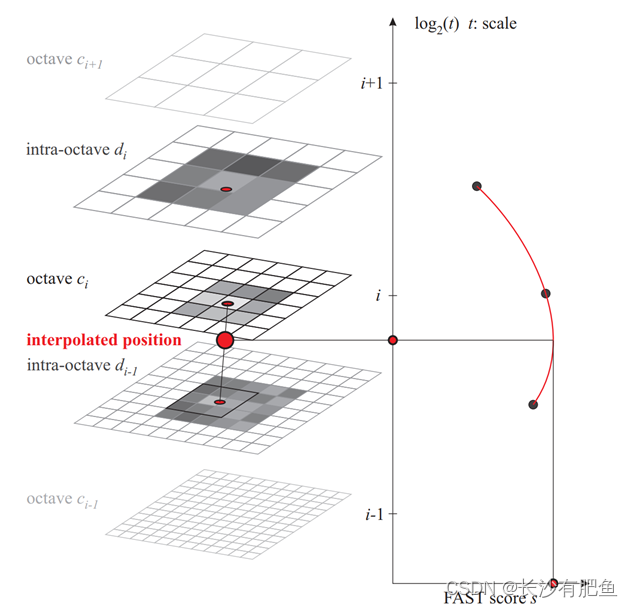
在BRISK框架中，尺度空间金字塔层由n个八度ci和n个内部八度di组成，其中i = {0，1，…，n−1}，通常n=4。通过对原始图像进行半采样（对应于c0）来形成八度。每个八度di都位于ci和ci+1层之间（如图1所示）。通过将原始图像c0下采样1.5倍来获得第一个八度d0，而其余的八度层则通过连续的半采样得出。因此，如果t表示尺度，则t(ci)=2i且t(di) = 2i·1.5。

图1.尺度空间兴趣点检测:通过分析ci中相邻的8个显著性分数以及相邻上下层中对应的分数斑块，在ci八度di处识别出一个关键点(即显著性最大值)。在所有三个感兴趣的层中，局部显著性最大值在沿刻度轴拟合1D抛物线之前被亚像素细化，以确定关键点的真实刻度。然后，关键点的位置也在最接近确定尺度的补丁最大值之间重新插值。

这里需要注意的是，FAST和AGAST都为关键点检测提供了不同的掩膜形状替代方案。在BRISK中，我们主要使用9-16掩膜，这实际上要求16像素圆中至少9个连续的像素要比中心像素足够亮或更暗才能满足FAST标准。

最初，FAST 9-16检测器分别应用于每个八度和八度内，使用相同的阈值T来识别潜在的感兴趣区域。接下来，在尺度空间中对属于这些区域的点进行非极大值抑制:首先，所讨论的点需要相对于同一层中相邻的8个FAST分数s满足最大条件。分数定义为最大阈值，仍然考虑图像点的一个角落。其次，上面一层和下面一层的分数也需要低一些。我们检查内部相同大小的正方形补丁:边长被选择为2像素的层与怀疑的最大。由于相邻层(因此其FAST分数)是用不同的离散化表示的，因此在补丁的边界处应用了一些插值。图1描述了这种抽样和极大值搜索的示例。

在八度程c0处跨刻度轴的极大值检测是一种特殊情况:为了获得c0以下虚拟八度程d−1的FAST分数，我们对c0应用FAST 5-8掩码。但是，在d−1的patch中的分数在这种情况下不需要低于c0八度的被测点的分数。

考虑到图像显著性是一个连续的量，不仅跨越图像，而且沿着尺度维度，我们对每个检测到的最大值执行亚像素和连续尺度细化。为了限制细化过程的复杂性，我们首先将最小二乘意义上的二维二次函数拟合到三个分数斑块(分别在关键点层、上面一层和下面一层中获得)，从而得到三个亚像素细化的显著性最大值。为了避免重采样，我们在每一层上考虑一个3 × 3的评分补丁。接下来，这些细化的分数被用来拟合沿着刻度轴的一维抛物线，产生最终的分数估计和刻度估计的最大值。作为最后一步，我们在确定的尺度旁边的层中的补丁之间重新插值图像坐标。在Boat序列的两张图像中(在第4节中定义)进行BRISK检测的示例如图2所示。

图2.船序列图像1和2上的一个BRISK检测示例的特写，显示小缩放和面内旋转。圆圈的大小表示检测到的关键点的比例，而径向表示它们的方向。为了清晰起见，这里的检测阈值设置为比典型设置更严格的值，可重复性略低。

3.2.关键点描述

给定一组关键点(由亚像素细化图像位置和相关的浮点比例值组成)，通过连接简单亮度比较测试的结果，将BRISK描述符组成为二进制字符串。这个想法在[4]中已经被证明是非常有效的，但是在这里我们以一种更定性的方式使用它。在BRISK中，我们识别每个关键点的特征方向，以允许方向规范化描述符，从而实现旋转不变性，这是一般鲁棒性的关键。此外，我们仔细选择亮度比较，重点是最大限度地提高描述性。

3.2.1  采样模式和旋转估计

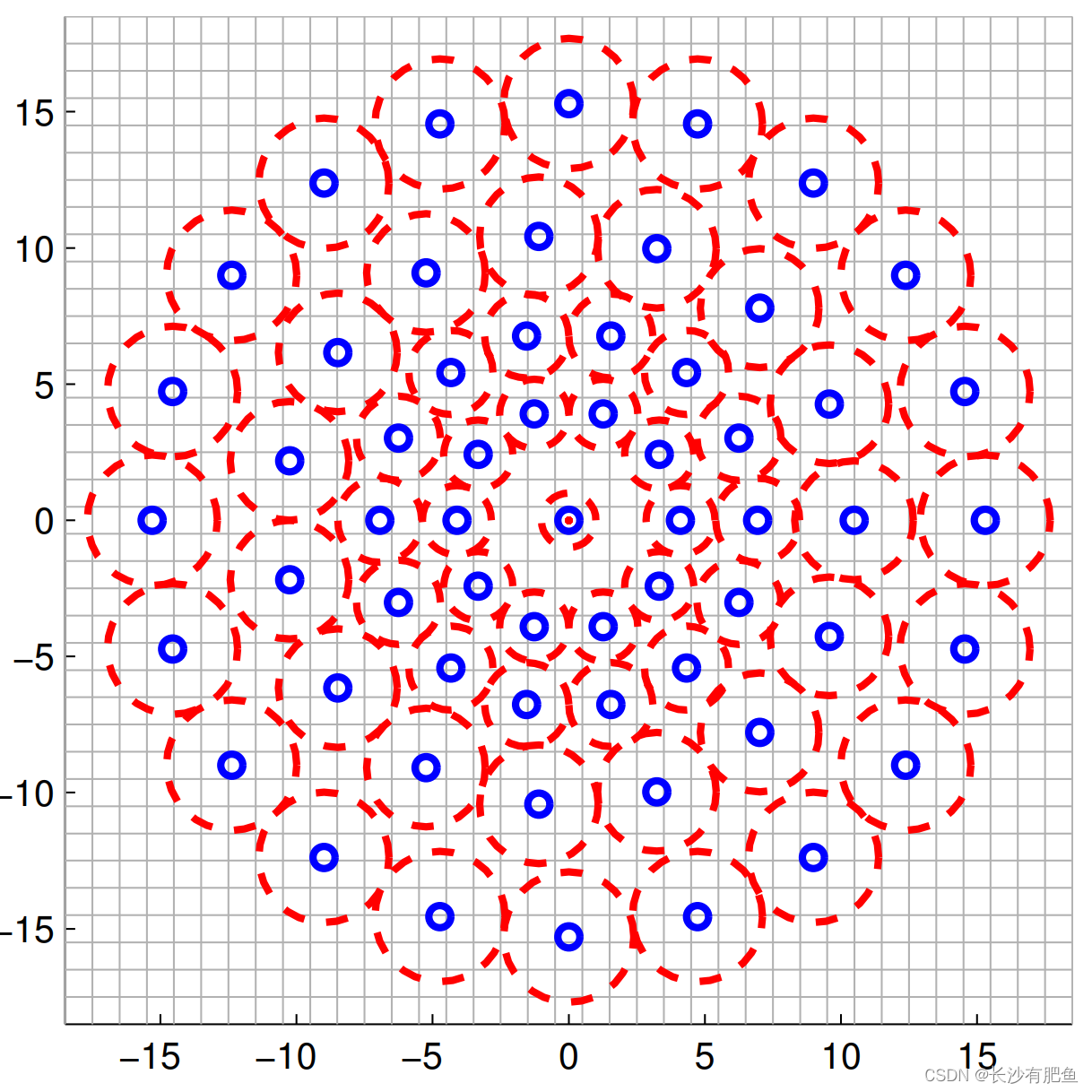
BRISK描述符的关键概念是利用一种模式对关键点的邻域进行采样。如图3所示，该模式在与关键点同心圆上定义了N个等距的位置。虽然此模式类似于DAISY描述符[15]，但需要注意的是，它在BRISK中的使用完全不同，因为DAISY是专门为密集匹配构建的，故意捕获更多信息，从而导致对速度和存储的要求很高。

图3.N = 60点的BRISK抽样模式:蓝色小圆圈表示抽样位置;较大的红色虚线圆以半径σ绘制，对应于用于平滑采样点上强度值的高斯核的标准差。所示模式适用于t = 1的比例。

为了避免在对图案中点pi的图像强度采样时产生混叠效应，我们采用了高斯平滑，标准差σi与各自圆上点之间的距离成正比。对图像中特定关键点k进行相应的定位和缩放，让我们考虑N·(N−1)/2个采样点对中的一个(pi,pj)。利用这些点的平滑强度值I(pi,σi)和I(pj,σj)来估计局部梯度g(pi,pj):

考虑所有采样点对的集合A：

我们定义一个短距离配对的子集S和长距离配对的另一个子集L：

    阈值距离设置为δmax = 9.75t， δmin = 13.67t (t为k的刻度)，通过L中的点对迭代，我们估计关键点k的整体特征模式方向为:

长距离对用于此计算，基于局部梯度相互湮灭的假设，因此在全局梯度确定中不是必需的-这也通过距离阈值δmin的变化实验得到了证实。

3.2.2构建描述符

为了形成旋转和尺度归一化描述符，BRISK在关键点k周围应用旋转α = arctan2(gy, gx)的采样模式。位向量描述符dk是通过执行点对(即在旋转模式中)的所有短距离强度比较来组装的，这样每个位b对应于:

虽然BRIEF描述符也是通过亮度比较组成的，但除了明显的采样模式的预缩放和预旋转之外，BRISK还有一些基本的区别。首先，BRISK采用确定性采样模式，在关键点周围的给定半径内产生均匀的采样点密度。因此，量身定制的高斯平滑将不会通过模糊比较中的两个接近的采样点而意外扭曲亮度比较的信息内容。此外，与成对比较相比，BRISK使用的采样点大大减少(即单个点参与更多的比较)，从而限制了查找强度值的复杂性。最后，这里的比较在空间上受到限制，因此亮度变化只需要局部一致。根据上面所示的采样模式和距离阈值，我们得到一个长度为512的位串。BRIEF64的位串也包含512位，因此根据定义，描述符对的匹配将同样快地执行。

3.3.  描述符匹配

匹配两个BRISK描述符是对它们的汉明距离的简单计算，就像BRIEF[4]中所做的那样:两个描述符中不同的比特数是它们不相似的度量。请注意，各自的操作减少为逐位异或，然后是位计数，这两个操作在当今的体系结构上都可以非常有效地计算。

3.4. 实施说明

在这里，我们对一些实现问题进行了非常简短的概述，这些问题对整体计算性能和方法的可重复性有很大的影响。所有的BRISK功能都建立在OpenCV 2.2的公共2D功能界面上，允许与现有功能(SIFT、SURF、BRIEF等)轻松集成和互换。

检测过程使用AGAST实现[10]来计算显著性分数。非极大值抑制得益于早期终止能力，将显著性分数计算限制在最小值。构建图像金字塔使用了一些SSE2和SSSE3命令，包括半采样和1.5倍的下采样。

为了有效地利用采样模式检索灰度值，我们生成了一个离散旋转和缩放的BRISK模式版本的查找表(包括采样点位置和高斯平滑核的属性以及长距离和短距离配对的索引)，消耗了大约40MB的RAM——这对于计算能力有限的应用程序仍然是可以接受的。

我们进一步使用积分像和一个简化的高斯核版本，灵感来自[2]:当改变σ时，核是可扩展的，而不会增加计算复杂度。在我们最终的实现中，我们使用一个简单的具有浮点边界和边长ρ = 2.6·σ的方盒均值滤波器作为近似。

因此，我们不需要使用许多不同内核对整个图像进行费时的高斯平滑处理，而是使用任意参数σ检索单个值。

我们还集成了改进的SSE汉明距离计算器，实现了当前OpenCV实现速度的6倍，例如在OpenCV中使用BRIEF。

4  实验

我们提出的方法已经按照现今建立的评估方法和数据集在Mikolajczyk和Schmid[12，13]首先提出的领域中进行了广泛的测试。为了与其他著作中的结果保持一致，我们还使用了可在线获得的MATLAB评估脚本。每个数据集都包含六个图像序列，这些序列显示出不断增加的变换量。此处所有比较都是针对每个数据集中的第一个图像进行的。图4显示了每个分析的数据集的一张图像。

转换包括视点更改（Graffiti and Wall），缩放和旋转（Boat），模糊（Bikes and Trees），亮度更改（Leuven）以及JPEG压缩（Ubc）。由于视点变化场景是平面的，因此所有序列中的图像对都具有用于确定相应关键点的地面真实单应性。在本节的其余部分中，我们将提供与SIFT（OpenCV2.2实现）和SURF（原始实现）相比的BRISK的检测器和描述符性能的定量结果。我们的评估使用相似度匹配，即将描述符距离低于特定阈值的任何一对关键点都视为匹配——与例如最近邻居匹配，在其中搜索数据库以查找具有最低描述符距离的匹配。最后，我们还列出了比较时间，以此证明BRISK在计算速度上的巨大优势。

1）BRISK检测器重复性

根据Mikolajczyk和Schmid[12,13]首先提出的评估方法和数据集，我们提出的方法已经经过了广泛的测试。为了与其他工作的结果保持一致，我们还使用了他们在线提供的MATLAB评估脚本。每个数据集都包含一个由六张图像组成的序列，显示出不断增加的转换量。这里的所有比较都是针对每个数据集中的第一张图像执行的。图4为分析的每个数据集显示了一张图像。

转换涵盖了视角变化(涂鸦和墙壁)，缩放和旋转(船)，模糊(自行车和树)，亮度变化(鲁汶)以及JPEG压缩。由于视点变化场景是平面的，所有序列中的图像对都具有地面真值单应性，用于确定相应的关键点。在本节的其余部分，我们将介绍与SIFT (OpenCV2.2实现)和SURF(原始实现)相比，BRISK的检测器和描述符性能的定量结果。我们的评估使用相似匹配，它将描述符距离低于某个阈值的任何关键点对视为匹配-与之相反，例如，最近邻居匹配，在数据库中搜索描述符距离最低的匹配。最后，我们还通过列出比较计时来证明BRISK在计算速度方面的巨大优势。

图4.用于评估的数据集:视点变化(涂鸦和墙壁)、缩放和旋转(船)、JPEG压缩(Ubc)、亮度变化(鲁汶)和模糊(自行车和树木)。

4.1.BRISK检测器的重复性

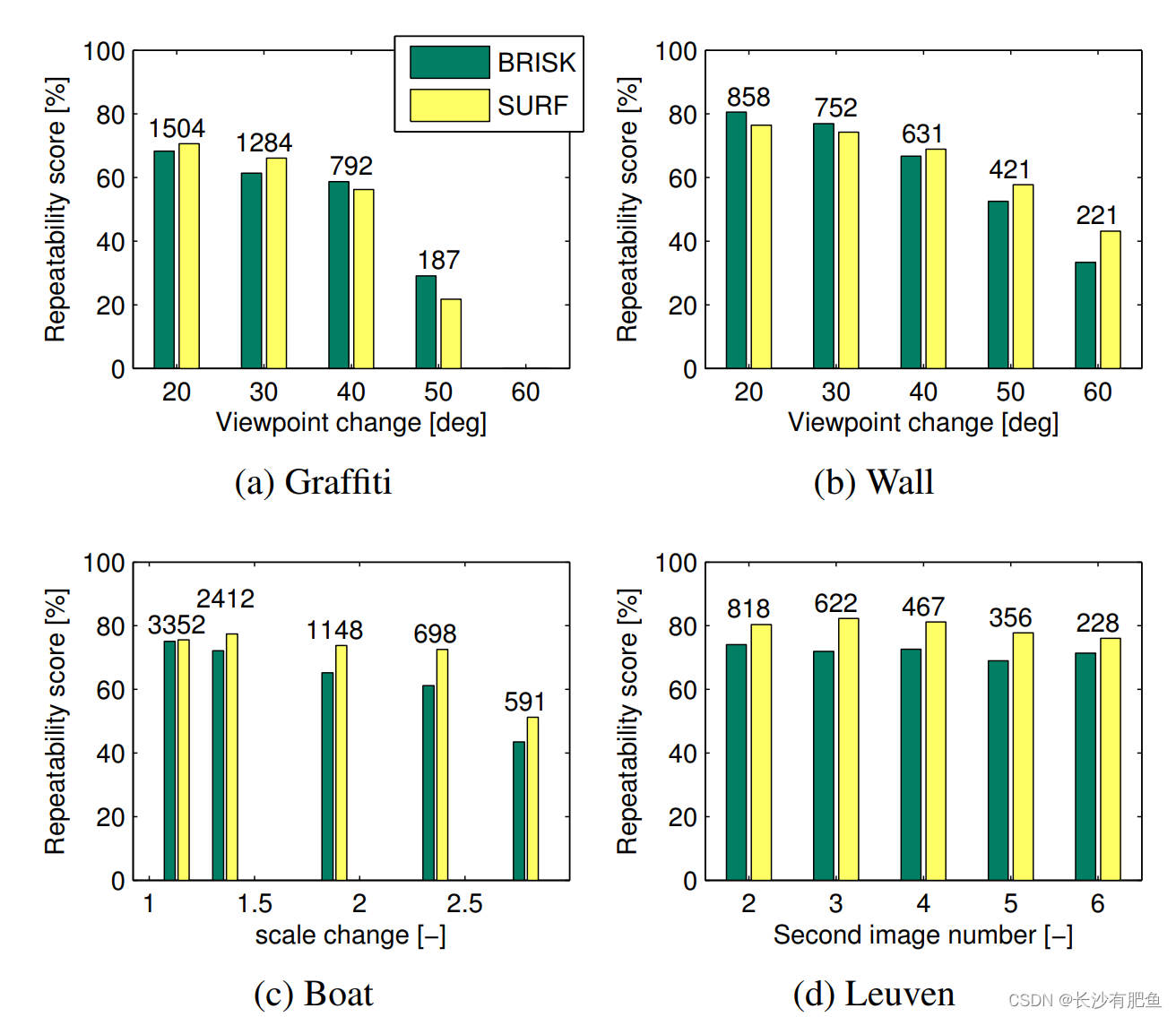
在[13]中定义的检测器可重复性分数计算为对应关键点与两个图像中可见关键点的最小总数之间的比率。通过观察一个图像中关键点区域的重叠区域(即提取的圆)和另一个图像中关键点区域的投影(即类椭圆)来识别对应关系:如果交集区域大于两个区域并集的50%，则认为它是对应关系。注意，这种方法在很大程度上依赖于关键点圆半径的分配，即比例尺和半径之间的常数因子。我们选择这样的平均半径获得的BRISK探测器大致匹配平均半径获得的SURF和SIFT探测器。

重复性评分的评估(结果的选择如图5所示)是在一个序列上使用恒定的BRISK检测阈值来执行的。为了与SURF检测器进行公平的比较，我们调整了各自的Hessian阈值，以便在基于相似性的匹配设置中输出大约相同数量的对应。

如图5所示，只要应用的图像变换不是太大，BRISK检测器表现出与SURF检测器相同的可重复性。然而，考虑到BRISK在计算成本上优于SURF探测器的明显优势，所提出的方法构成了一个强大的竞争对手，即使在较大的转换时性能似乎略逊一筹。

图5.重复性得分为50%的重叠误差的BRISK和SURF探测器。由此产生的相似度对应(探测器之间的近似匹配)以柱上的数字表示。

4.2.整体BRISK算法的评价与比较

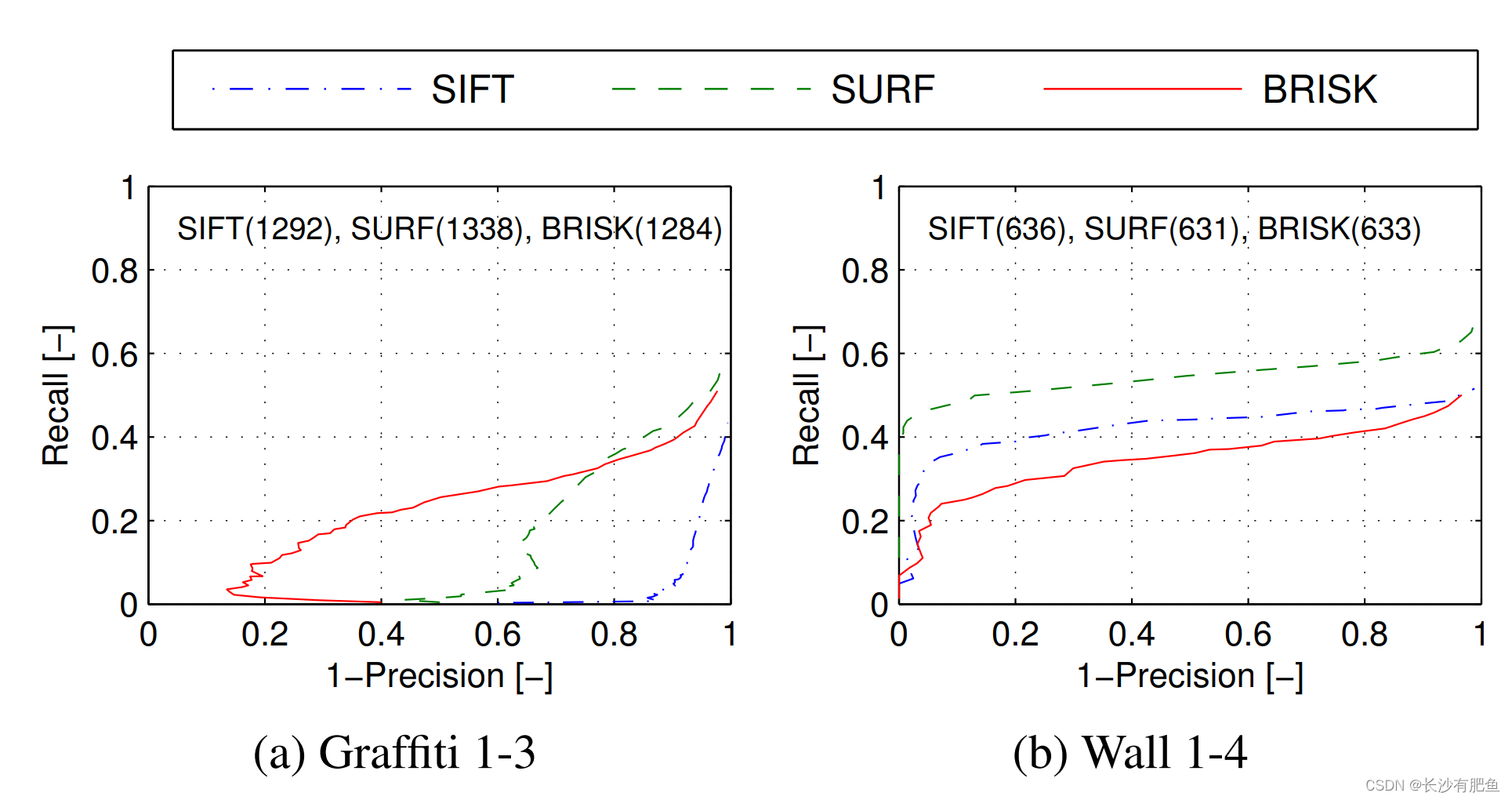
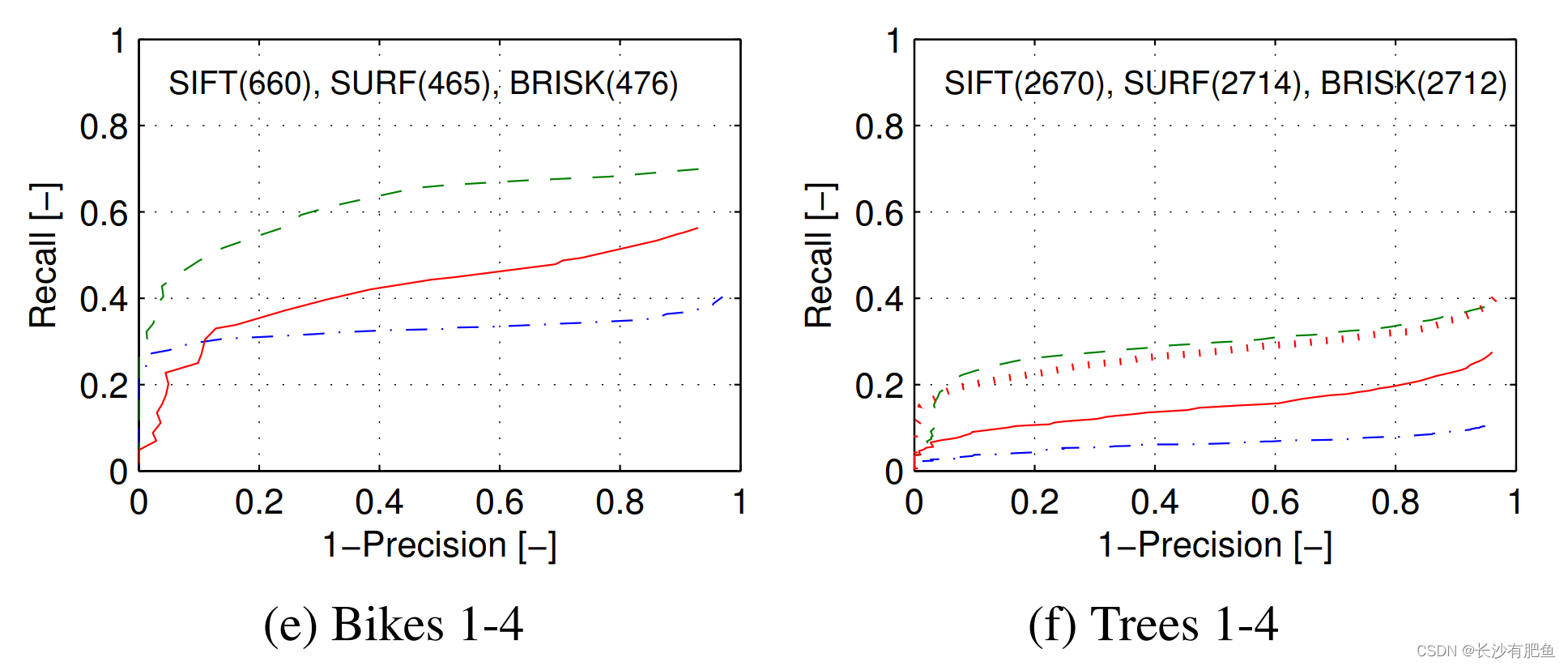
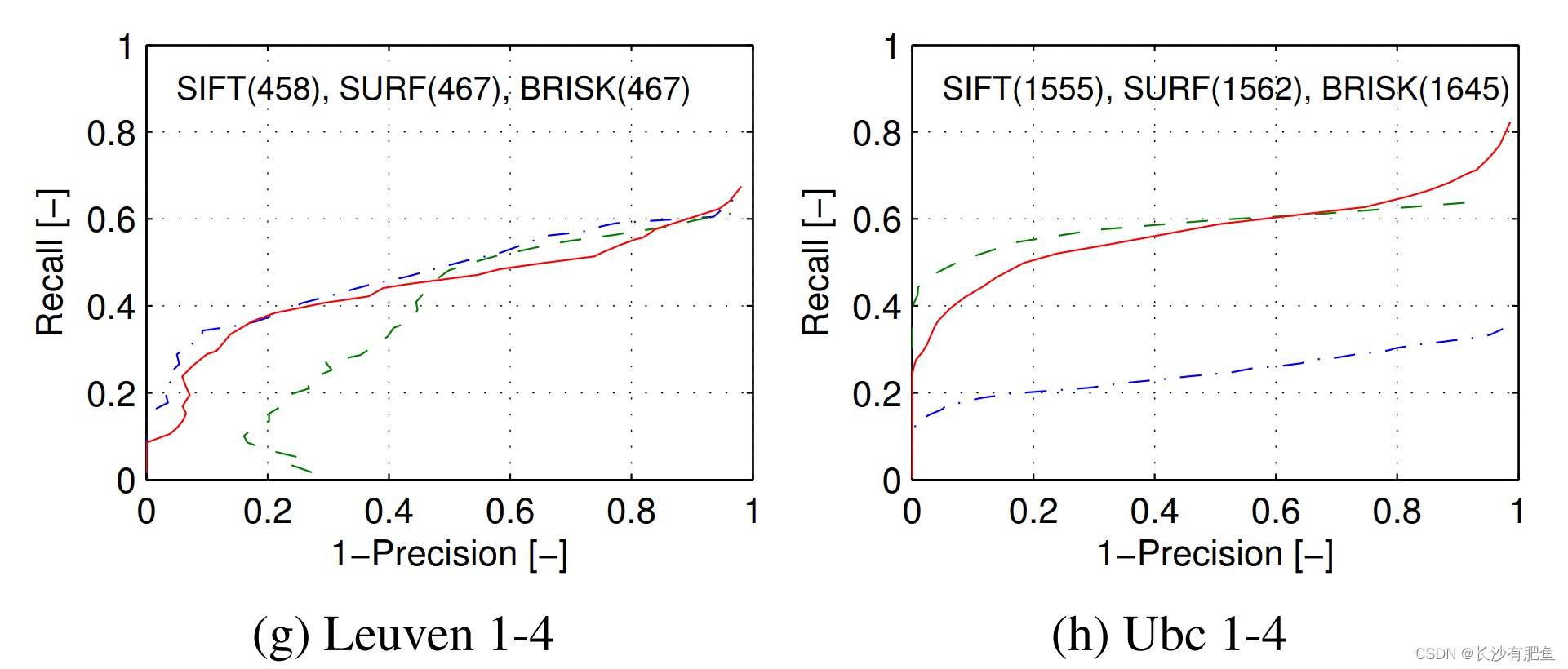
由于我们的工作旨在提供一个整体快速且健壮的检测、描述和匹配，我们评估了在BRISK中所有这些阶段的联合性能，并将其与SIFT和SURF进行比较。图6显示了对不同数据集的图像对使用基于阈值的相似匹配的精度召回曲线。同样，对于这个评估，我们调整检测阈值，以便它们在公平的精神下输出大约相等数量的通信。请注意，这里的评估结果与[3]中的结果不同，在[3]中，所有描述符都是在相同的区域上提取的(使用Fast-Hessian检测器获得)。

如图6所示，在所有数据集中，BRISK都能与SIFT和SURF进行竞争，在某些情况下甚至优于其他两个。在Trees数据集中，BRISK的性能下降归因于检测器的性能:虽然SURF在图像中分别检测到2606和2624个区域，但在图像4中，BRISK仅检测到2004个区域，而在图像1中发现了5949个区域，以实现大致相同的对应数量。同样的情况也适用于另一个模糊数据集，Bikes:用FAST评估的显著性本质上比blob-like检测器对模糊更敏感。因此，我们还展示了对从SURF区域提取的树数据集的BRISK描述符的评估，再次证明了描述符的性能与SURF相当。另一方面，SIFT和BRISK对纯平面内旋转的重要情况处理得非常好，优于SURF。

图6.评价结果显示的精度-召回曲线(所有检测，提取和匹配阶段的联合)为BRISK, SURF和SIFT。结果显示视点变化(a和b)，纯平面内旋转(c)，缩放和旋转(d)，模糊(e和f)，亮度变化(g)和JPEG压缩(h)。每个算法的相似对应数在图中表示。(f)中的红色虚线显示了从SURF区域提取的BRISK描述符的性能，产生了2274个对应。总体而言，BRISK在所有情况下都表现出具有竞争力的性能，在某些情况下甚至优于SIFT和SURF。

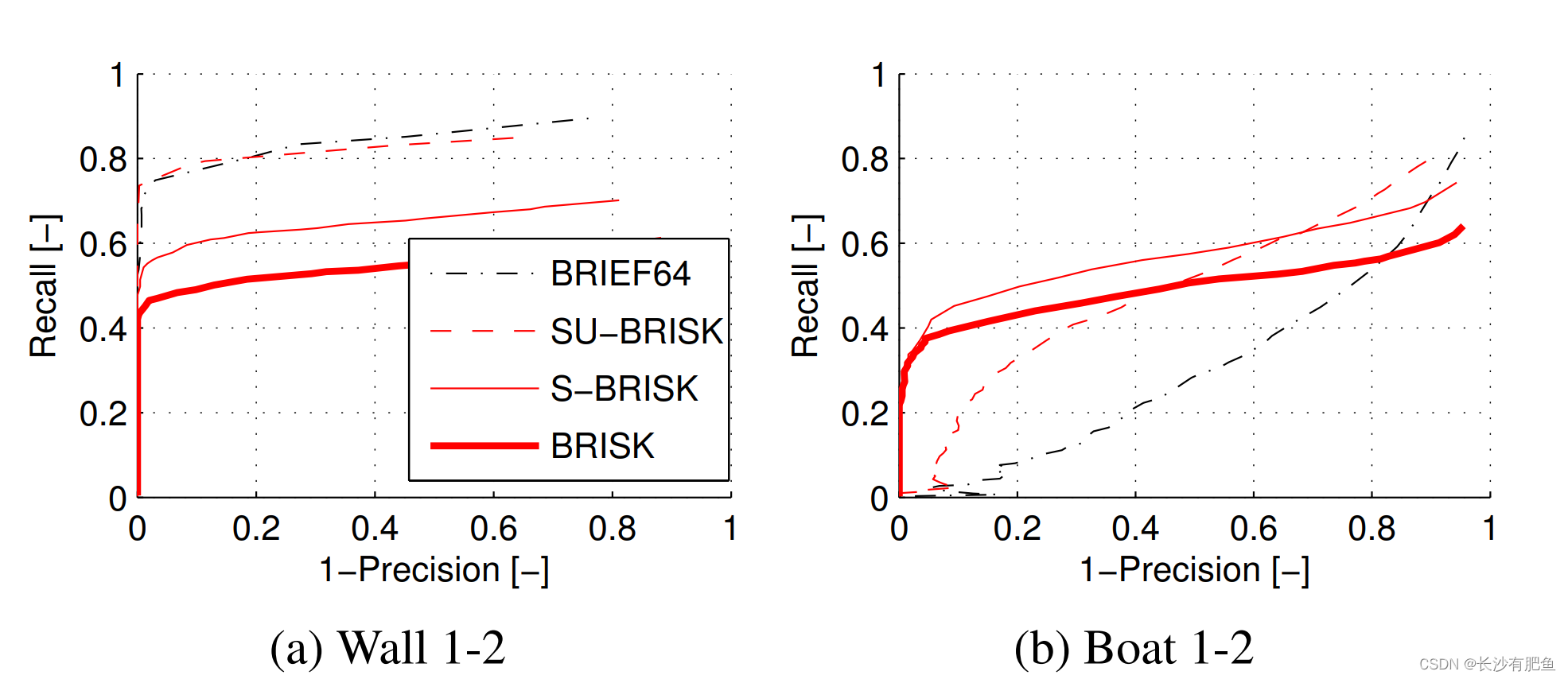
为了完成实验部分，我们想做一个BRIEF链接。图7显示了在相同(单尺度)AGAST关键点上，未旋转的单尺度BRISK版本(SU-BRISK)与64字节BRIEF特征的比较。还包括旋转不变量，单尺度S-BRISK，以及标准的BRISK。实验是用两张图像对进行的:一方面，我们使用Wall数据集中的前两张图像证明，在没有尺度变化和平面内旋转的情况下，SU-BRISK和BRIEF64表现出非常相似的性能。注意，这正是设计BRIEF的目的。另一方面，我们将不同的版本应用于船序列的前两个图像:这个实验证明了SUBRISK在小旋转(10◦)和比例变化(10%)的稳稳性方面优于BRIEF的一些优势。此外，众所周知的和直观的价格旋转和规模不变性是很容易观察到的。

图7.不同的BRISK版本与64字节BRIEF的比较。从原始图像中检测到的AGAST关键点中提取出BRIEF，以及SU-BRISK(单尺度，未旋转)和S-BRISK(单尺度)。注意，BRISK模式的大小与BRIEF补丁大小相匹配。标准版本的BRISK必须从我们的标度不变角检测中提取出来，使用适应的阈值来匹配对应的数量:在Wall对中是850个，在Boat对中是1530个。

4.3.时间

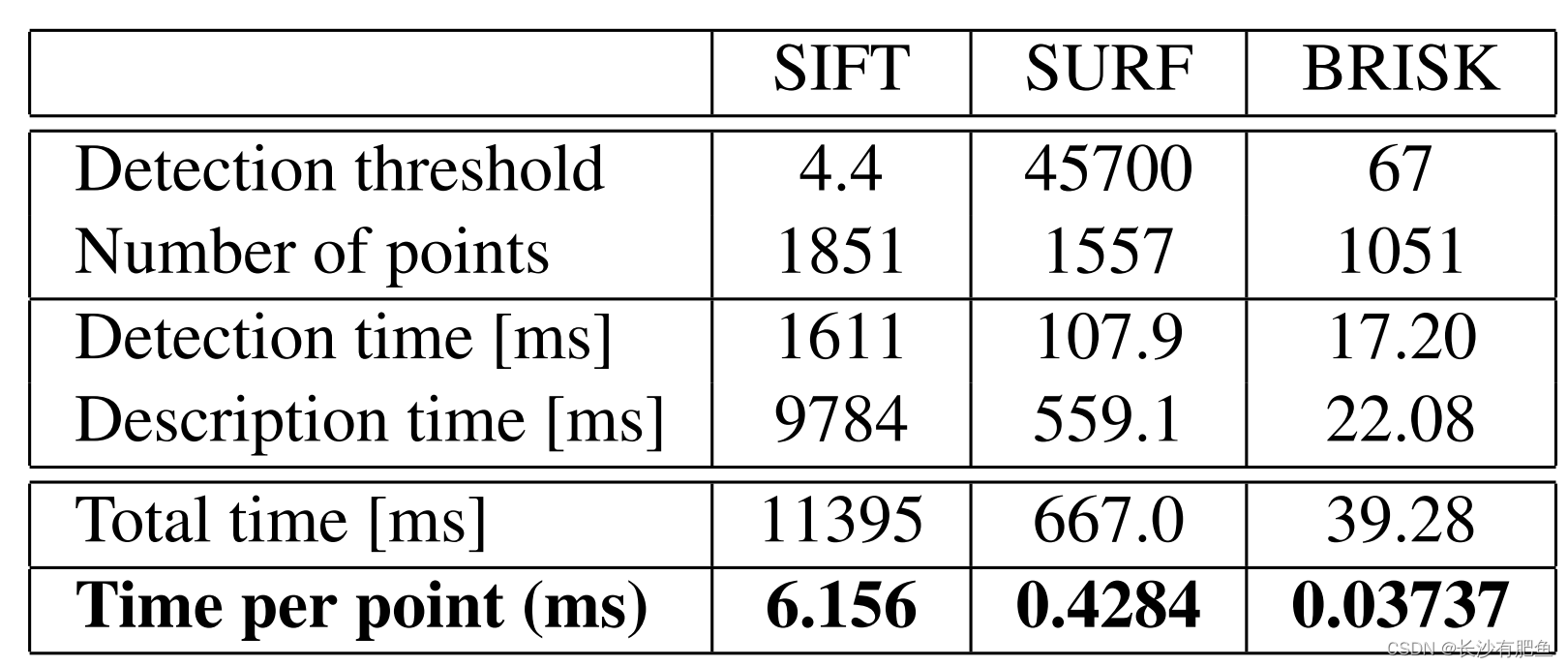
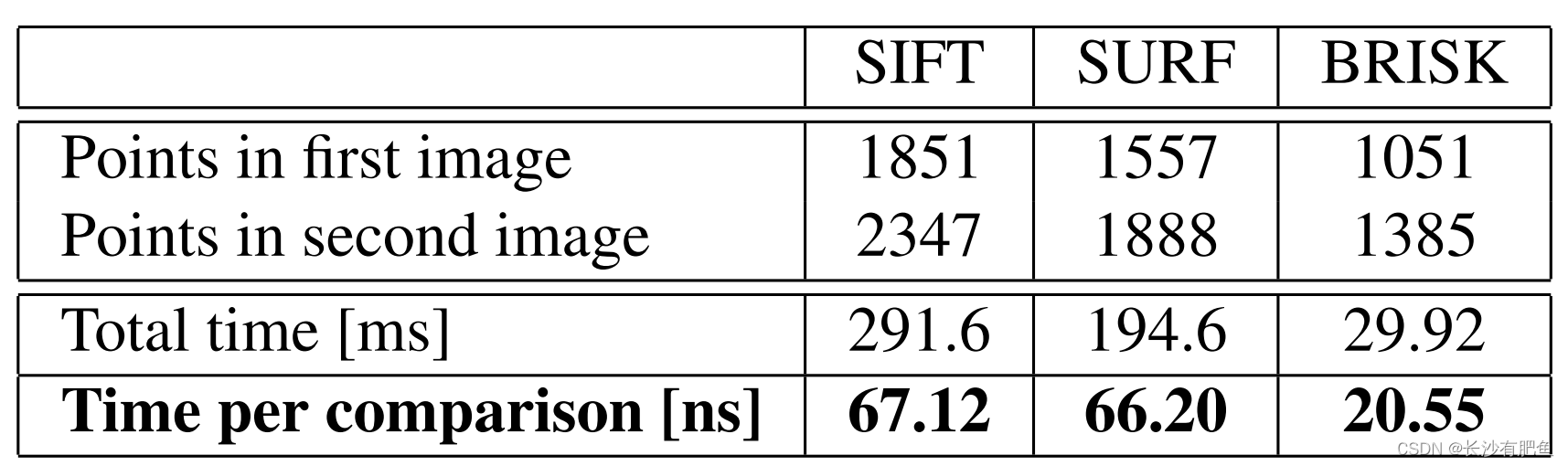
计时已经在一台运行Ubuntu 10.04(32位)的四核i7 2.67 GHz处理器的笔记本电脑上记录，使用如上所述的实现和设置。表1给出了涂鸦序列第一张图像的检测结果，表2给出了匹配次数。这些值在100次运行中取平均值。请注意，所有匹配器都执行蛮力描述符距离计算，而不进行任何早期终止优化。

时间显示了BRISK的明显优势。它的检测和描述子计算通常比SURF快一个数量级，SURF被认为是目前可用的最快的旋转和尺度不变特性。同样重要的是要强调的是，通过减少模式中采样点的数量，以匹配质量为代价(这在特定的应用程序中可能是负担得起的)，BRISK可以轻松地扩展以实现更快的执行。此外，缩放和/或旋转不变性可以被忽略，在不需要它们的应用程序中提高了速度和匹配质量。

表1.涂鸦序列(大小:800 × 640像素)中第一张图像的检测和提取时间。

表2.匹配的时间为涂鸦图像1和3设置。

4.4.一个例子

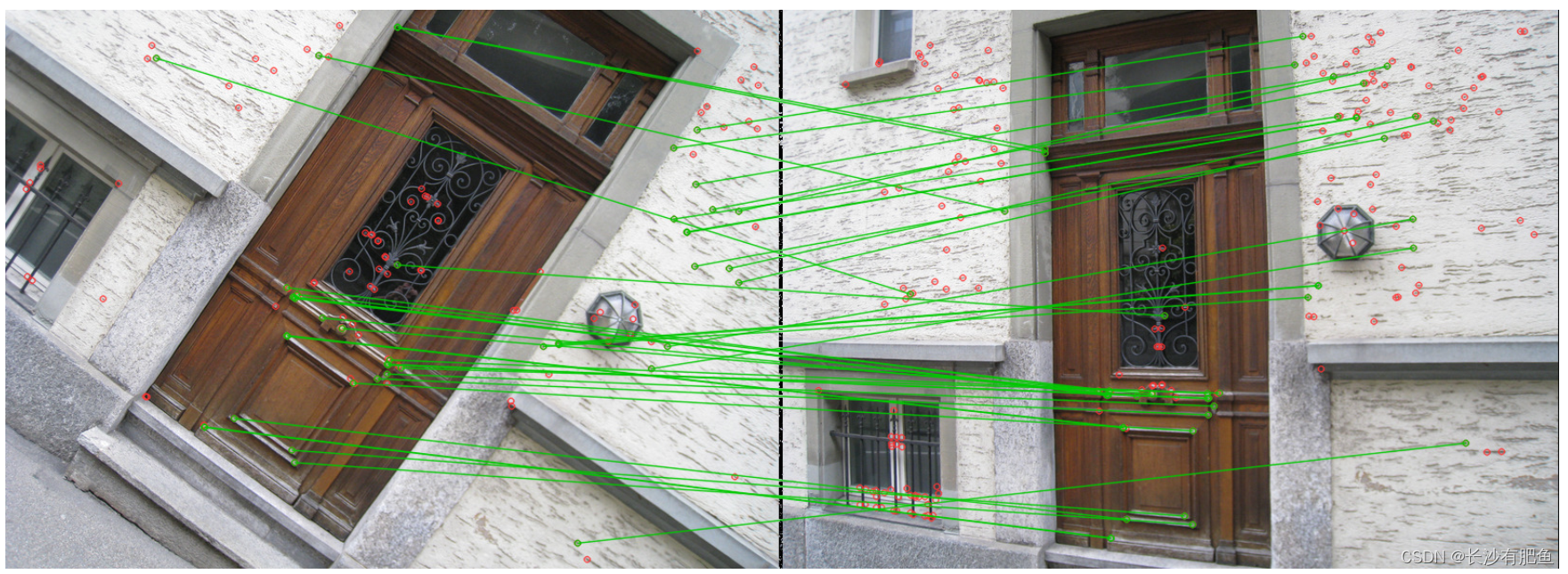
作为上述广泛评估的补充，我们还提供了一个使用BRISK进行匹配的真实示例。图8显示了显示各种转换的图像对。执行阈值为90的相似性匹配(在512个比较中)，从而得到没有显著异常值的鲁棒匹配。

图8.BRISK匹配示例:检测阈值为70，匹配的汉明距离阈值为90。结果匹配由绿线连接，显示没有明显的假阳性。作者提供了一个可从

http://www.asl.ethz.ch/people/lestefan/personal/BRISK下载的BRISK参考实现。

5 结论

我们提出了一种名为BRISK的新方法，它解决了经典的计算机视觉问题，即在没有足够的场景和相机姿态先验知识的情况下检测、描述和匹配图像关键点。与已被证明具有高性能的成熟算法(如SIFT和SURF)相比，手头的方法在相当的匹配性能上提供了一个更快的替代方案——这是我们基于使用已建立的框架进行广泛评估的结论。BRISK依赖于一个易于配置的循环采样模式，从中计算亮度比较以形成二进制描述符字符串。BRISK的独特属性可以用于广泛的应用程序，特别是具有硬实时约束或计算能力有限的任务:在这种时间要求高的应用程序中，BRISK最终提供了高质量的高端功能。

在对BRISK进行进一步研究的途径中，我们的目标是探索显著性分数的尺度空间最大值搜索的替代方案，以在保持速度的同时产生更高的重复性。此外，我们的目标是在理论上和实验上分析BRISK模式和比较的配置，以便使描述子的信息内容和/或鲁棒性最大化。

6 致谢

这项研究是由自主系统实验室，苏黎世联邦理工学院和欧盟委员会第七框架计划(FP7/2001-2013)支持的。231855 (sf)。我们感谢Simon Lynen和Davide Scaramuzza的宝贵意见，也感谢苏黎世联邦理工学院的许多其他同事进行了非常有帮助的讨论。