905. 按奇偶排序数组

-
1)额外数组 + 两次遍历,第一遍将所有的 偶数 放到结果数组 res 的前面,第二遍将所有的 奇数 接着放到结果数组 res 的后面。也可以使用 对撞指针 往结果数组里存,在 一次遍历 内搞定。
-
2) 对撞指针 , 从 左边 不断的找到 第一个 奇数 , 从 右边 不断的找到第一个 偶数 ,找到就交换 左边 和 右边 。不断重复以上过程。原地算法,空间O(1)。


解题思路:
- 3)快排二路分区逻辑,参考快排中分区交换的逻辑来处理,快排分区逻辑中是将比分区点小的交换到左边,将比分区点大的交换到右边,而本题可以认为是按奇偶性进行排序,将偶数交换到左边,将奇数交换到右边。
快排二路分区逻辑有两种版本,一种是使用对撞指针的版本,另一种是使用快慢指针的版本。
对撞指针的二路分区版本:

这个版本其实跟上面的方法 2)本质上是一样的。
快慢指针的二路分区版本:

这个版本只能算是快排二路分区快慢指针版本的变形,并不是严格的分区逻辑。
922. 按奇偶排序数组 II

-
1) 额外数组 + 遍历原数组 ,将 偶数 放到新数组的偶数下标位置上 i = 0,i += 2 ,将 奇数 放到新数组的奇数下标位置 上 j = 1,j += 2。
-
2 ) 双指针 + 原地处理, i 指向偶数下标 i = 0 , j 指向奇数下标 j = 1 ,遍历数组的每一个 偶数位 , i += 2 ,如果在 偶数位 上发现一个 奇数 时,就不停的 while 尝试在 奇数位 上找到一个 偶数 , j += 2 ,如果找到就交换二者swap(i, j)。


注意 i 和 j 的步长都要 + 2,因为奇偶下标都是间隔的。
88. 合并两个有序数组
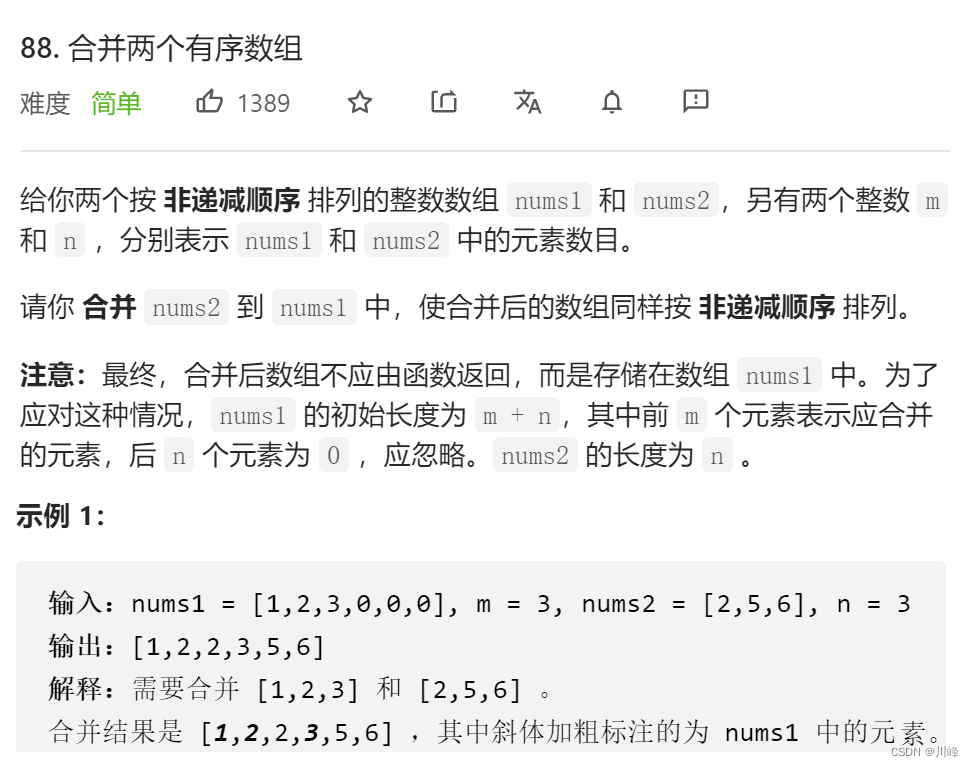
-
1) 额外数组,参考 归并排序 中合并两个有序数组的过程,设指针 i 和 j 分别指向 nums1 和 nums2 ,然后比较二者 较小 的值存到 tmp 数组中,最后再将 tmp 数组拷贝到原数组。 空间O( m+n ) 时间 O(m+n)

不过题目中 nums1 预留了额外空间,很显然是要原地修改,而不是使用额外空间。
-
2) 三指针逆向存取 ,设 i、 j、k 分别指向 nums1、 nums2、结果数组 的末尾, 遍历时从 nums1 和 nums2 屁股后面开始取值,谁 大 就把谁安排到 结果数组 的屁股后面(本题 结果数组 就是 nums1 )。 然后分别把较大的指针和结果数组的指针 前移 一个。
-
如果有一个取到空了,就把另一个剩余的全部逆序放入 nums1 中。
-
循环条件是 nums1 和 nums2 的指针有一个没到头就继续 。
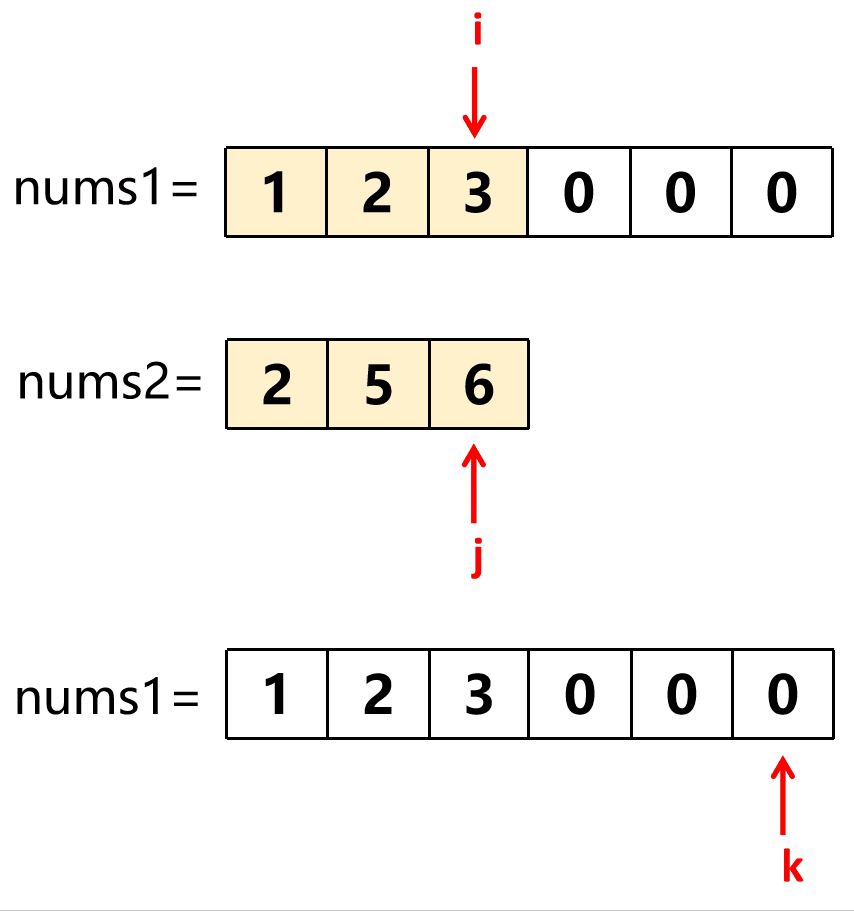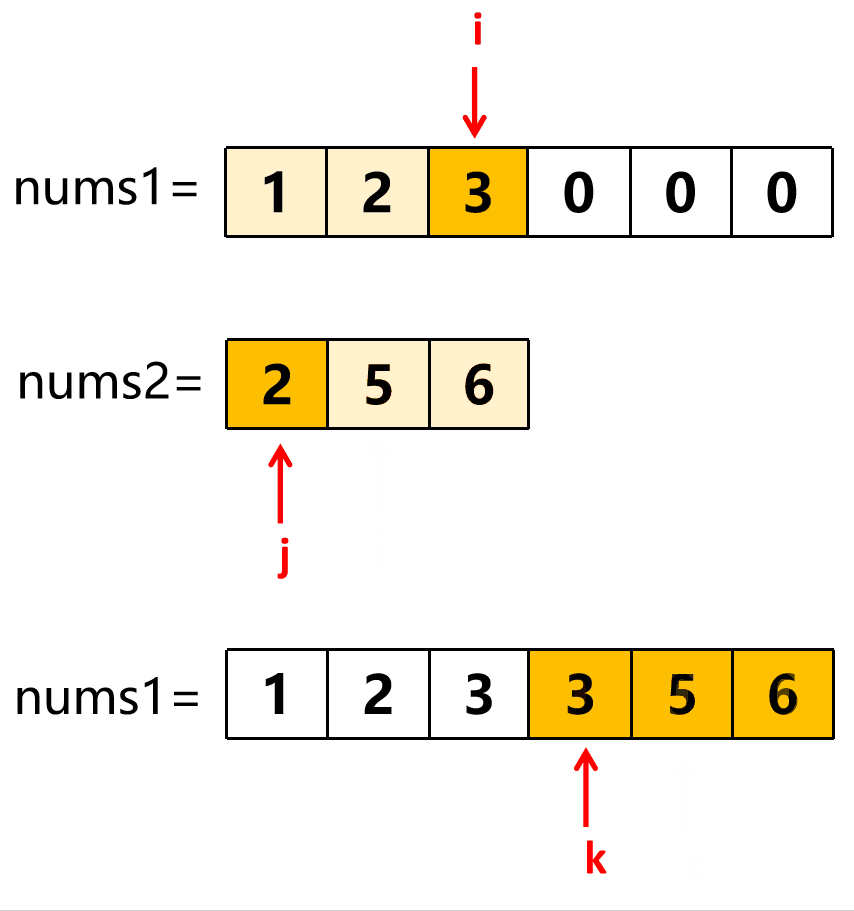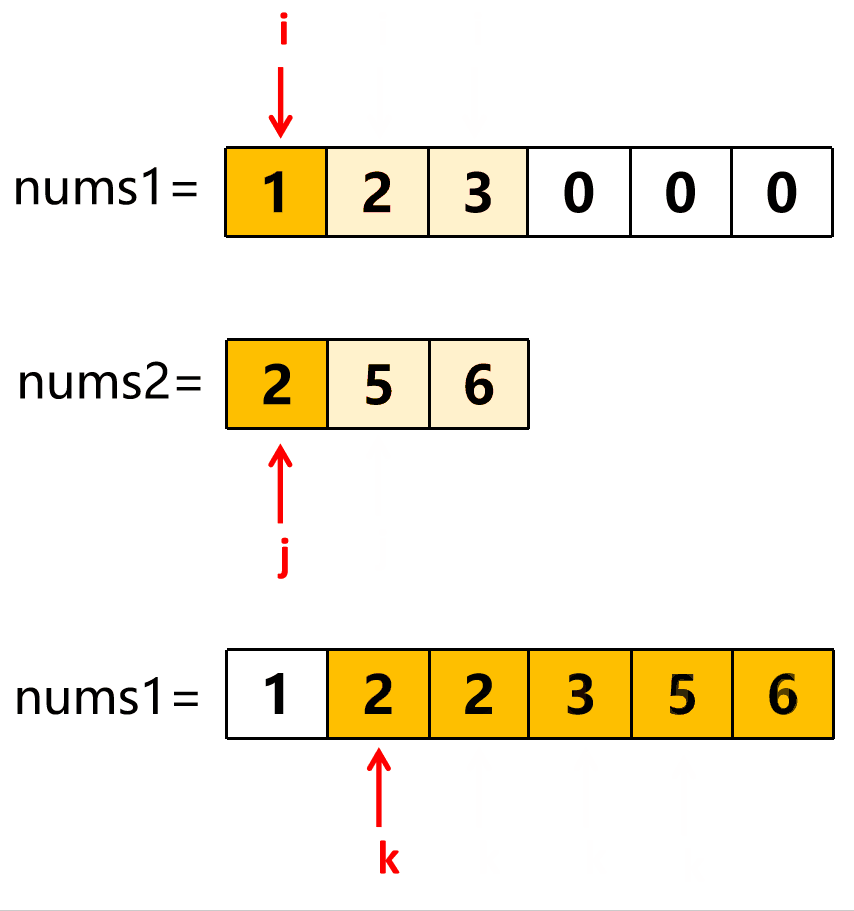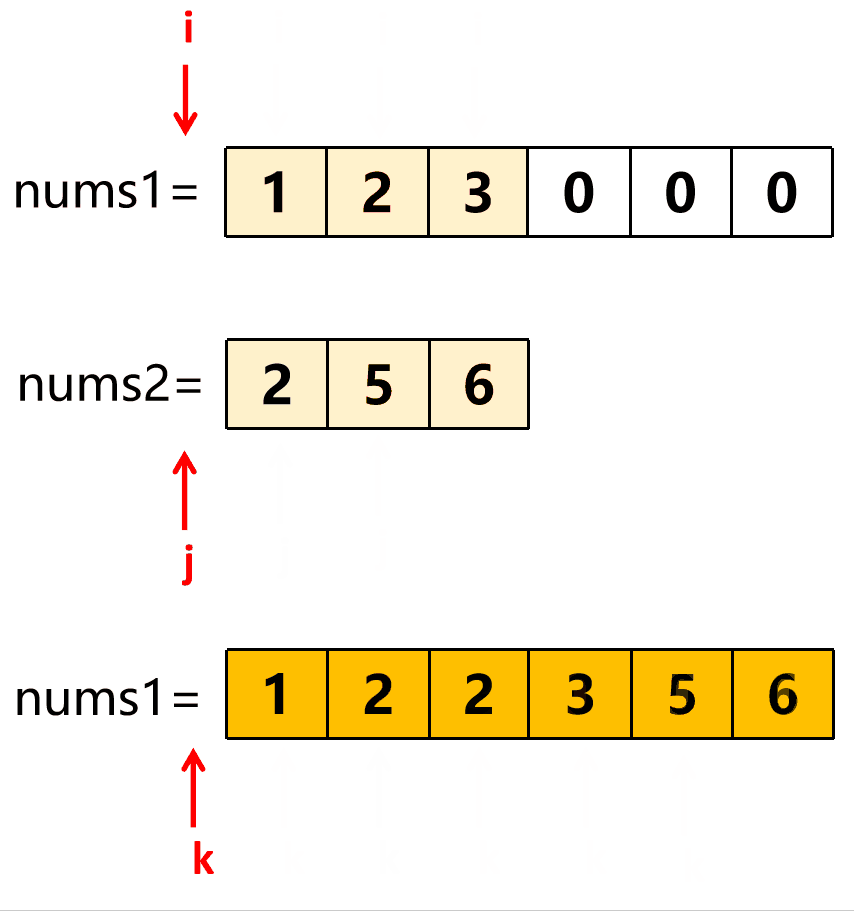

当 nums1==nums2[j] 时,代码中取谁都无所谓,不会影响最终结果。
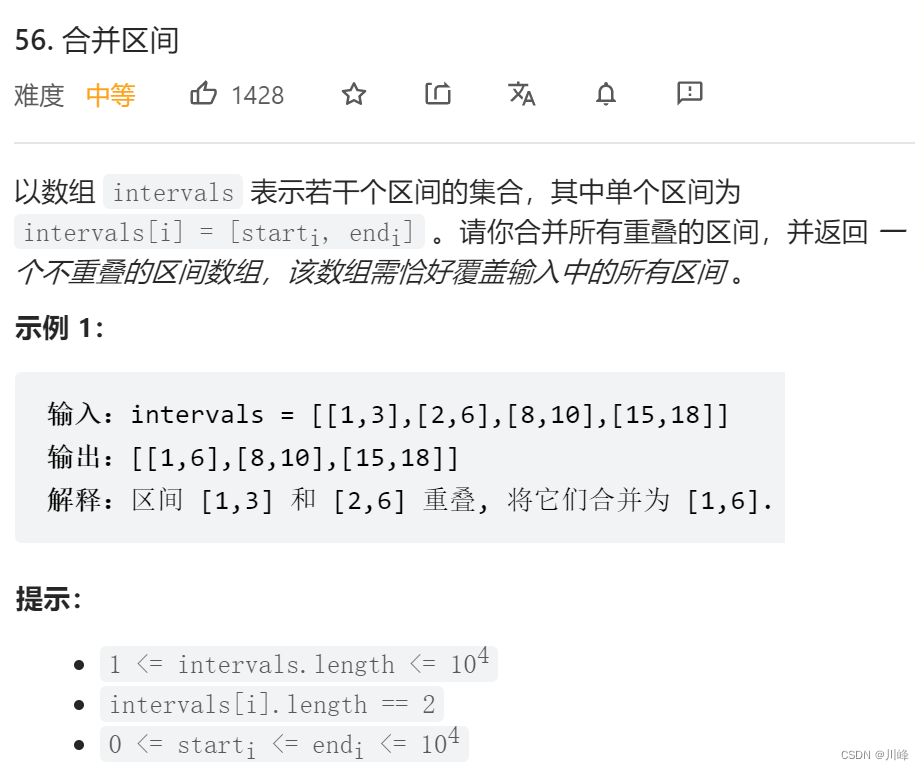
56. 合并区间
-
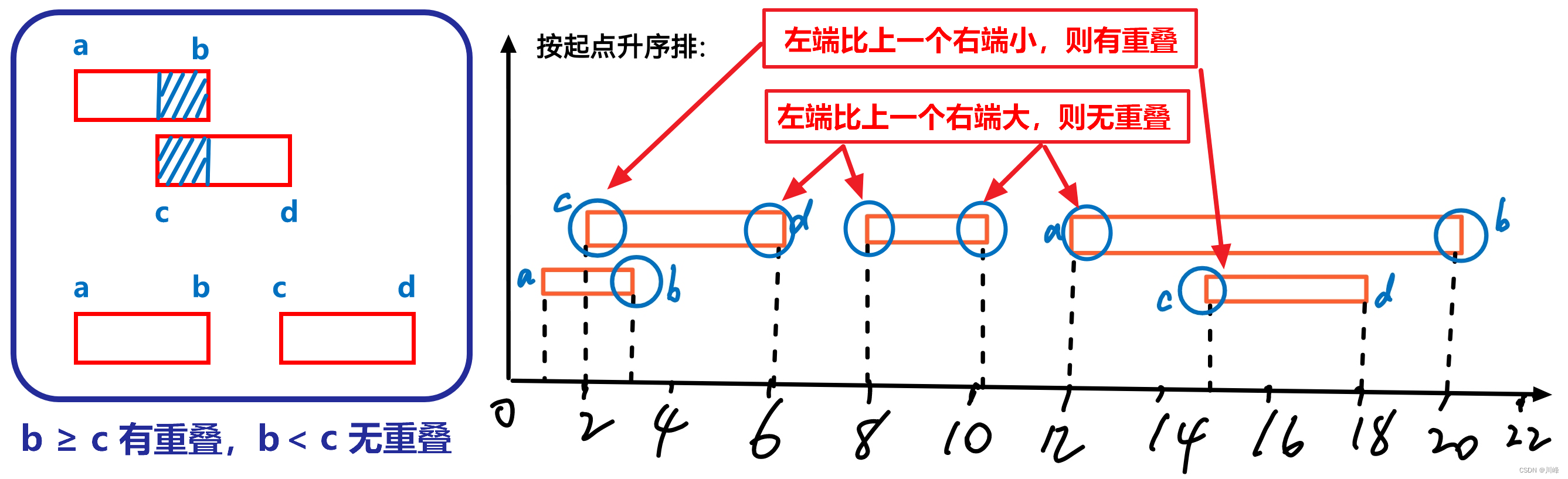
按照区间左端点升序排序 ,然后遍历所有的区间,依次比较 当前区间 与合并 结果集合 中的 前一个区间 是否有重叠,如果无重叠就直接把当前区间收集到结果集合中,如果有重叠就把当前区间合并到前一个区间中。
-
判断 当前区间 与 前一个区间 是否有重叠的方法:
-
前一个区间 的 右端点 < 当前区间 的 左端点 ,则 无重叠 , 前一个区间 的 右端点 > = 当前区间 的 左端点 ,则有重叠 。 例如考虑左端点两个升序排列的两个区间 [a, b] [c, d] : 若 b < c 则无交集,若 b >= c 则有交集,如果有交集,则 交集的左边界 = a, 交集的 右边界 = max(b, d)

57. 插入区间

-
1)观察 插入区间 和 原始区间 左右边界的关系 ,可得 不重叠 的条件是: 原区间.右 < 插入区间.左 或 原区间.左 > 插入区间.右 。
-
先分别找出 重叠开始 和 结束 的区间索引,当然,也有可能插入的区间与所有原始区间都没有重叠(此时找不到重叠开始和结束的区间索引,记为-1)。
-
我们可以分成以下两大类情况处理:
-
① 插入区间与原始区间 有重叠 的情况,我们需要 合并重叠 的区域,然后按照 重叠之前、合并、重叠之后 的顺序添加区间。
-
② 插入区间与原始区间 无重叠 的情况,就先直接添加 原始所有区间 ,并记录应该插入新区间的位置,最后再插入新区间即可。



这里如果 start == -1,则 end 一定也等于 -1,如果 start != -1,则 end 也一定不等于 -1,所以只需要是否重叠判断 start 是否为 -1 即可。
另外在无重叠情况下,查找插入位置,其实就是在一个有序数组中查找第一个比插入目标大的位置(因为题目给定的区间是已经按照左端点升序排序好了的),例如 1,2,3,7,9 中插入 5 我们应该找到 7 的位置,将 5 插入该位置,原来的 7 和 9 分别后移。
解题思路:
- 2)分成三个阶段来考察
- ① 先将 区间右边界 < 插入区间左边界 的区间放入到结果集,这些区间与插入区间无重叠
- ② 将 区间左边界 ≤ 插入区间右边界 && 区间右边界 ≥ 插入区间左边界 的区间和插入区间进行合并,然后把合并的区间放入到结果集
- ③ 将剩余的区间放入结果集,这些区间与插入区间无重叠


252. 会议室
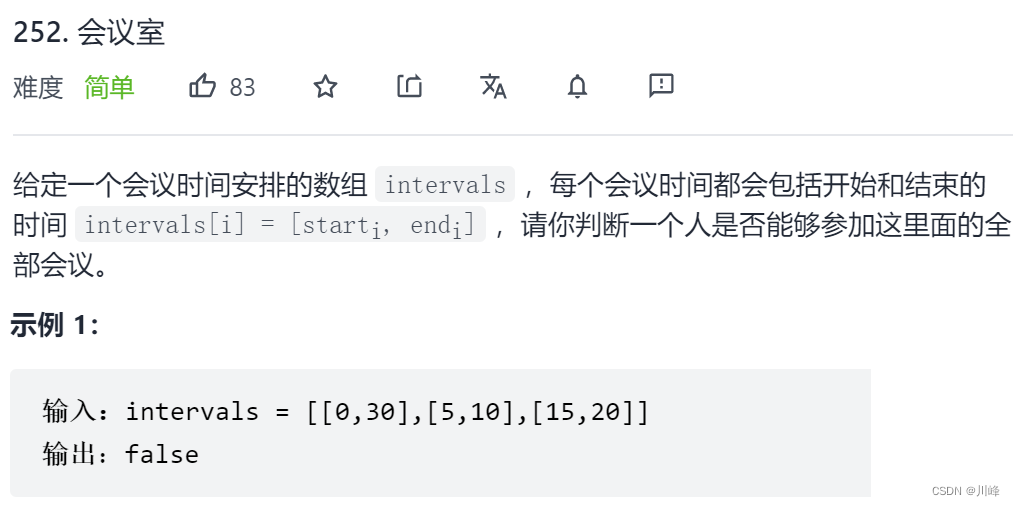
解题思路:
-
同56,只需要 判断区间是否有重叠 的即可,一旦有重叠的两个会议时间段,就不能全部参加了。
-
先 按照区间左端点升序排序 ,然后遍历所有的区间, 比较 [a, b] [c, d] 中是否有 b > c 的情况, 即 前一个会议 的 结束时间 大于 当前会议 的 开始时间 ,那么就冲突了。
-
注意:本题中 b == c 是允许的,因为在前一个会议恰好结束时开始下一个会议是可以的。

253. 会议室 II

-
1. 转化为公交车上下车问题 ,某个时刻上车 +1 人,某个时刻下车 -1 人,求车上最多有几人。题目要求的其实就是可在同一时刻进行的会议的最大数量。
-
首先按照 [a, b] -> [[a, 1], [b, -1]] 格式将原始数组转化为新的二维数组,然后将新数组按照 第一维 (左端点)升序排序。
-
然后遍历排序后的新数组, 累加第二维的数量 ,并记录累加数量的 最大值 即为所求答案。
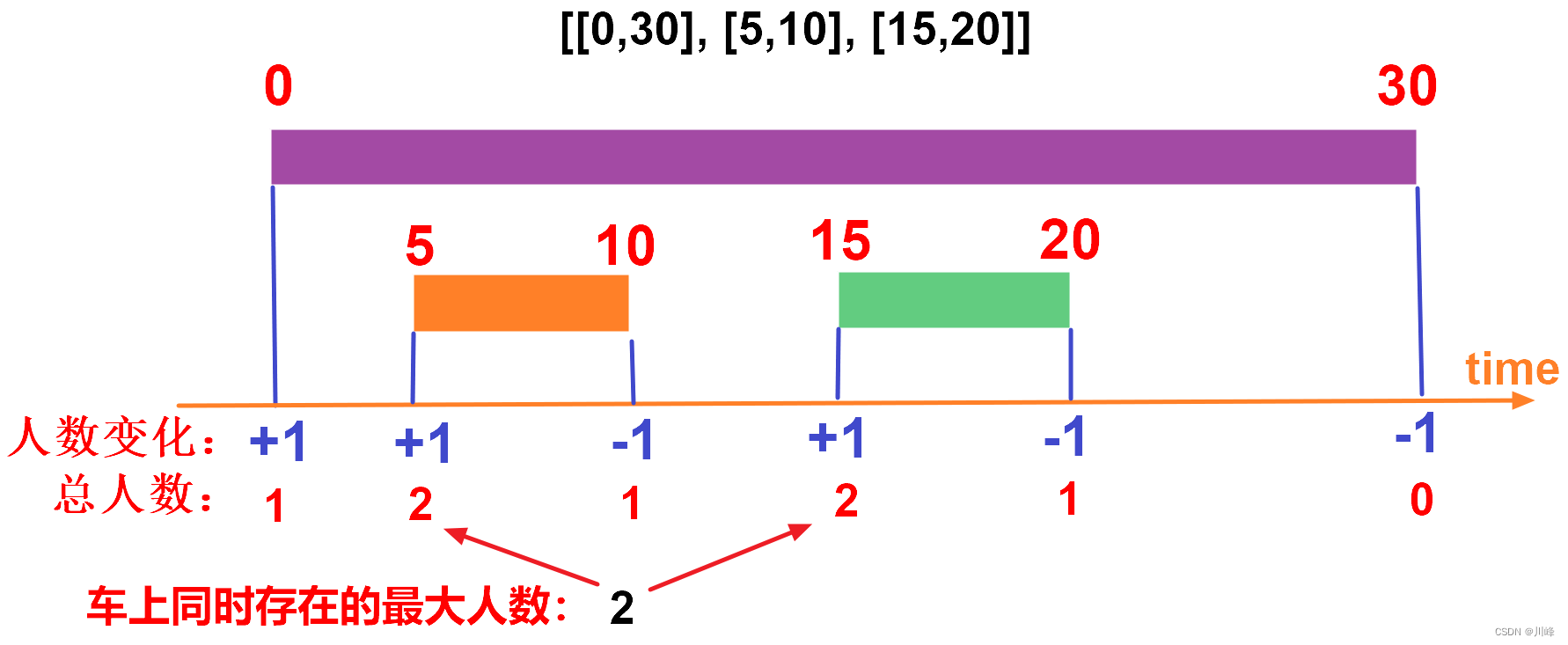


注意上面代码中对新数组排序时,一维相同时按照按二维升序排,这样是为了能保证结束时间和开始时间相同时,先下车后上车。例如 intervals = [[5, 10], [1, 5]],生成的新数组 = [[5, 1], [10, -1], [1, 1], [5, -1]],排序后变成 [[1, 1], [5, -1], [5, 1], [10, -1]],注意到中间两个相同的 5 是 -1 的排在前面。
-
2. 排序 + 小根堆 ,使用 小根堆 存储会议的 结束时间 ,这样每次取出 堆顶 的元素就是 最早结束的房间 。
-
首先,将第一个会议区间的结束时间放入小根堆中,然后遍历剩余会议,判断其与堆顶是否重叠:
-
① 如果 堆顶 的房间 不空闲 ,那么其他 所有房间 都 不可能空闲 。此时需要开一个 新房间 , 加入堆 中。(即放入当前正在处理的会议的 结束时间 )
-
② 如果 堆顶 的房间 空闲 ,则从堆顶取出该房间,将我们当前正在处理的会议的 结束时间 放入堆中。
-
这里所说的 “是否空闲” 的含义,就是指当前遍历遇到的区间与堆顶存储的结束时间是否会发生冲突/重叠。
-
处理完所有会议后, 堆的大小 即为 开的房间数量 。这就是所需要的 最小房间数 。

注意,小根堆中存储的是会议的结束时间,但是它的含义也是正在使用的会议室房间,因为如果一个会议结束时间还没有到(相对于当前遍历到的会议来说),它就要占用一个房间。因此,最后小根堆中剩下的就是需要同时占用的房间数量。
912. 排序数组 & 快排 & 归并
-
快排 - 快慢指针法


注意点:fast 只需要处理到 R - 1 即可(因为此时R是分区点),也就是说快指针的枚举区间是 [L, R) 。
另外,为什么最后还要把分区点交换回 slow 位置呢,这是因为在一趟分区交换之后,slow 位置其实就是新的分区点位置(该位置将数组分成了左边小,右边大的形式),而在快慢指针交换之前,为了方便我们将分区点的值交换到了最后的 R 位置,因此结束后需要再将分区点的值放回它应该处的位置,也就是 slow 位置。简单来说,其实就是将分区点的值放回到它该属于的位置上。
下图是力扣官方题解给出的执行动画过程,可参考理解:

快排算法的关键精髓在于分区逻辑方法,所以理解分区逻辑算法的过程至关重要:

解题思路:
-
快排 - 对撞指针法 (又叫挖坑法)
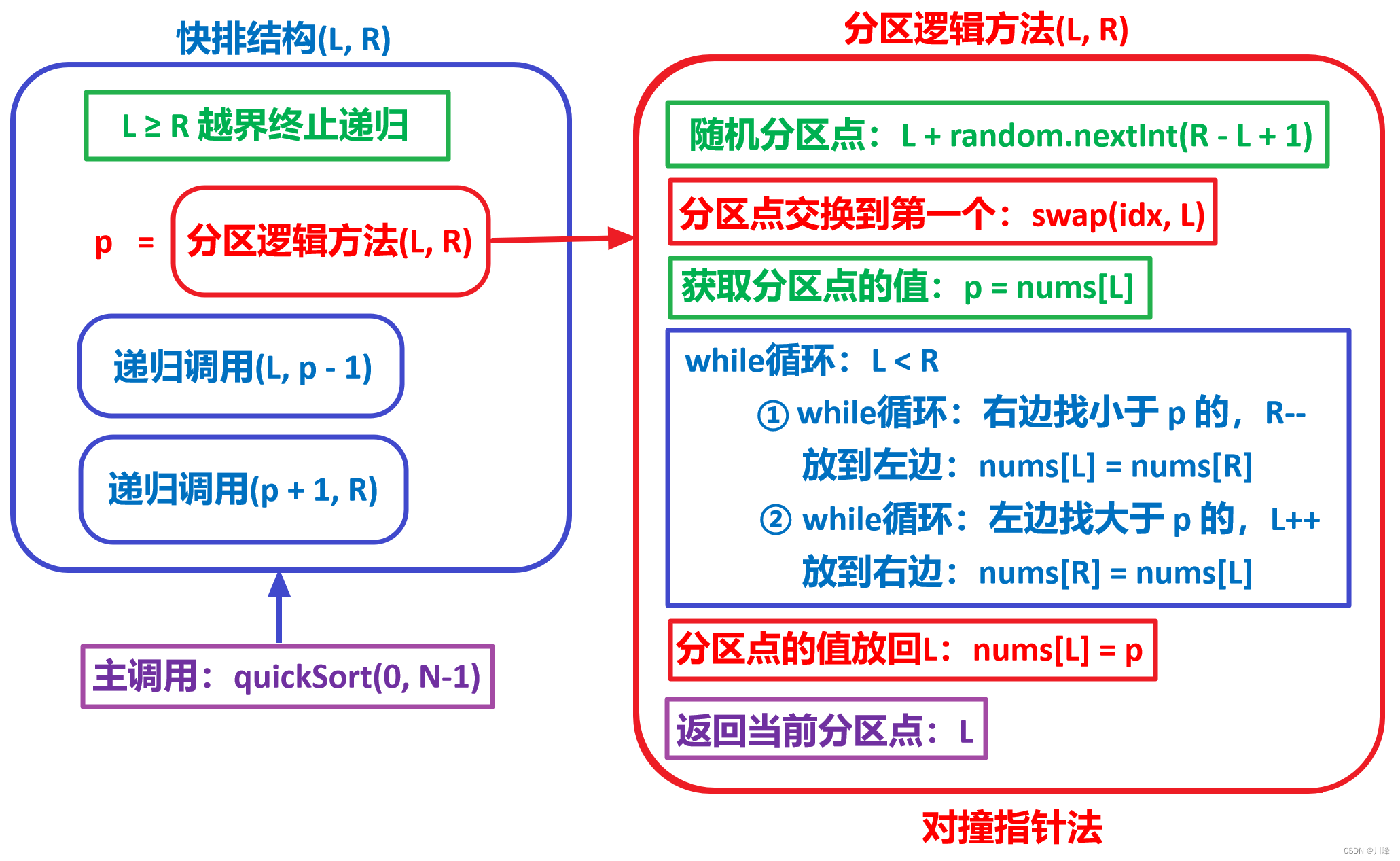
这种方法的递归调用逻辑跟快慢指针法是一样的,区别在于分区逻辑算法的不同。

这个分区交换的过程其实就是一个挖坑的过程,首先将 L 处的分区点的值记录下来,这样 L 处就预留出了一个坑位,然后从右边找一个比分区点大小的值来填充这个坑位,填充之后,右边的 R 处就又空出了一个坑位,然后从左边找一个比分区点大的值来填充这个坑位。这样循环下去,其实就是在左右开弓,不断留出坑位,不断填充坑位。最后 L 位置是实际的分区点位置,所以也需要把分区点的值放回到 L 处。
下图展示了这个大概的交换过程:

解题思路:
-
快排 - 三路分区


上面代码有一个细节需要留意,当 nums[i] > p 时,把 nums[i] 交换到 great 位置,但是 i 位置不要移动,因为从 great 位置交换过来到 i 位置上的数仍然是未处理的数,[i, great] 都是未处理的区域,因此不能跳过 i 。而 [L, less)都是已处理的小于 p 的数,[less, i)都是已处理的等于 p 的数,所以在往左边交换的时候,i 是可以继续移动的。

解题思路:
-
归并排序


归并排序的递归调用逻辑比较简单,比较麻烦的是递归调用中的最后一步,合并两个有序数组的过程,实际上这里是对 nums 中的两部分有序区间 nums[L..mid] 和 nums[mid+1..R] 进行合并,因为并不存在真实的两个有序数组 nums1 和 nums2,但是合并的过程完全等价于合并两个有序数组。由于原始数组需要用来接收合并的结果,因此每次需要先将待合并的区间 [L, R] 拷贝到一个临时数组 temp 中,然后比较的时候是从这个 temp 数组中取较小的数字覆盖到原始数组的 [L, R] 区间。

628. 三个数的最大乘积

-
1. 排序
-
① 如果数组全是 非负数 ,则排序后 最大的三个数 相乘即为最大乘积;
-
② 如果数组全是 非正数 ,则 最大的三个数 相乘同样也为最大乘积。
-
③ 如果数组中有 正数 有 负数 ,则最大乘积既可能是 三个最大正数的乘积 ,也可能是 两个最小负数(即绝对值最大)与最大正数的乘积 。
-
综上,答案就是 max(最大的三个数乘积,最小的两个数与最大数乘积)


-
2. 线性扫描 ,找出最小的两个数和最大的三个数, 答案就是 max(最大的三个数乘积,最小的两个数与最大数乘积)



剑指 Offer 51. 数组中的逆序对 & 归并排序

-
1) 归并排序 , 可以在 合并两个有序数组 的过程中顺便统计 逆序对 的个数。 具体统计的时机是在比较两个数大小满足 nums[i] > nums[j] 时,区间 [i...mid] 的长度 mid - i + 1 就是逆序对的个数,我们不断累加这个值即可。


上面代码中的 count 也可以使用一个全局变量来统计,不需要相关方法中返回 count 值。
这个代码只是在归并排序的基础上加了一行统计代码,这里关键是要想清楚在什么条件下进行统计,我们知道归并排序过程中产生的两个有序区间在nums中是有先后顺序的,对于区间 [L...i...mid, mid+1...j...R] 由于 L...mid 有序,若 nums[i] > nums[j],则 nums[i..mid] 都大于 nums[j],并且此时 nums[i..mid] 都是位于 j 位置前面的,因此这时就符合了题目定义的逆序对要求。理解这一点很关键,否则即便知道归并排序怎么写,也不知道该如何统计。
解题思路:
-
2)归并排序,可以选择在两次子递归返回之后,在合并有序数组之前进行统计。

上面计算结果的for循环也可以这样写:
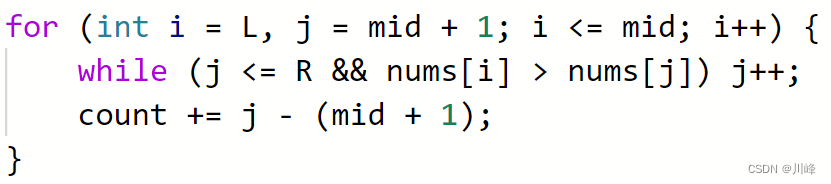
这两种计算方式的区别如下:

这道题目前在LeetCode上对应的题号是【LCR 170. 交易逆序对的总数】,发现很多剑指 Offer 的题目都被去掉了,以前搜到的现在搜不到了,也有可能没去掉只是题目被改了,但是解法没变。
493. 翻转对

-
归并排序 ,同剑指 51,在归并排序递归调用中,在两次子递归调用返回之后和合并两个有序数组之前,统计当前符合要求的翻转对的个数,再加上前面左右两次递归返回的个数作为当前递归返回的结果。
-
注意:这个题统计时机 只能在合并有序数组之前 ,在合并过程中无法正确统计。

上面计算翻转对的for循环也可以这样写:

315. 计算右侧小于当前元素的个数

-
1) 归并排序 , 将 原始元素 和其 下标 封装成一个对象 Info ,对 Info数组 进行 归并排序 的过程中计算答案。( 由于元素的下标在排序过程中也会发生变化,在更新答案时不知道设置给哪个下标,所以需要记住每个元素的原始下标,这样排序过程中就知道当前答案应该放入原来的哪个位置了 )
-
在每次递归调用中, 在两次子递归调用返回之后和merge合并之前 ,计算当前左右区间之间产生的符合要求的个数,答案放入数字对应的原始下标中。


注:也可以使用二维数组代替上面代码中的Info类。实现如下:

-
2) 归并排序 , 可以选择将统计的时机放在 merge有序数组的过程中 ,同样需要处理下标变化问题, 需要同时对元素和元素的下标索引数组进行归并排序。

上面代码中,统计时机主要有两种情况:
- ① 出现 nums[i] ≤ nums[j] 时,此时 [mid + 1, j) 区间的所有数都比 nums[i] 小
- ② 出现 j > R,即 j 越界时,此时 [mid + 1, R] 区间的所有数都比 nums[i] 小
参考下图理解:

327. 区间和的个数

-
1. 前缀和 + 暴力二重循序【超时】 , 先求前缀和,然后套两个for循环利用前缀和的差值求sum(i, j)符合[lower, upper]的个数

-
2. 前缀和 + 归并排序 ,先求前缀和,然后对 前缀和数组进行归并排序 ,每次递归返回归并排序过程中符合要求的区间和的个数,在两次子递归返回之后和 merge两个有序数组之前 ,进行统计这 两个有序数组之间可能 产生的区间和个数,最后再加上左右子递归返回之和作为当前递归返回结果。


上面代码中关键部分就是统计区间和个数的代码:

这里第一个 while 循环退出时,满足:prefixSum[j] - prefixSum[i] ≥ lower,第二个 while 循环退出时,满足:prefixSum[k] - prefixSum[i] > upper 且 prefixSum[k - 1] - prefixSum[i] ≤ upper,也就是说,此时 prefixSum[j...k-1] 区间的每一个数减去 prefixSum[i] 的差值都 ∈ [lower, upper],因此我们收集区间 [j...k-1] 的长度即此时针对 i 而言符合要求的区间和个数。
问题:为什么这里的 j 和 k 要写在for循环外面,不用每次都从 mid + 1 开始算呢?

如上图所示, 此时 [j, k - 1] 区间的值与 prefixSum[i] 的差值都在区间 [lower, upper] 内,而 j 前面的数减去 prefixSum[i] 差值都小于 lower,即 prefixSum[mid + 1...j - 1] - prefixSum[i] < lower,而下一轮循环 i 会移动到比当前更大的数 2,很显然,用prefixSum[mid + 1...j - 1]减去一个比之前更大的数得到的差值只会更小,之前就小于 lower,那现在就更小于 lower 了。所以下一轮循环中,j 和 k 只需要接着上次找到的位置继续和当前的 i 位置比较即可。

这样的好处是节省了很多无用的比较操作,提高了执行效率。如果 j 和 k 每次都从头 mid + 1 位置开始的话,会做很多无用功,比如上图中,如果 j 和 k 是从 8 开始与 2 进行比较,那么最终还是会得到跟现在相同的结果,但是相比之下 j 多比较了 [8-12]、k 多比较了 [8-17]。
理解这一点至关重要,本题如果将 int j = mid + 1, k = mid + 1; 放到for循环里面去,在LeetCode上提交会【超时】,但是放到for循环外面就很快(耗时大概几十ms)提交会通过。真所谓差之毫厘谬以千里。
归并排序类题目小结


-
1)递归函数是有返回值的, 左右递归的返回值 + 当前统计的返回值 ,作为当前递归的返回值。
-
2)此时, [L, mid] 和 [mid+1, R] 区间都是分别 有序 的。
-
3) i 遍历的初始值一定要从 L 开始,到 mid 结束, j 遍历的初始值一定要从 mid+1 开始,到 R 结束
-
4)由于 [L, mid] 和 [mid+1, R] 区间在原始数组是顺序排列的,即 [L...i...mid... mid+1...j...R] 所以 i 与 j 之间暗藏的一种的 下标顺序关系 是 i 永远小于 j ,也就是说所有的 i 都在所有的 j 前面
-
一种统计方法是外层遍历右边 [mid+1, R] 中的 j, 固定一个 j 后,内层到左边 [L, mid] 中循环的找满足某种关系的 i , 内层循环跳出时, [i...mid] 与 j 构成某种所求的关系。(一般是利用区间长度求个数)
-
另一种统计方法是外层遍历左边 [L, mid] 中的 i ,固定一个 i 后,内层到右边 [mid+1, R] 中循环的找满足某种关系的 j , 内层循环跳出时, [mid+1...j-1] 与 i 构成某种下所求的关系。(一般是利用区间长度求个数)
-
注意: i 和 j 都是 不走回头路 的,它们一直在前进,因此 初始化应该都放在外层 ,最好是 for 条件语句开始时。如果走回头路,可能会导致执行效率低。
-
必须满足比较关系是 单纯的 a 和 b 的大小比较,没有倍数关系 。
-
计算统计结果是发生在比较大小的 某个 if 条件 判断 中(可能是一个或多个)
75. 颜色分类

-
1. 单指针 + 两次遍历, 在 第一次 遍历中,将所有的 0 交换到数组的 头部 ,在 第二次 遍历中,将所有的 1 交换到头部的 0 之后 。此时,所有的 2 都出现在数组的 尾部 ,这样就完成了排序。
-
2. 双指针 + 两次遍历, 在 第一次 遍历中,将所有的 0 交换到数组的 头部 ,在 第二次 遍历中,将所有的 2 交换到数组的 尾部 。此时,所有的 1 都出现在数组的 中间 ,这样就完成了排序。
-
3. 三路快排的分区逻辑 ,把所有的 0 交换到数组的 前面 ,所有的 2 交换到数组的 后面 , 中间 剩下的都是 1 。跟方法2其实是一样的。
-
4. 计数排序 ,颜色作为下标,统计每种颜色出现了 n 次,然后分别按顺序输出每种颜色 n 次到 nums 数组中。




1365. 有多少小于当前数字的数字 & 计数排序

-
1. 计数排序 ,计数排序算法步骤:
-
① 对原数组进行 计数 统计
-
② 对计数数组自身求出 累加前缀和 ,
-
③ 倒序遍历原始数组的每个num输出到 count[num] - 1位置上
-
本题并不需要完成整个计数排序,因此到第②步就可以得到答案,我们遍历原数组的每个num,输出 count[num - 1] 到结果 res[i] 就是题目所求。
-
注意:这题能用计数排序的前提是题目元素范围是[0, 100],如果元素值的范围很大,是不能用计数排序的。


为什么 num 要放在 count[num] - 1 位置上呢?因为 count[num] 表示 ≤ num 的数量,例如 count[5] = 4,说明 ≤ 5 的有 4 个数,包括 5 在内,因此 5 应该放在这 4 个数中 index = 4 - 1 = 3 的位置。
我们拿到第②步的count前缀和累加数组就可以输出题目所求,因为 count[num] 是 ≤ num 的数量,题目所求的是 <num 的数量,所以只需用 num - 1 到 count 中取值即可。


-
2. 先排序 ,再统计,排序后的数组中,比 nums[i] 小的数字的个数就是排在它前面的数字的个数。
-
① 如果 无重复 数字,那么答案就是 i ,因为下标 i 正好表示它前面的区间 [0, i - 1] 的长度,例如 [ 7 3 6 5 2 1 9 ] -> [ 1 2 3 5 6 7 9 ] 小于 nums[ 4 ] = 6 的数字有 4 个。
-
② 如果 有重复 数字,应该 只取第一个重复数字的下标 i ,排除相同的数。例如 [ 3 8 1 8 2 8 4 8] -> [ 1 2 3 4 8 8 8 8 ] 后面 4 个重复的 8 应该只取 第一个 8 的下标 i 作为答案。
-
还有一个问题,最后输出答案的时候,我们不能直接遍历nums的每个数,将其排序后的下标保存到res[i]当中,因为排序后nums的下标改变了。为了解决这个问题,我们有两个方法:
-
1)可以使用一个Map预先记录原始数组的下标和对应的元素值,在后面输出答案的时候,从这个Map中取出元素的原始下标即可
-
2)或者我们可以更粗暴一点,直接把原始数组用一个新数组备份一下,后面输出答案时遍历这个备份数组里的元素。

这里统计排序后的每个数第一次出现时的下标使用的是一个数组型的map,这是因为本题的数据值范围不大只有[0, 100],当然你可以使用HashMap来做(数据值范围很大时只能使用HashMap)。
另外,这里使用temp数组备份了原始数组,以便最后输出答案时可以按照原始数组的顺序输出结果。当然,我还可以直接使用输出答案的 res 数组来作为备份数组,这样可以节省一个temp数组,代码如下:

164. 最大间距 & 基数排序 & 桶排序

-
1. 基数排序 O(n) ,先找 最大值 ,然后按照最大值的位数,对原数组的每个数按最大值的位数的每一位进行 计数排序 。
-
对数组进行基数排序完成后,遍历一遍数组,记录两两元素之间的最大差值即可。
-
注意点:计数排序在保存临时数组时,需要 倒序 保存。


基数排序算法的要求是数据元素可以分割成每一位来处理,且每一位的数据范围不大(如0~9),并且每一位的排序算法必须使用线性排序算法(如计数排序)。
-
2. 桶排序 O(n) , gap = (max - min) / (N - 1) 向上取整,将间距 小于 gap 的元素 放入下标为 bucketid = (num - min) / gap 的桶中。
-
每个桶内只维持 最大最小值 即可,无需桶内排序。
-
最终答案是桶与桶之间的最大间距。


-
1. 找到最大最小值max和min
-
2. 初始化桶数组buckets
-
3. 计算 gap = Math.ceil( (max - min) / (N-1) )
-
4. 遍历数组,计算当前元素对应的桶索引 bucketid = (num - min) / gap, 更新buckets[bucketid] 的最大最小值(与当前num比较)
-
5. 遍历桶数组buckets,计算桶与桶之间的最大间距:max(当前桶的最小值min - 上一个桶的最大值max) 。(跳过空桶)

本题应用桶排序的另一种思路如下:


这个代码跟前面一种的写法其实如出一辙,这里使用了 N + 1 个桶来存放 N 个数据,保证一定有一个空桶,空桶的存在只是为了保证最大差值不在桶内,只在桶与桶之间。但最关键的是 gap 值的计算,不管是分成 N 个桶还是 N + 1 个桶,gap 值都是用 (max - min) /(桶的个数 - 1)。这样用(num - min)/ gap 的计算方式来分配每个桶内的数字,能保证每个桶内的数字最大最小差值不会超过gap。
179. 最大数

-
1. 快排 ,这题关键是排序的判断标准,两个字符数字 x 和 y ,如果 (x 拼接 y) > (y 拼接 x) , 那么就 让 x 排到 y 的前面 ,否则就让 y 排到 x 的前面。如 x="34", y="12" ,因为 xy = "3412" 大于 yx = "1234"(字典序),所以 x 应排在 y 前面。
-
按照拼接后字符串的ASCII码大小排序即可,谁拼在前面组成的字符串的ASCII码大,谁就排在前面。
-
因为数字在ASCII码表中是有顺序的,所以利用 String.compareTo() 方法, 可以自然顺序的排序两个字符串,对于 a.compareTo(b) 如果大于0表示前者的字典序更大,小于0表示后者的字典序更大。



-
2. 使用 内置排序 算法,即调用 Arrays.sort() 方法,但是它的比较器只能 对 包装类型 进行排序,所以要转换一下。
-
在比较器的 compare() 方法中,如果 xy.compareTo.(yx) 大于 0 ,则 x 应排在前面, 返回 -1 ,否则返回 1 。

对于内置比较器的 compare(a,b) 方法,如果 a 排在前面应该返回一个负数,否则应该返回一个正数。所以上面代码中出现 x 排在前面的时候,返回 -1。这里也可以直接写成 return yx.compareTo(xy) 。
581. 最短无序连续子数组

-
1. 排序 ,将数组 nums 表示为三段子数组拼接的形式: numsA numsB numsC ,其中 numsA 和 numsC 有序, numsB 无序,题目要求最短的 numsB ,即找到最大的 numsA 和 numsC 。
-
因此我们可将原数组 nums 排序后 与原数组进行对比,从前面取最长的 numsA ,从后面取最长的 numsC ,就可以取到最短的 numsB 。
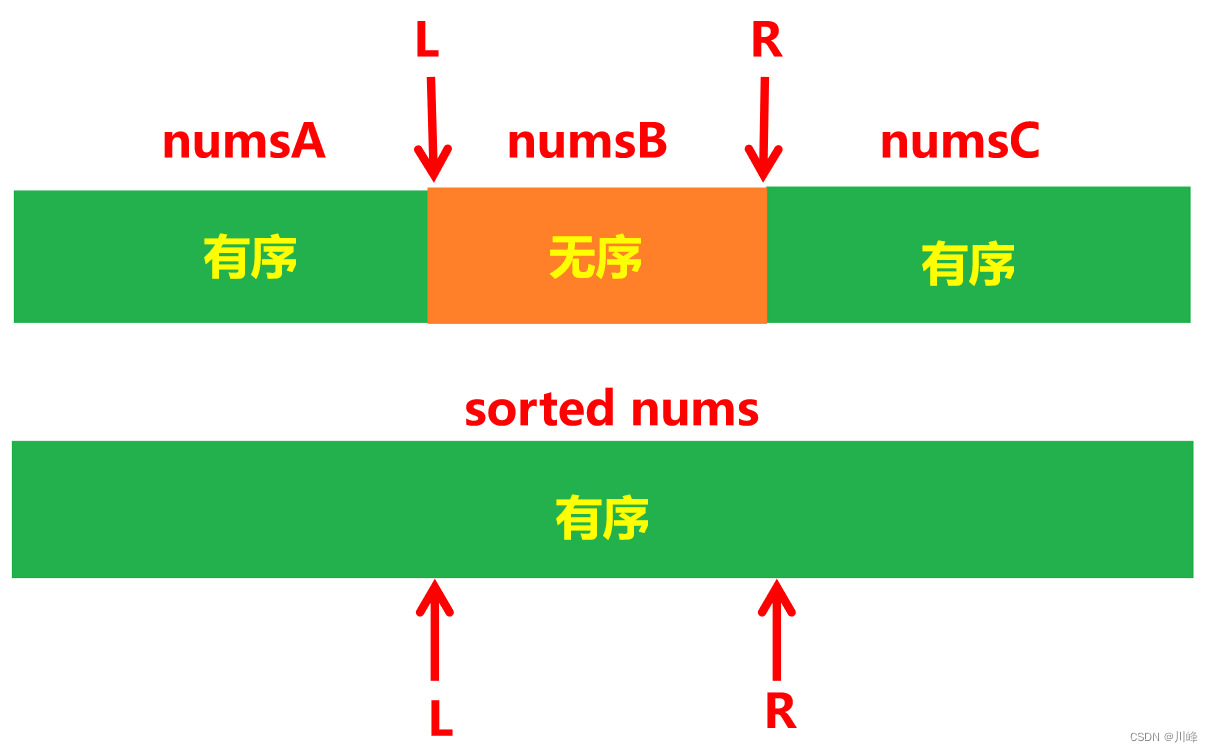

上面代码中省略的提前判断是否有序的代码可以这么写:

-
2. 双指针 ,在一遍循环中寻找无序段的 左边界 和 右边界 。
-
如果有序数组中间有一段逆序的: [1,2,3, 7,6,5,4 , 8,9,10]
-
从 左往右 更新 最大值 ,则肯定会出现 比最大值还要小的位置 ,记录 最后一个 位置即 右边界 ,
-
从 右往左 更新 最小值 ,则肯定会出现 比最小值还要大的位置 ,记录 最后一个 位置即 左边界 。


上面代码中的两个for循环也可以合并为一个for循环来做:

1470. 重新排列数组

-
1. 辅助数组 ,数组中每个 i 应该保存到结果数组的下标是:若 i 是前半部分即 i < n 则该去 2 * i 位置,否则应该去 2 * (i - n) + 1 位置。
-
注意:数组总共长度是偶数 2n 下标范围是 [0...2n-1] 。 x 范围是 [0...n-1] , y 范围是 [n...2n-1] 。


-
2. 辅助数组 ,结果数组中每插入一个 x 后面就紧跟着插入一个 y , x 范围是 [0...n-1] , y 范围是 [n...2n-1] 。
-
res 中按顺序每存入一个 nums[i] ,就接着存入一个 nums[n + i] 。
-
注意:数组总共长度是偶数 2n 下标范围是 [0...2n-1] 。


-
3. 借用二进制位 O(1)空间,由于题目数字的最大值是 1000 , 也就是最多只用到了 10个bit (2^10 - 1 = 1024 - 1 = 1023 > 1000) , 所以可以用每个数的 低10位 存储 原始数值 , 高10位 存储 重新排列到该位置的数字 。
-
我们可以使用每一个 nums[i] 的 最低 的 十个 bit ( 0-9 位),来存储原来 nums[i] 的数字; 再往前的 十个 bit ( 10-19 位),用来存储 重新排列后 正确的数字是什么。
-
最后再遍历一遍数组,将每个数的高 10 位右移到低 10 位上即可。

-
4. 置为负数 O(1)空间 , i 交换到该去的位置,并把该位置置为 负数 ,最后再遍历一遍置为 正数 。
-
注意:题目 nums[i] 均为 正数 ,所以可以使用这种方法。


这种方法虽然可行,但是有点绕,不如前面几种方法简单。
324. 摆动排序 II

-
快排 - 三路分区逻辑 ,
-
① 首先计算出 上中位数 的位置 mid = (N - 1) / 2 ,然后利用快排-三路分区逻辑按照中位数mid进行分区,分区的目标是使mid位于[less,great]区间。
-
分区完毕后,可以按照mid将原数组分成两个数组 A 和 B ,其中 A in [0, mid], B in [mid+1, N-1], A , B 不一定都有序,但是 A 中的数都 小于 B 中的数。
-
② 分别 倒序翻转 [0, mid] 和 [mid+1, N-1] 两个区间,然后 交叉插入 。
-
O(1) 空间的做法是利用整数 空闲的高位来存储插入的 数值, 低位 存储原始值。将每个元素的 低位 通过 或 运算保存到应该插入位置的数的 高位 上,最后再遍历一遍将所有数的 高位 右移到 低位 上。
-
O(n) 空间的做法是直接用额外数组接受倒序插入结果,完了再copy到原数组中。
我们可先写出主流程代码:

这里涉及到三个子函数,下面一个个来看。
首先第一个子函数是 middleSort ,也就是使用快排三路分区逻辑按照中位数进行分区,快排三路分区逻辑本质上是将原数组使用 2 个分区点分成了三个部分:[L, less) 部分都是小于分区点的值,[less, great] 部分都是等于分区点的值,(great, R] 部分都是大于分区点的值。按照mid进行三路分区的意思就是尝试使mid位于[less, great]这个区间,如果在一次分区之后发现不符合这个要求,就不断调整分区的左右边界 L 和 R 的值继续分区,直到满足这个条件为止。参考下图理解:
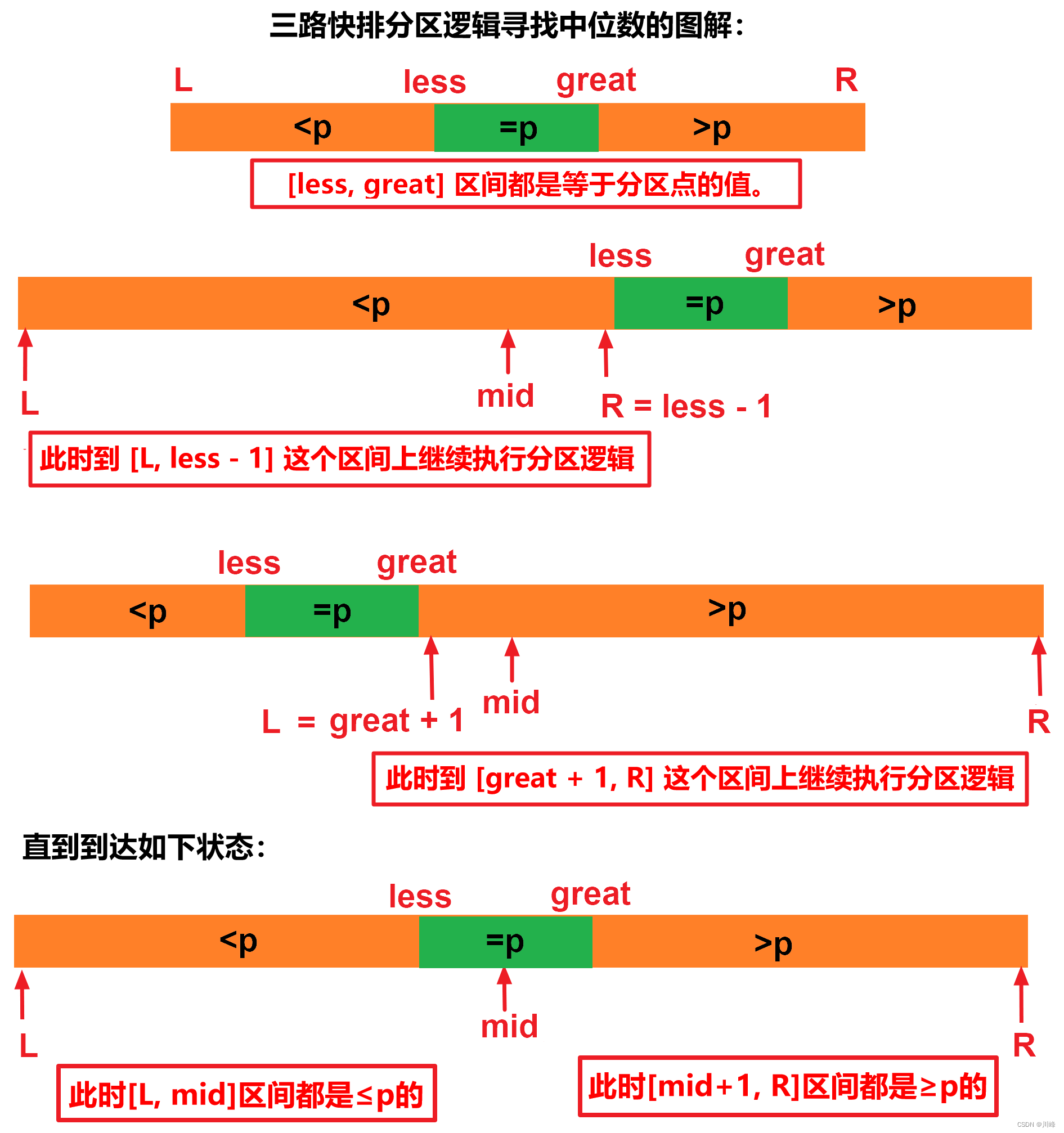
据此我们可以写出 middleSort 的实现代码:

下一个子函数是 reverse,也就是实现翻转数组,这个很简单,我们使用对撞指针就可以实现:

最后一个子函数是 shuffle,也就是实现交叉插入方法,我们可以直接参考1470题的代码,借用二进制位,在 O(1) 空间内完成 ,因为题目 nums[i] <= 5000, 也就是最多只用到了13个bit (2^13 - 1 = 8192 - 1 = 8191 > 5000),因此我们可以使用每一个数字的低13位来存储原始数字,使用高13位来存储重新排列到该位置的新数字。实现代码如下:

这里需要注意的是1470题的数组是长度为偶数的,但是本题并没有这个前提,所以这里需要分成数组长度是偶数和奇数两种情况来处理,偶数的情况与1470完全相同,奇数的情况,需要特别处理一个中间位置的数,它应该去到数组的末尾位置。

交叉插入方法:使用临时数组,O(N) 空间 参考1470

这里需要注意mid是取的上中位数,例如 [1,1,1,1,2,2,2] 总共 7 个元素,mid 是 index=3 的位置,在前面3个1和后面3个2依次存放完毕后,还剩余中间index=3位置的1,此时继续放入结果数组末尾,接下来就没有了,因此上面第二个保存的语句前面要加个if越界判断。
交叉插入方法:思路同上,借助空闲二进制位 O(1) 空间

1122. 数组的相对排序

-
1. 计数排序 ,先对 arr1 数组进行 计数 统计,然后按照遍历 arr2 的顺序将每个元素依次放入 arr1 中。
-
注意每个元素可能需要放入多次,此时根据 count 计数数组判断,只要某个元素在 count 中的数量 大于0 就循环不停地重复将其放入 arr1 中。
-
最后,将计数数组中剩余的计数大于0的下标按顺序放入 arr1 中即可,这些就是未在arr2中出现的数字 。(注意count数组中下标是数字,值是数量)
-
注意:题目中数组元素值范围在 [0, 1000] , 所以可以用计数数组来求。

-
2. 使用内置排序器 + 自定义排序规则 ,对 arr1 数组进行排序,排序规则是按照每个数 在 arr2 中出现的索引顺序进行排序。
-
具体比较器的规则:
-
1)如果两个数 a 和 b 都出现在 arr2 中,按它们的下标索引在 arr2 中出现的先后顺序排序 。
-
2)如果两个数 a 和 b 只有一个出现在 arr2 中,就让出现在 arr2 中的那个数排在另一个的前面 。
-
3)如果两个数 a 和 b 都两个都不在 arr2 中,按照原来的值升序排。
-
显然,如果想要知道 某个数 在 arr2 中的 下标 ,必须用一个 map 预先记录 arr2 中的 值 和 下标 的 对应关系。(本题可使用 数组型 的map)
-
注意:内置比较器只能对 包装类型 进行比较,因此需要先把 arr1 转成 Integer 型的数组,排序完最后再转换回去。

可见,这种方法虽然能够实现需求,但是比方法1计数排序要麻烦很多,比较器判断的条件很多,而且要数组要转换包装类型。





![[yolo系列:yolov7添加可变形卷积Deformable Conv V2]](https://img-blog.csdnimg.cn/36dd310d10e246bc81eb27d042fd943e.png)