一、题目描述与要求

判断是不是平衡二叉树_牛客题霸_牛客网 (nowcoder.com)

题目描述

输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。

在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树

平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

样例解释：

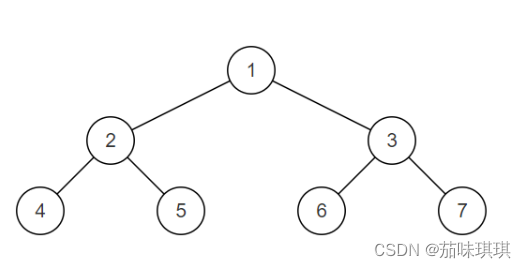
样例二叉树如图，为一颗平衡二叉树

注：我们约定空树是平衡二叉树。

数据范围：n≤100,树上节点的val值满足 0≤n≤1000

要求：空间复杂度O(1)，时间复杂度 O(n)

输入描述：

输入一棵二叉树的根节点

返回值描述：

输出一个布尔类型的值

示例

示例1：

输入：{1,2,3,4,5,6,7}

返回值：true

示例2：

输入：{}

返回值：true

---

二、解题思路

根据题目描述，我们需要去判断所给的二叉树是否为平衡二叉树；

平衡二叉树的性质为——它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

因而我们只需要去求出以每个结点为根结点时它的左右子树的深度，然后做减法，所有结点的左右子树结点深度差的绝对值不超过1，就代表只是一颗平衡二叉树，反之不是。

首先判断是否为一颗空树，是的话返回true；

递归求出左子树与右子树分别的深度，并进行判断；此外还要判断其左右子树是否也是一颗平衡二叉树。

---

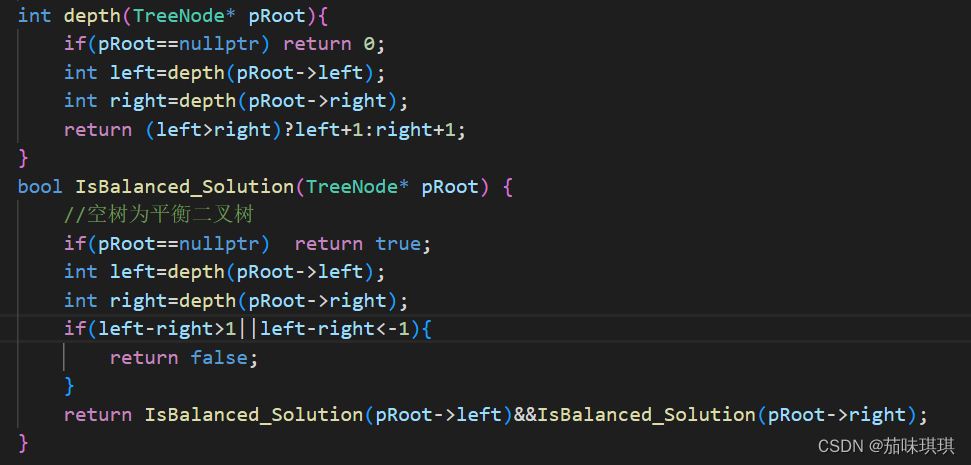
三、具体代码

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pRoot TreeNode类 
     * @return bool布尔型
     */
    int depth(TreeNode* pRoot){
        if(pRoot==nullptr) return 0;
        int left=depth(pRoot->left);
        int right=depth(pRoot->right);
        return (left>right)?left+1:right+1;
    }
    bool IsBalanced_Solution(TreeNode* pRoot) {
        //空树为平衡二叉树
        if(pRoot==nullptr)  return true;
        int left=depth(pRoot->left);
        int right=depth(pRoot->right);
        if(left-right>1||left-right<-1){
            return false;
        }
        return IsBalanced_Solution(pRoot->left)&&IsBalanced_Solution(pRoot->right);
    }
};