题目

给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第i个和第j个元素，如果满i<j且ali]>ali]，则其为一个逆序对;否则不是.

输入格式

第一行包含整数n，表示数列的长度。
第二行包含n个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

1 ≤n ≤100000

• 输入样例:

6
2 3 4 5 6 1

• 输出样例：

5

题解

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100010;

int n;
int q[N], tmp[N];

LL merge_sort(int l，int r)
{
	if (l >= r) return 0;
	int mid = l +r >>1;
	LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);

	//归并的过程
	int k = 0, i = l,j = mid + 1;
	while (i <= mid &&j <= r)
		if(a[i] <= q[j) tmp[k ++ ] = q[i ++ ];
		else
		{
			tmp[k ++] = q[j ++ ];
			res += mid - i + 1;
		}
	//扫尾
	while (i <= mid) tmp[k ++] = q[i ++ ];
	while (j <= r) tmp[k +] = q[j ++ ];

	//物归原主
	for (int i = l，j = 0; i <= r; i ++，j ++)q[i]=tmp[j];
	
	return res;
}	
int main()
{
	cin >> n;
	for ( int i = 0; i < n; i ++ ) cin >>q[i];
	cout << merge_sort(e，n - 1) << endl;
	return 0;
}

思路

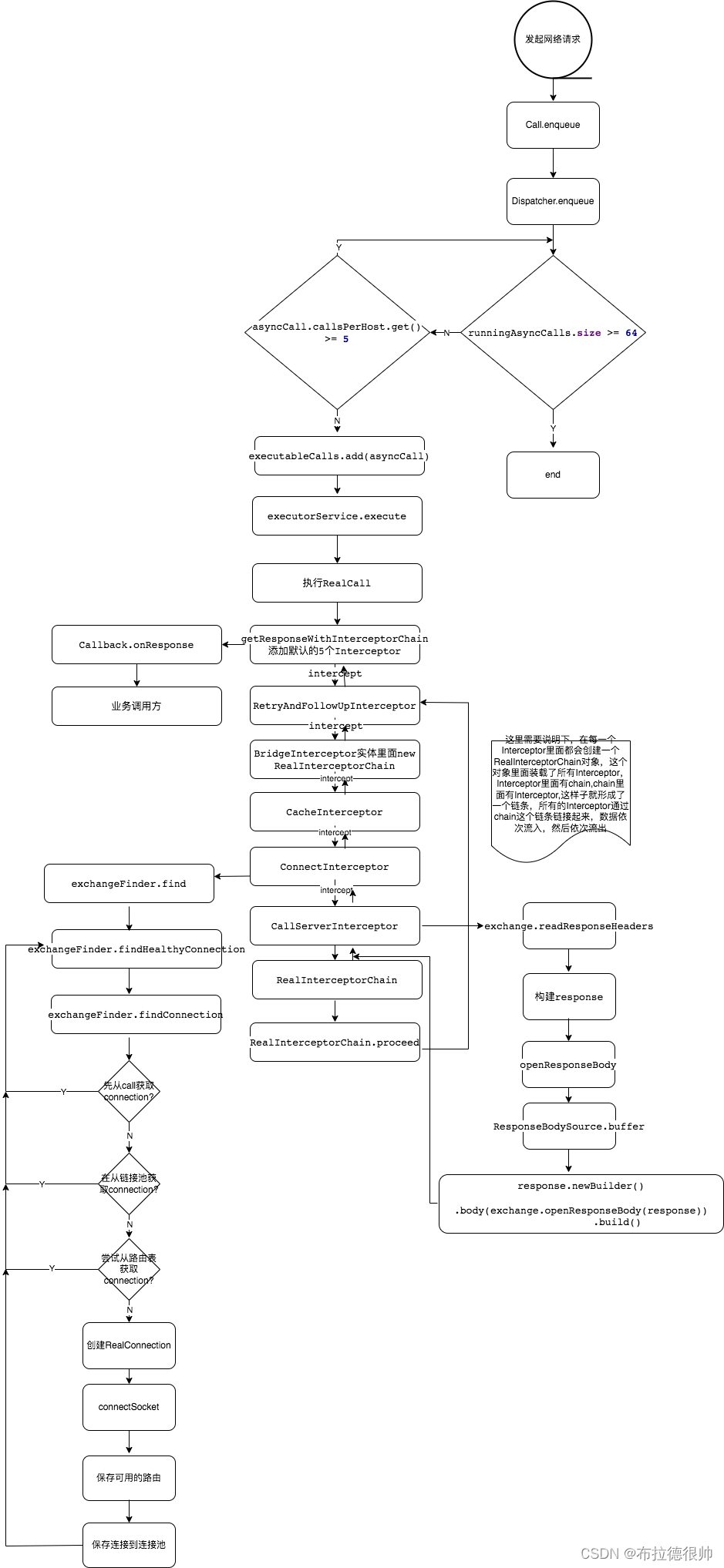
稍微改动归并排序，在归并排序中返回三种情况的数量，哪三种，如下图。

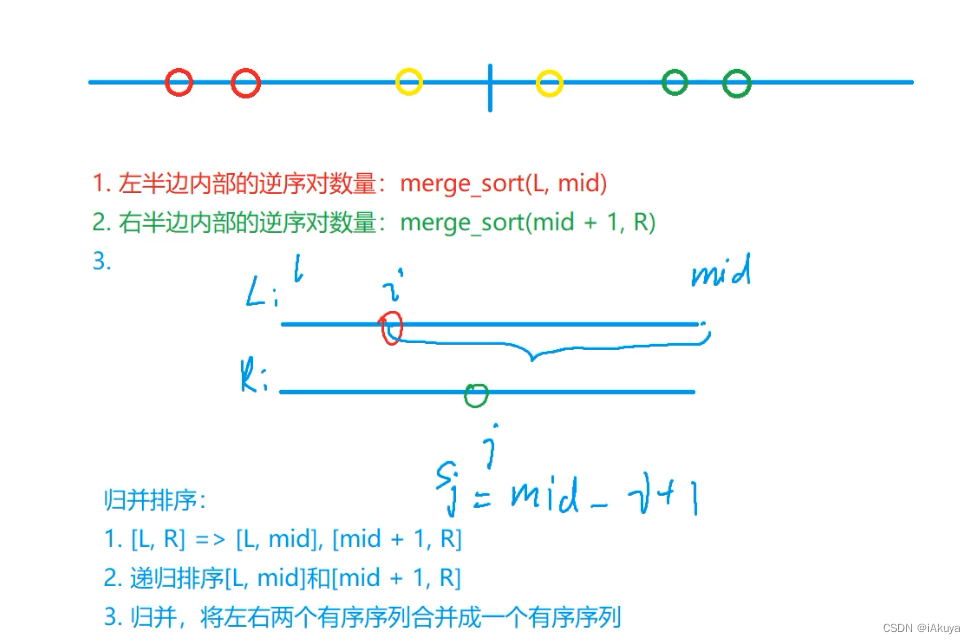
注意爆int