概述
- 输入的特点
- 是一个向量序列
- 序列的长度是可变的
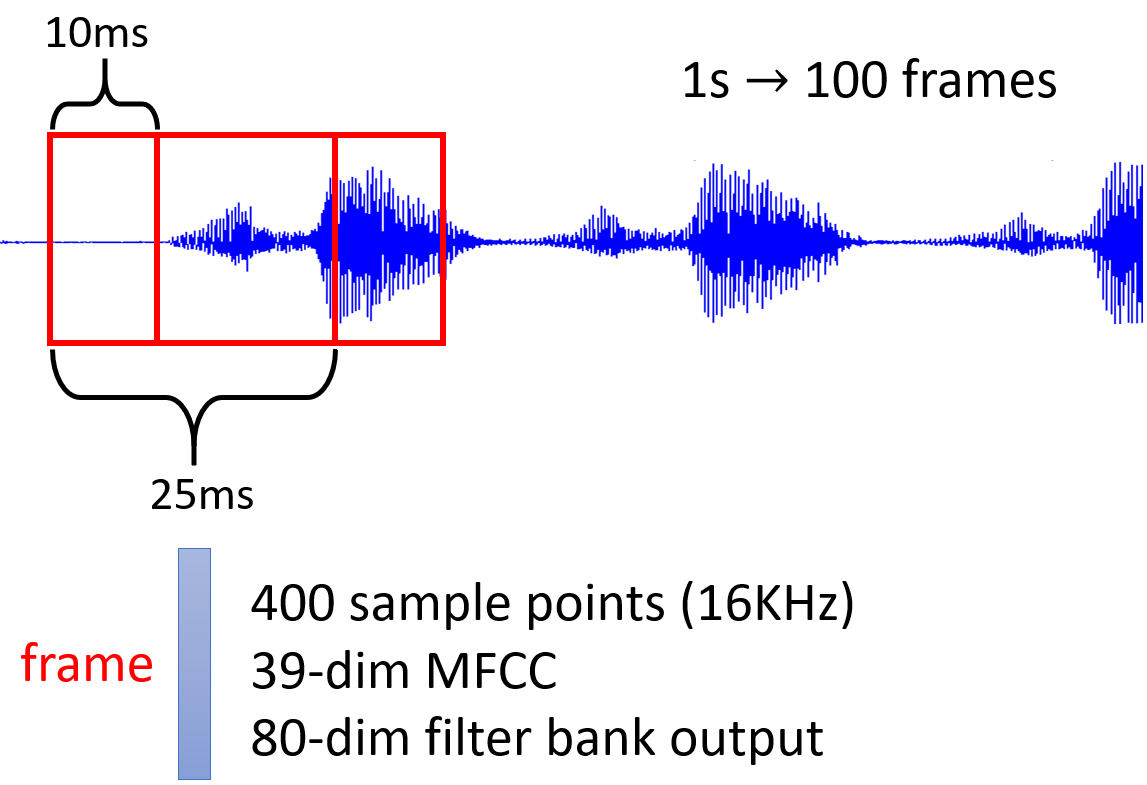
- 例如:对于音频数据,STFT之后,得到每个帧的特征,这些帧在时间维度上构成序列
- 输出类型有三种
- 对序列中的每一个向量,都有一个对应的输出,比如说要对一段文本里的每个词,都判断词性。此时输出序列和输入序列长度相同
- 只需要输出一个向量,比如说话人识别、音频事件分类
- 输出序列的长度不能确定,比如语音识别、机器翻译
接下来专注于介绍第一种输出类型,这种任务通常被称为序列标注(Sequence Labeling)
动机
- 假设输入一个句子,且每个词已经向量化,需要输出每个词的词性(名词、动词、形容词等),此时网络输出就是,当前输入属于每种词性的概率
- 如果每个词都独立地输入到网络,即无论词的顺序如何变化,只要输入的元素不变,对应的输出元素就不变,此时用MLP即可完成该任务

- 但是,对于同一个词,在句子中的位置不同,其词性也会发生变化。网络需要获取上下文信息,才能使同一个元素,在不同的输入位置,对应不同的输出。要做到这一点,可以将输入元素及其邻近元素,集成到一个窗口中,把窗口作为输入序列的元素

- 以窗口作为输入,网络获取上下文信息能力是有限的,如果希望考虑整个输入序列的信息,该怎么做呢?可以把窗口开大一点,但是输入序列的长度是可变的,因此无法采用固定大小的窗口,实现全序列信息捕获
- 引入Self-attention模块,效果是:使序列中的每个元素都获取全序列的上下文信息,并且序列长度不变。将Self-attention处理后的序列,再输入到MLP,其分类结果,就包含了全序列的信息
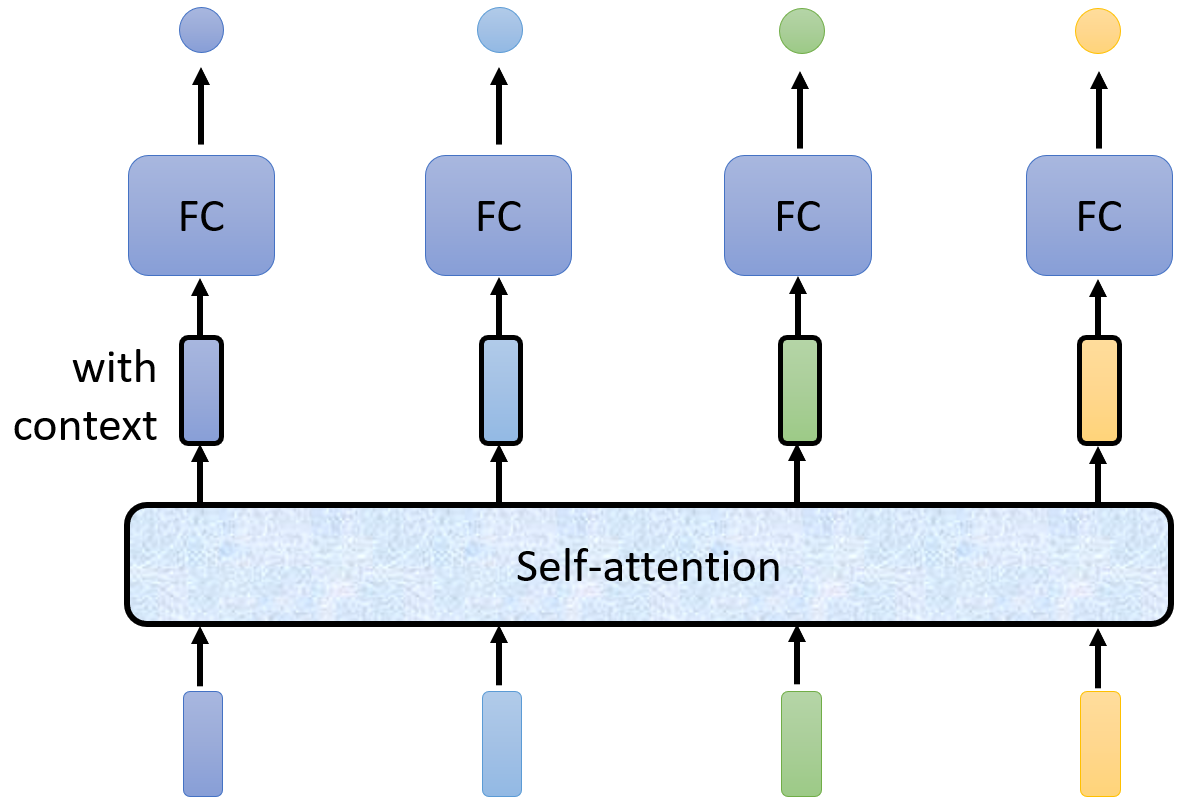
- 在上图的结构中,Self-attention用于捕获全序列信息,MLP用于集中该位置的信息,因此可以交替使用
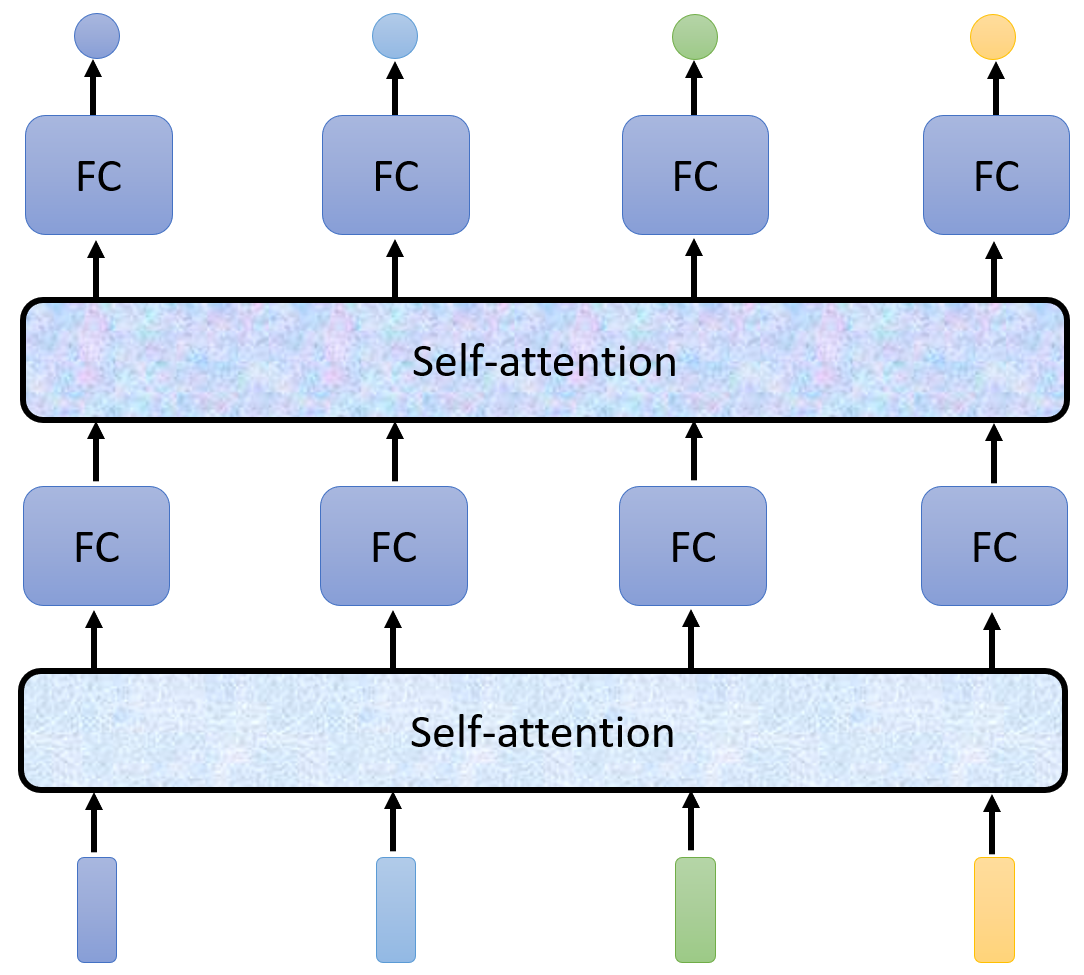
数学过程
- 现在专注于Self-attention内部,要得到某一位置的输出,首先要在输入序列中找出与当前位置最为关联的其他位置的向量,具体做法是:将当前向量与其他向量两两组合,计算相关性,用
α
\alpha
α表示
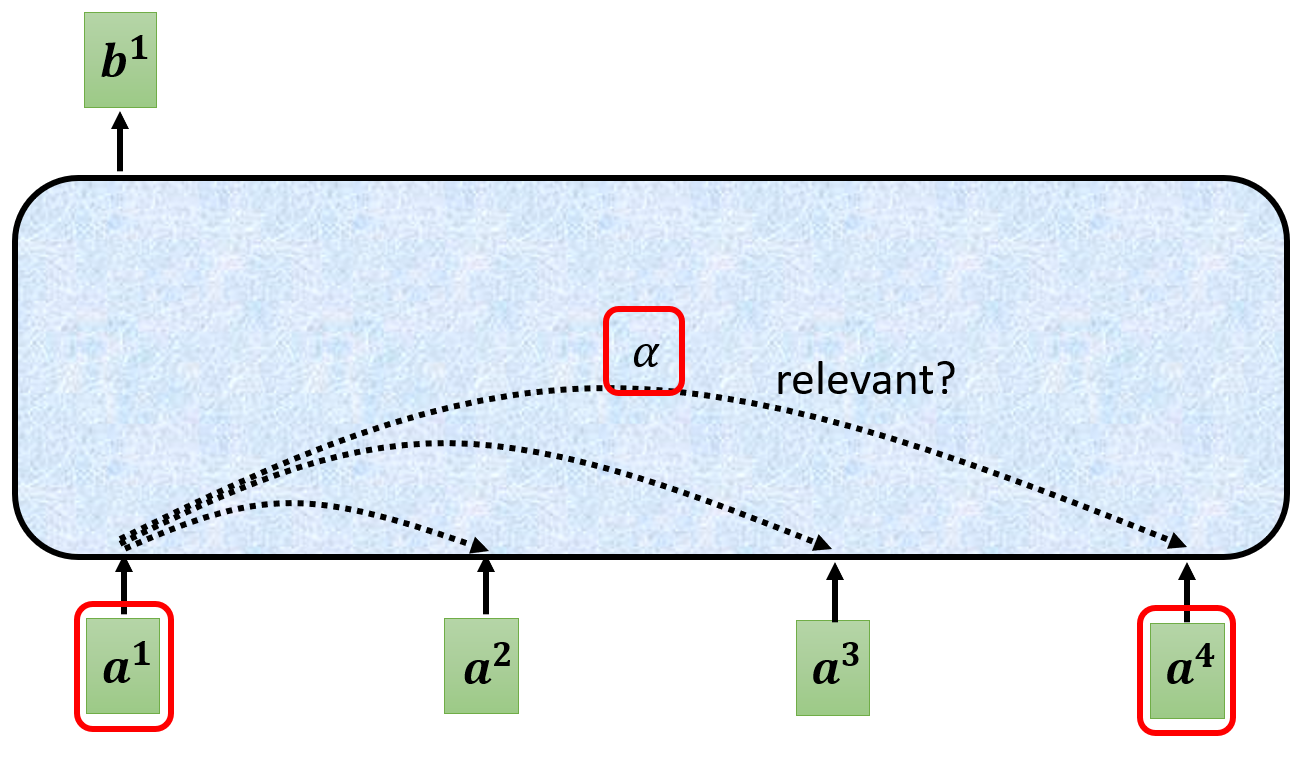
- 计算相关性的方法:
- Dot-product:q和k对应项相乘再相加,得到一个标量
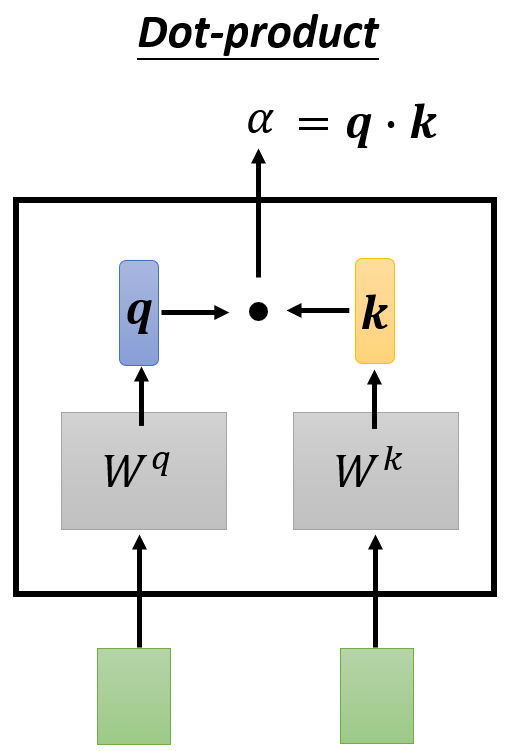
- Additive:+号表示q和k对应项相加,最后输出也是标量
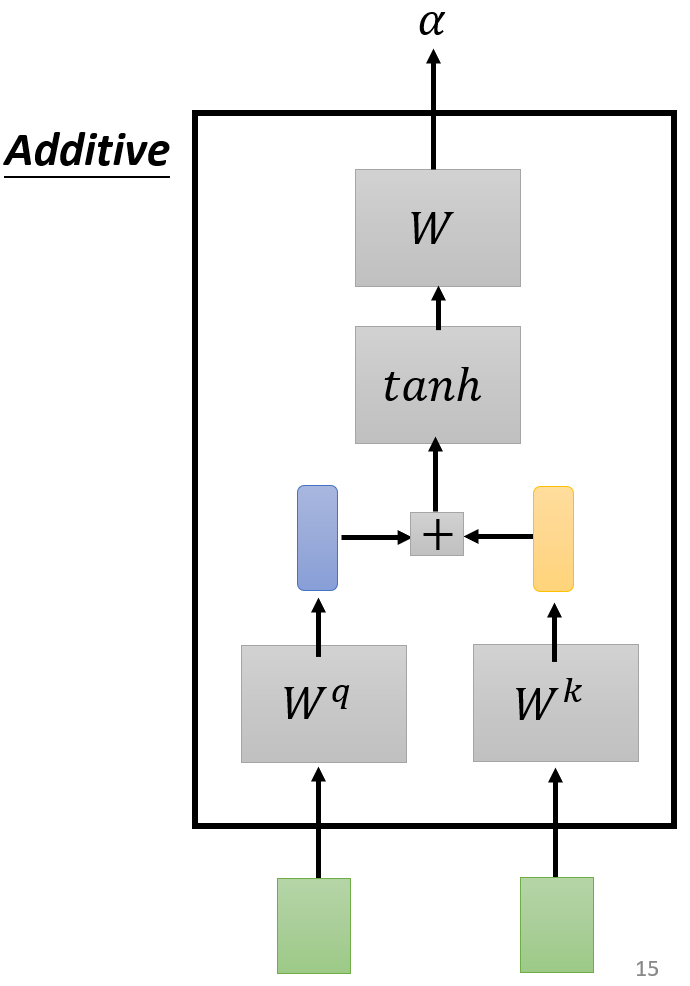
- Dot-product:q和k对应项相乘再相加,得到一个标量
其中,Dot-product是最为常用的方法,下面的介绍也采用这种方法
-
将当前向量与其他向量两两组合,计算相关性:对当前向量求query,对其他向量分别求key,可以理解为将当前向量和其他向量都映射到另一个空间,在新的空间中求相关性,相关性计算的结果称为Attention分数
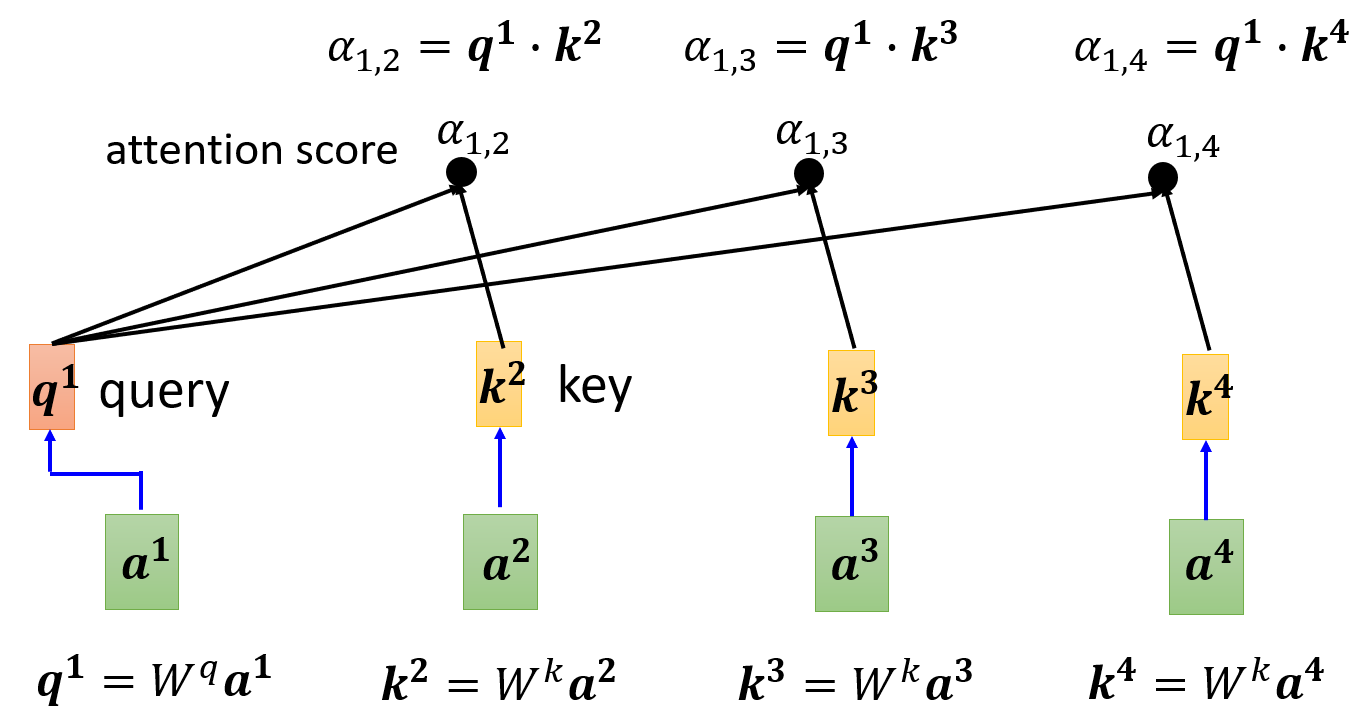
-
注意,在实际使用中,还会让当前向量和自身(Self)也计算Attention分数。得到的各位置的 α \alpha α后,还需要对 α \alpha α进行伸缩(scale),即除以 D \sqrt{D} D,D是 a i a^i ai的向量维度。要除以 D \sqrt{D} D的原因是:
- 在向量维度升高时,Dot-product的输出方差很大,会出现过大的值,输入Softmax之后,会导致梯度消失,堆叠多层Self-attention时,这个情况尤为明显
- 输出各类别概率的Softmax,则不需要对输入进行scale,因为靠近监督信号,如果类别正确,则参数不需要较大更新,若类别错误,则整体tidings接近1,需要参数较大的更新
-
然后经过Softmax才是最终的分数,Softmax本质上是max函数的软化(可微分)版本,特点是:
- 输入输出维度相同
- 输出为概率分布,每一项都是正数,每一项求和等于1
- “赢者通吃”,输入中最大的值输出会很接近1,其他的值输出会很接近0
- 是max函数的可微分版本
-
Softmax使得与当前向量最相关的向量,对应的Attention分数最接近1。Softmax并不是唯一选择,使用ReLU也可
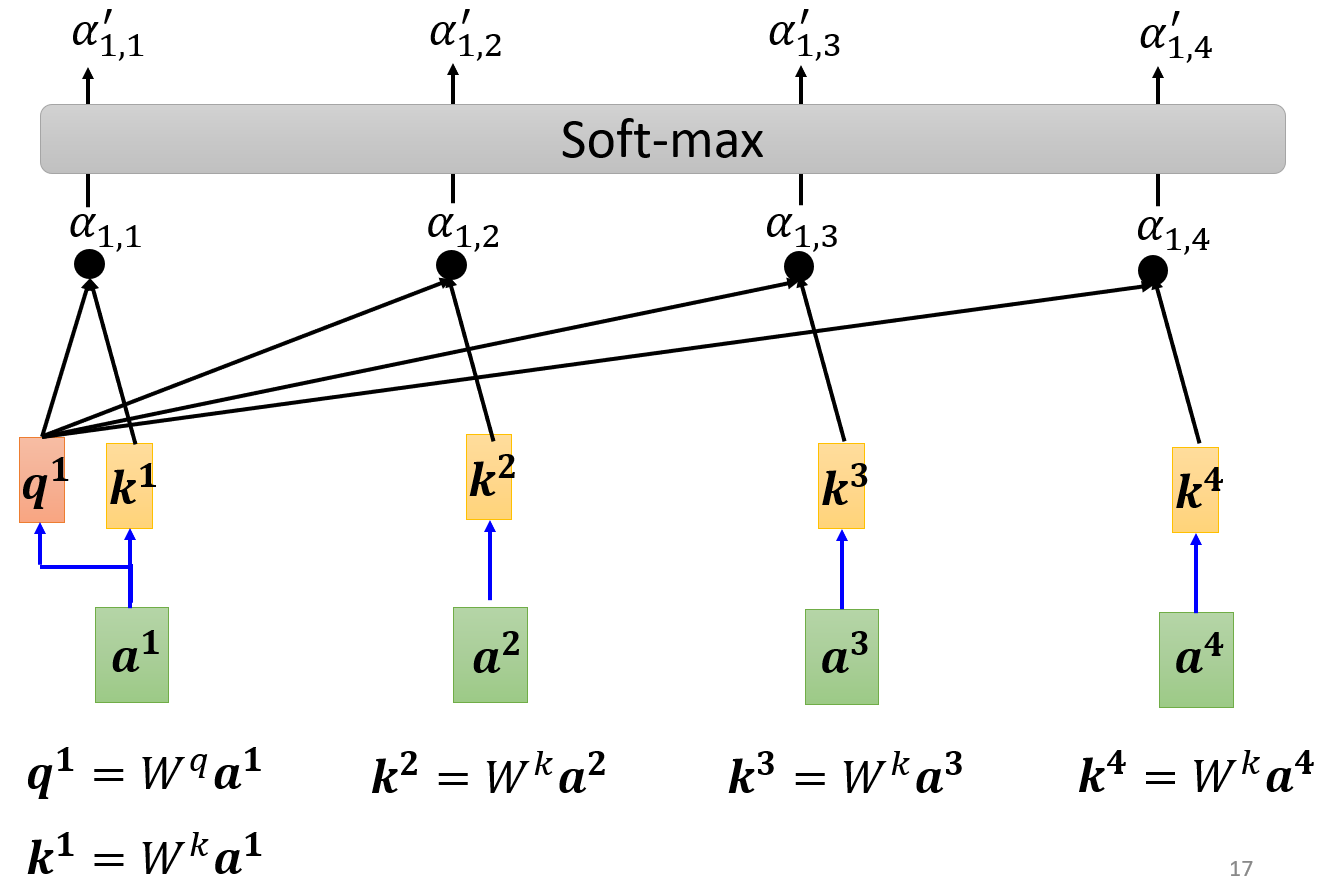
-
下一步是根据Attention分数,对每个向量,提取需要的信息value,注意对自身也需要提取value,公式如下,实际上是对value加权求和,得到一个向量,图中的 × \times ×表示向量的数乘
b 1 = ∑ i α 1 , i ′ v i b^1 = \sum_{i} \alpha'_{1,i} v^i b1=i∑α1,i′vi
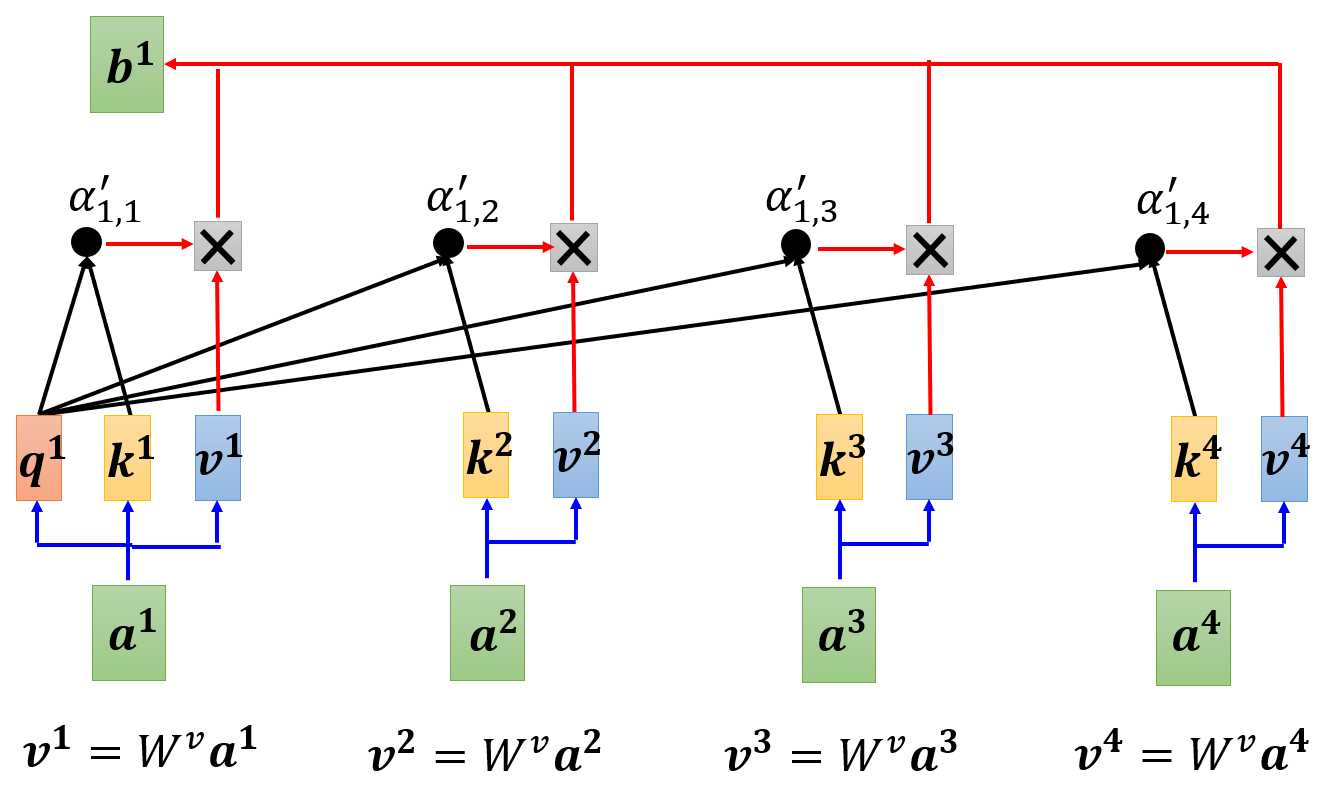
-
上述过程中,所有的W都是矩阵,因为矩阵和向量的相乘会得到向量,所以,所有的q、k、v都是向量
-
实际中,为了运算效率,常常会以矩阵形式运算,也就是说,将每个位置向量 a a a,视作列向量,然后在行的方向上串联(concatenate)起来,得到矩阵 I I I, W W W与 I I I相乘会得到矩阵,比如: W q W^q Wq与 I I I相乘,会得到矩阵 Q Q Q, Q Q Q表示:将每个位置向量对应的 q q q,视作列向量,然后在行的方向上串联起来。同理,也可得到矩阵 K K K和 V V V
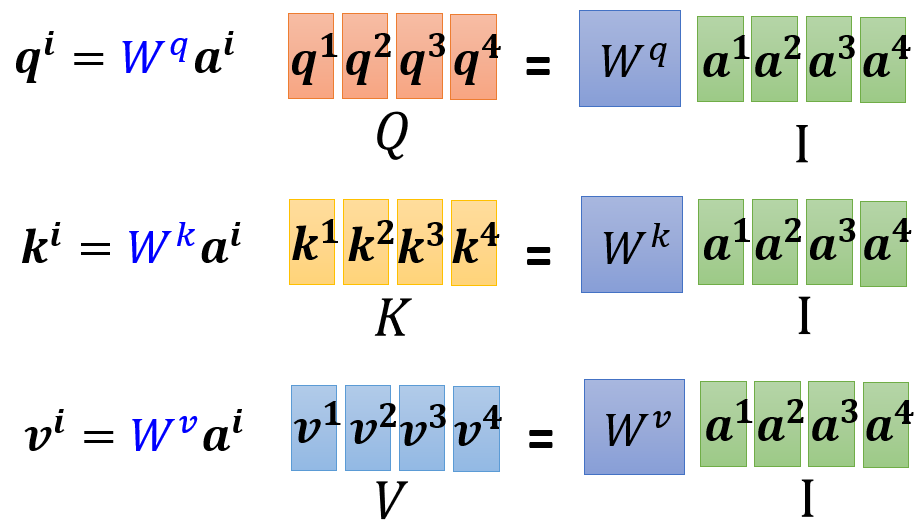
-
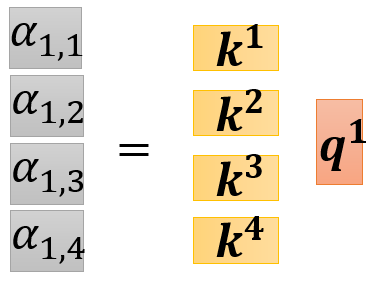
得到 Q Q Q、 K K K、 V V V后,需要计算Attention分数,每个位置的Attention分数都是标量,位置i对其他位置(包括位置i本身)的Attention运算,可以用 K K K的转置与 q i q^i qi相乘得到,得到的Attention分数是列向量
-
计算Attention分数的过程进一步矩阵化:将每个位置的Attention分数列向量,在行的方向上串联起来,得到的矩阵称为 A A A,可以用 K K K的转置与 Q Q Q相乘得到。之后再对 A A A的每一列先进行scale,再计算Softmax(ReLU也可)就得到最终的Attention分数矩阵 A ′ A' A′

-
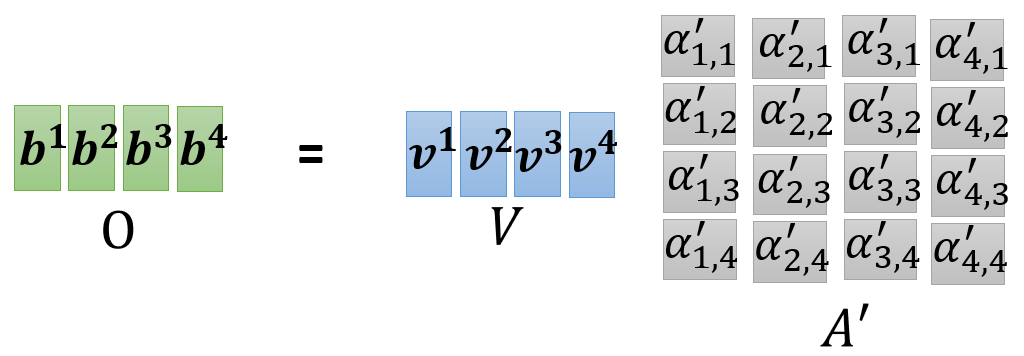
得到 A ′ A' A′之后就可以计算value了,因为 V V V是每个位置的value列向量在行方向上串联形成的, A ′ A' A′的每一列就是每个位置的Attention分数列向量,又因为矩阵相乘就是前一个矩阵的行,乘以后一个矩阵的列,因此 V V V和 A ′ A' A′相乘,即可得到每个位置的value列向量在行方向上的串联,结果记为 O O O
-
矩阵运算总结如下,其中,只有 W q 、 W k 、 W v W^q、W^k、W^v Wq、Wk、Wv是需要学习的参数
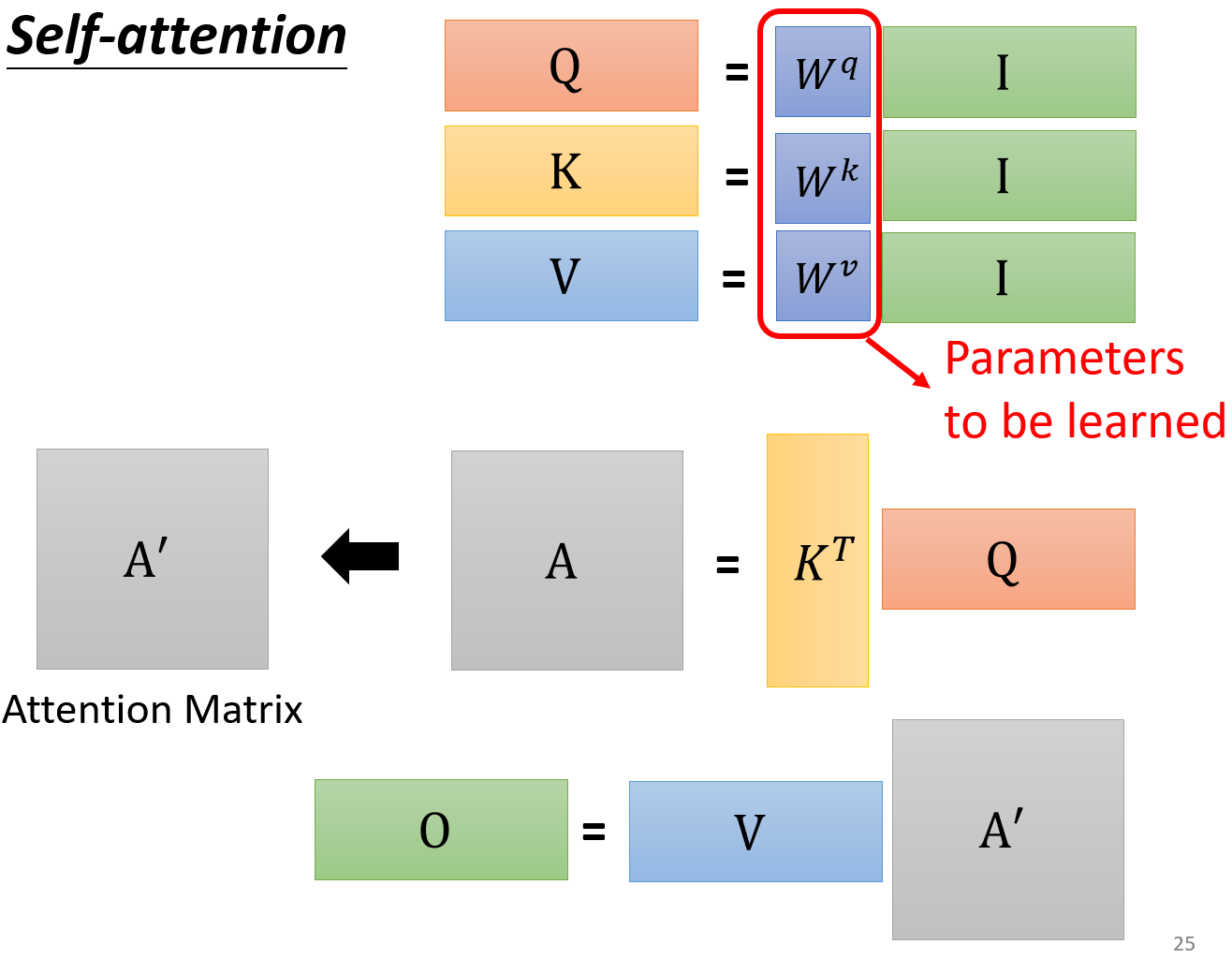
Multi-head Self-attention
- 为什么需要Multi-head Self-attention(多头自注意力)呢?因为在计算相关性的步骤中,相关性这一概念可以有多种解释,如果把q向量映射到更多的空间中,网络就能学习多种相关性
- 以2个head为例,得到位置i的
q
i
q^i
qi向量后,再引入两个矩阵
W
q
,
1
、
W
q
,
2
W^{q,1}、W^{q,2}
Wq,1、Wq,2,计算对应的多头q向量:
q i , 1 = W q , 1 q i q i , 2 = W q , 2 q i \begin{aligned} q^{i,1}&=W^{q,1}q^i \\ q^{i,2}&=W^{q,2}q^i \end{aligned} qi,1qi,2=Wq,1qi=Wq,2qi
同理也可得到 k i 、 v i k^i、v^i ki、vi向量的多头映射
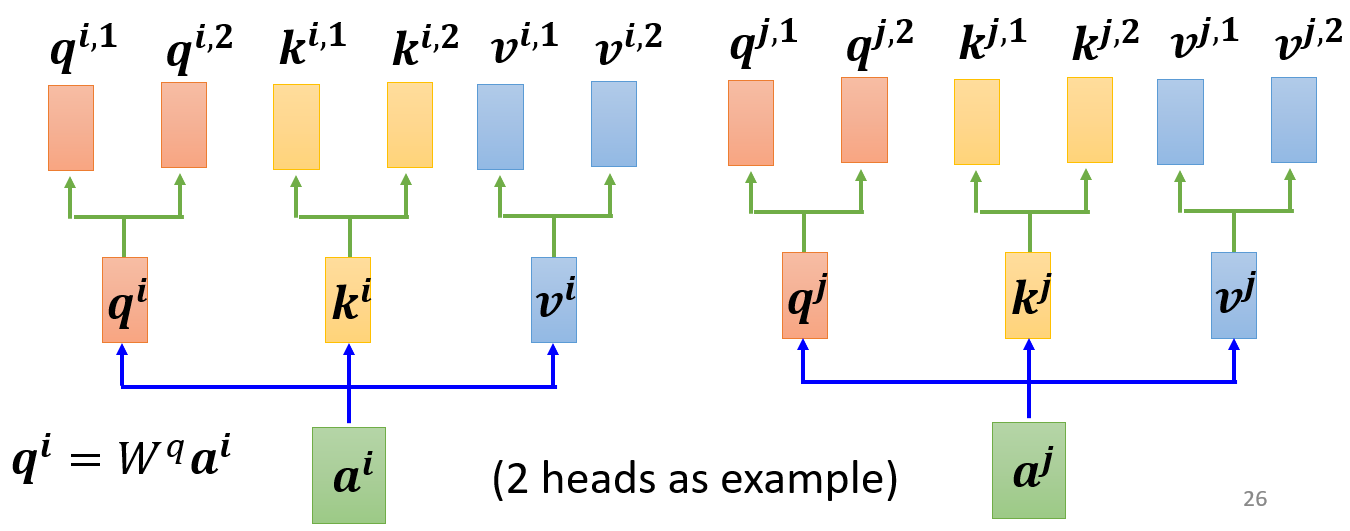
- 得到多头的q、k、v向量后,属于同一个头的q、k向量单独计算Attention分数,再对属于同一个头的v向量加权求和,得到当前头的输出。对每个头都进行该操作,就得到多头的输出
b
i
,
1
、
b
i
,
2
b^{i,1}、b^{i,2}
bi,1、bi,2
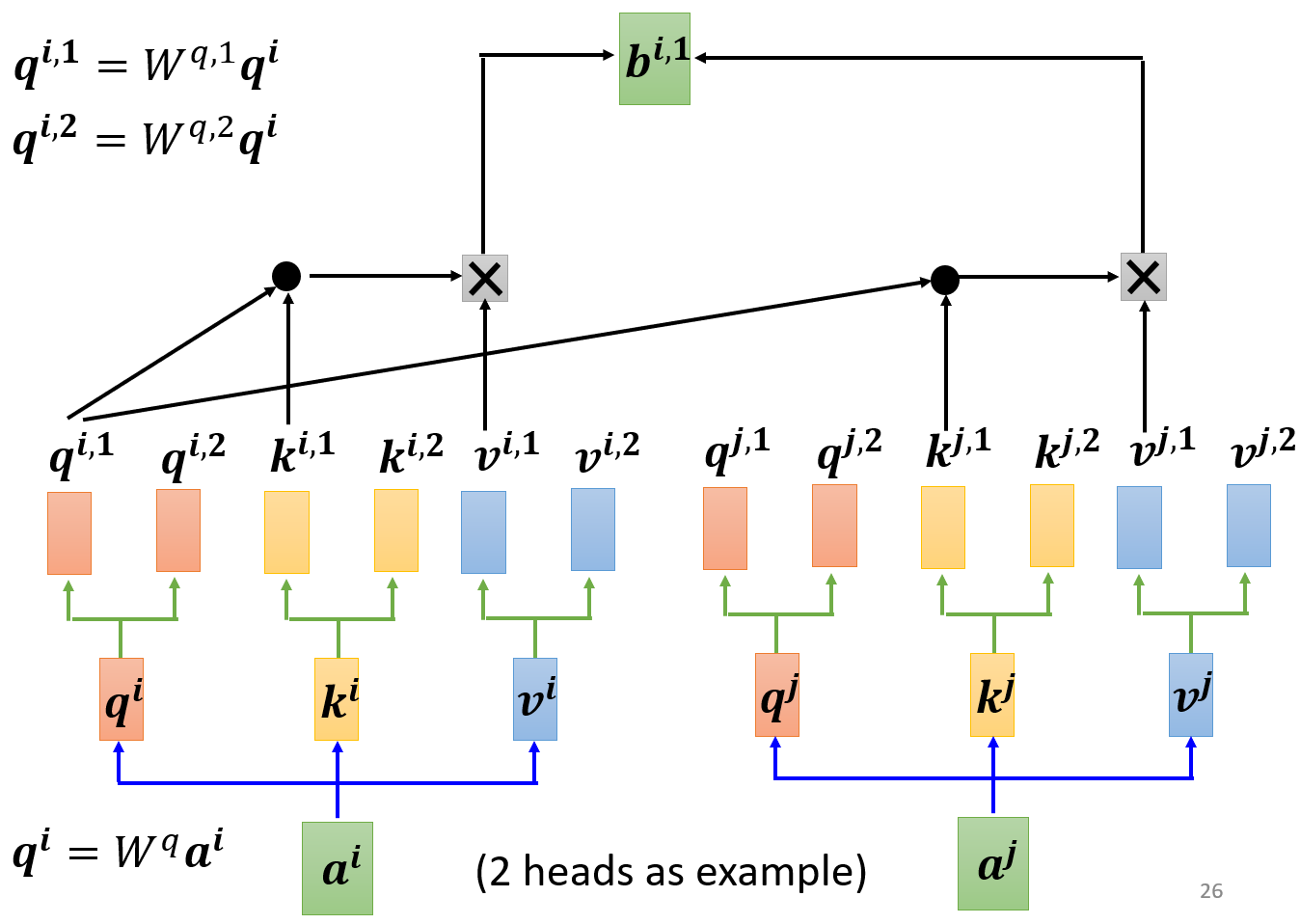
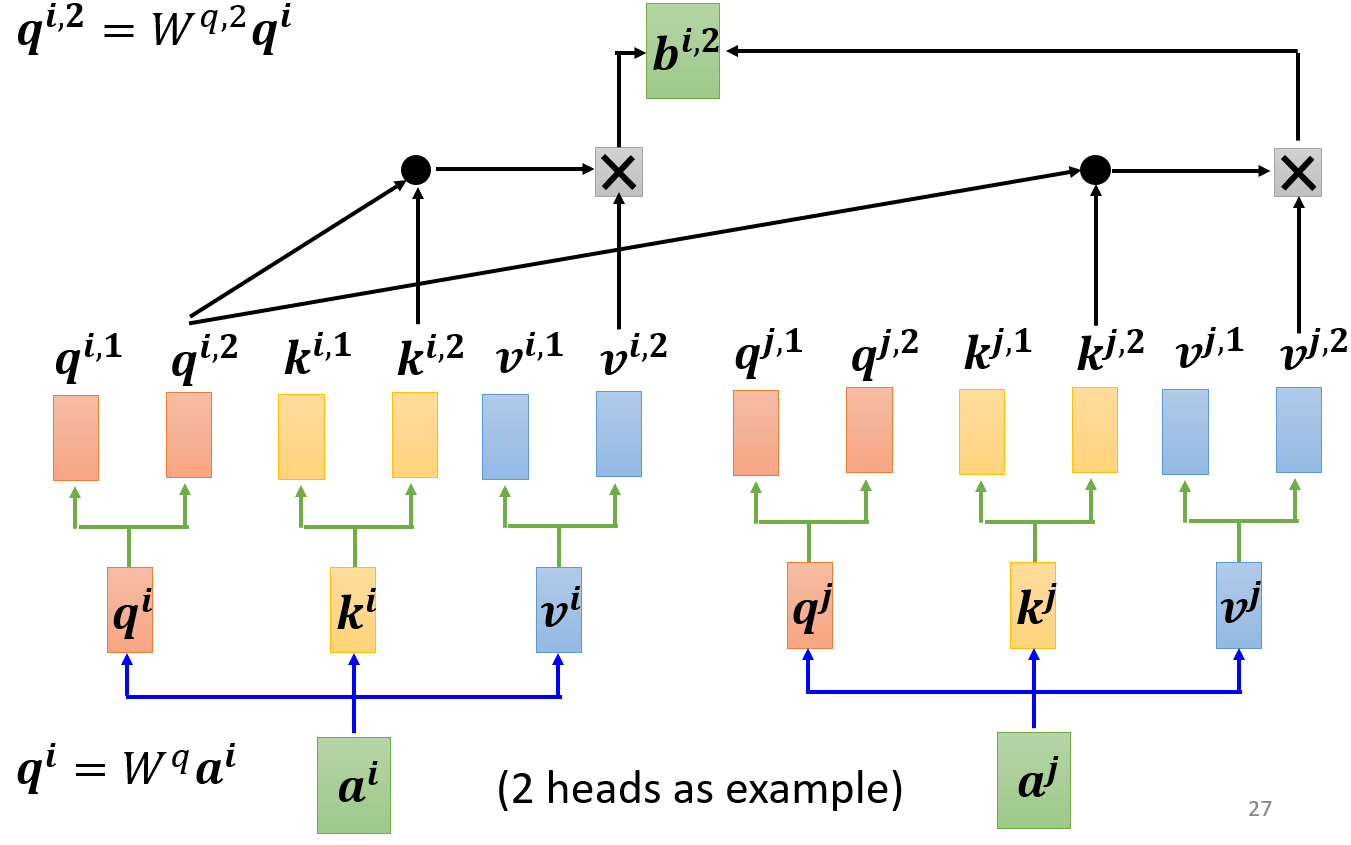
- 将多头的输出在列方向上串联起来,经过
W
o
W^o
Wo,投射成一个列向量,这就是Multi-head Self-attention的最终输出

Positional Encoding
- 最开始我们假设:输入一个句子,且每个词已经向量化,需要输出每个词的词性(名词、动词、形容词等)。这里的词向量化实际上并没有包含每个词在句子中的位置信息,上图中的输入 a 1 、 a 2 、 a 3 、 a 4 a^1、a^2、a^3、a^4 a1、a2、a3、a4的序号上标,是为了便于理解,假如输入顺序变化成 a 1 、 a 3 、 a 4 、 a 2 a^1、a^3、a^4、a^2 a1、a3、a4、a2,Self-attention对应的输出内容也不会变化,只是顺序随之变化而已(即输出的每个列向量的值不会变,只是列向量以不同的顺序,在行的方向上串联)
- 所谓位置信息,在本任务中是指句子中单词的相对距离,这对于词性标注而言是有用的,例如:形容词后常跟名词,动词后常跟名词,代词常在句首等。
- 位置编码,具体而言是对输入向量的不同位置,都进行独一无二的编码,记为 e i e^i ei,将 e i + a i e^i+a^i ei+ai作为位置编码后的输出,然后再输入到Self-attention
- 位置编码函数可以是人工设计的一个离散函数,也可以是可学习的参数,位置编码的最优方式目前尚未有定论
- 位置编码函数记为
f
P
E
(
⋅
,
⋅
)
f_{PE}(\cdot,\cdot)
fPE(⋅,⋅),输出是一个向量,输入两个参数,第一个参数是当前向量的位置序号,第二个参数是一个向量,输出向量的维度,与第二个参数的维度相同。常用的一个位置编码函数:
f P E ( i , 2 j ) = sin i 1000 0 2 j / D f P E ( i , 2 j + 1 ) = cos i 1000 0 2 j / D f_{PE}(i,2j)=\sin \frac{i}{10000^{2j/D}} \\ f_{PE}(i,2j+1)=\cos \frac{i}{10000^{2j/D}} fPE(i,2j)=sin100002j/DifPE(i,2j+1)=cos100002j/Di
其中, D D D是 a i a^i ai的向量维度,由于这个函数区分奇偶,所以要迭代地调用 f P E ( ⋅ , ⋅ ) f_{PE}(\cdot,\cdot) fPE(⋅,⋅)才能得到一个向量,第二个参数也变成了当前维度的序号
Self-attention VS CNN
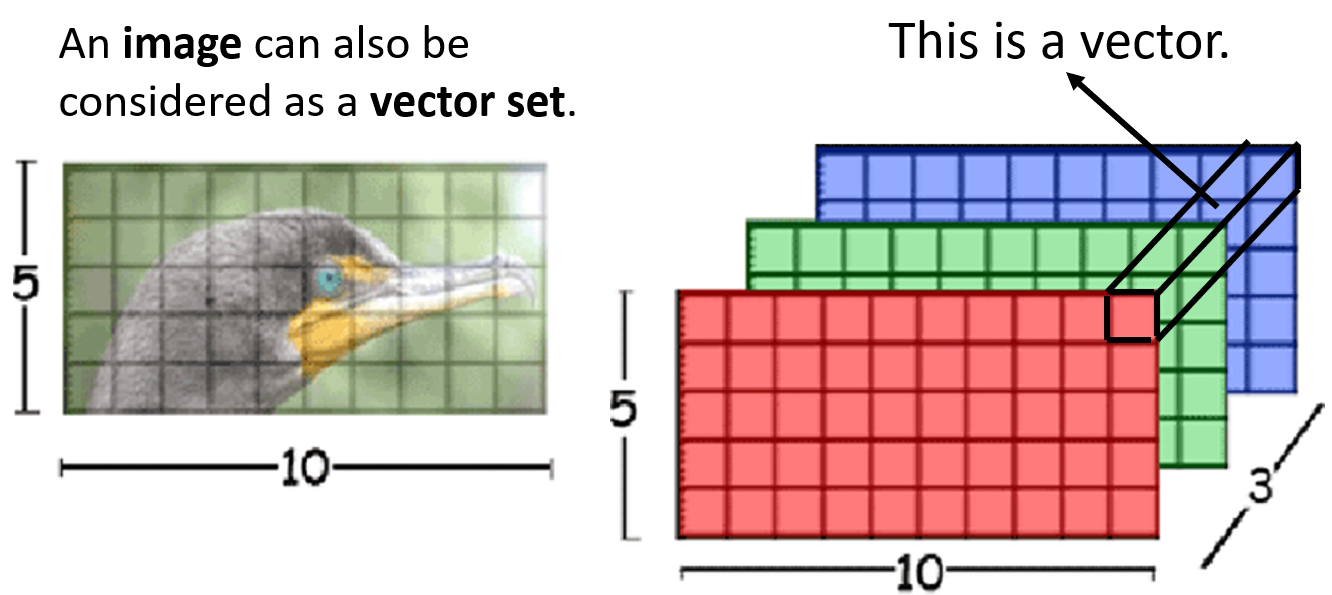
- Self-attention的输入是向量序列,那么图像可否被视作向量序列呢?有一种角度是将图像上的每一个像素点视作一个向量,图像的通道数就是向量的长度,分辨率的值就是序列的长度。但这样处理,神经网络的参数量将会巨大,所以用于图像处理的Self-Attention都会先将图像分块,将每个图像块向量化,再进行Self-Attention运算,有一句名言“An Image is Worth 16x16 Words”
- 那么,常用于处理图像的神经网络CNN,与用于处理向量序列的Self-attention有何异同呢?
- 假如当前向量是图像上的一个像素点,Self-attention在计算相关性时,是对整张图像的每一个像素点都计算相关性,而不仅仅是该像素点的邻域;而CNN的每一个卷积核,在对每个像素点运算时,只考虑了该像素点的邻域
- 因此,CNN可以视作是一种简化版的Self-attention,每个卷积核在运算时,只考虑了特征图上每个像素点的邻域,随着CNN深度加深,邻域对应原图中比较大的区域,因此,感受野逐渐增大的CNN是在逐渐接近Self-attention
- 不过CNN的感受野是人为设计的,而Self-attention的感受野是可学习的参数,并且不会被限制在一个邻域内,而是考虑整张图像上,任何与当前像素点有关的区域。所以,CNN的Function Set是Self-attention的Function Set的子集
- 由于Self-attention的Function Set更大,所以需要的训练数据也更多,否则会导致比CNN更严重的过拟合

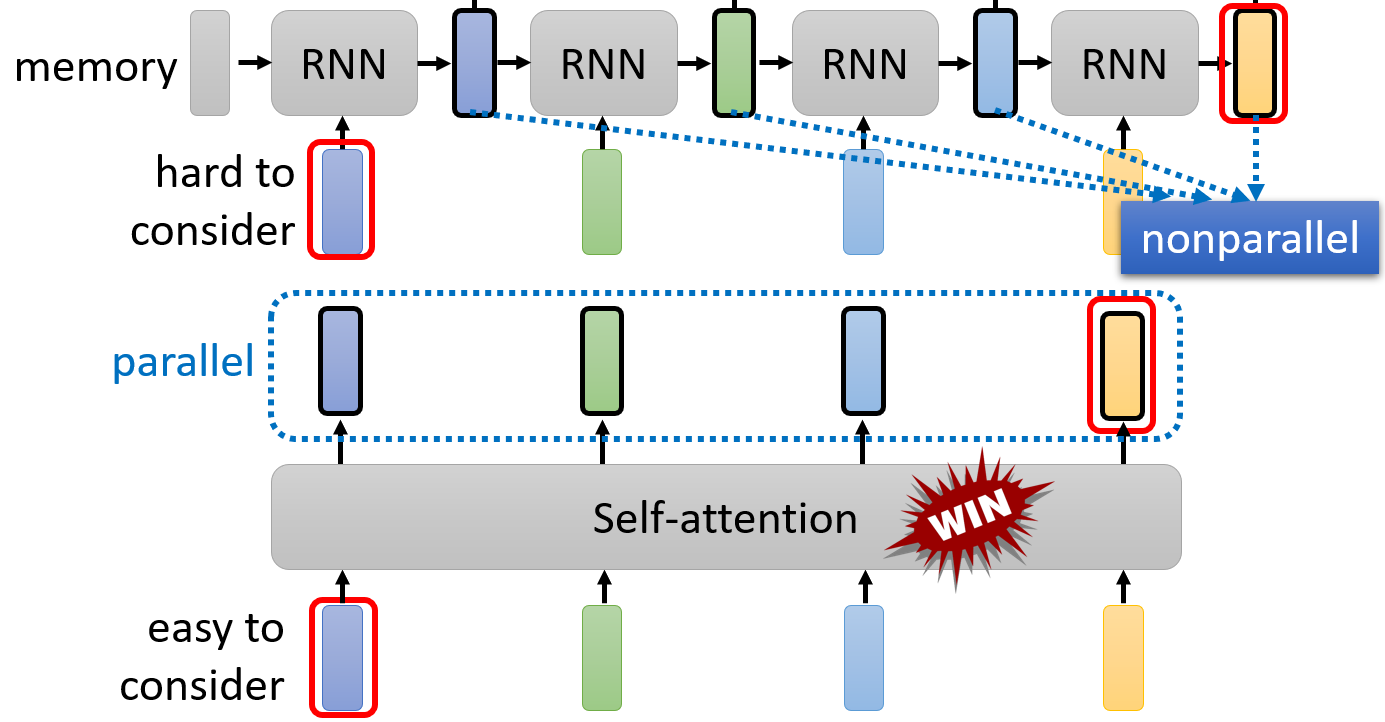
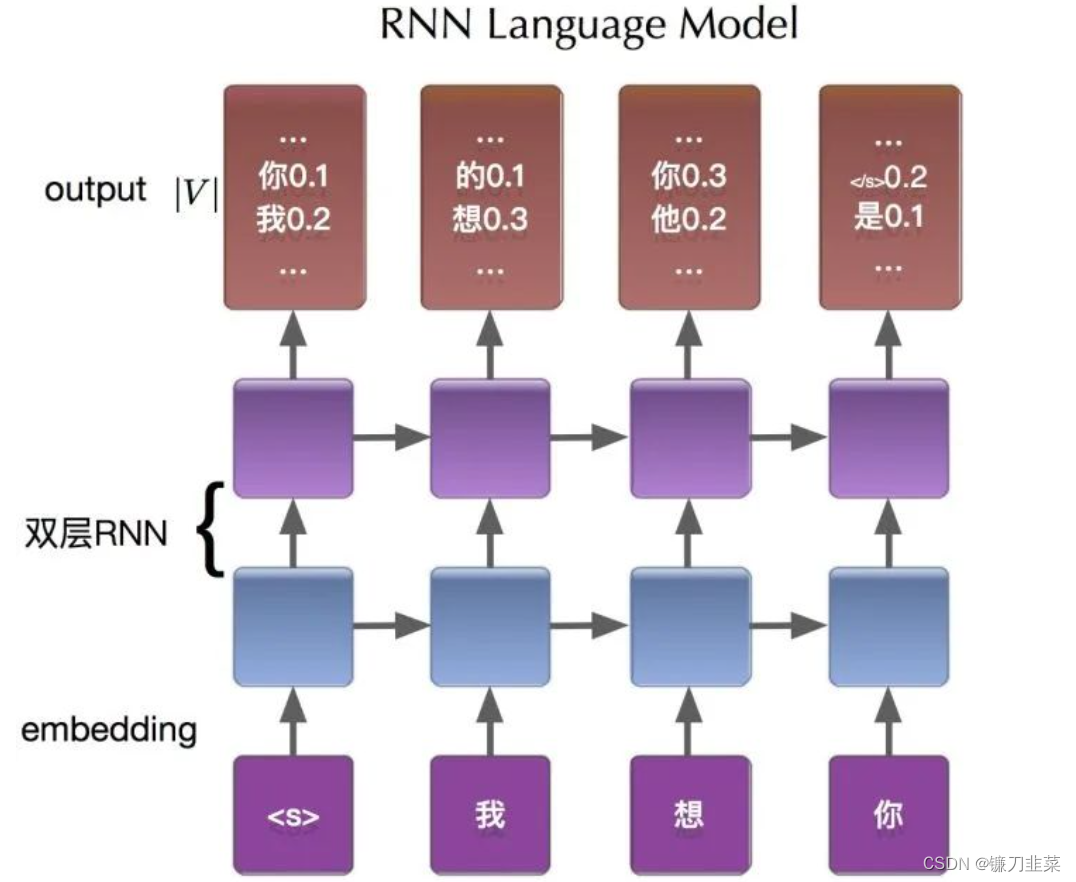
Self-attention VS RNN
- RNN也是用于处理向量序列的神经网络,其特点是
- 存在一些人工设计的状态,这些状态被储存在RNN块内,记忆了当前向量之前的信息
- RNN的当前输出,是之前的“记忆”与当前向量的协同作用,而得到的
- 双向RNN的当前输出,可以看作是考虑了整个输入序列信息的输出
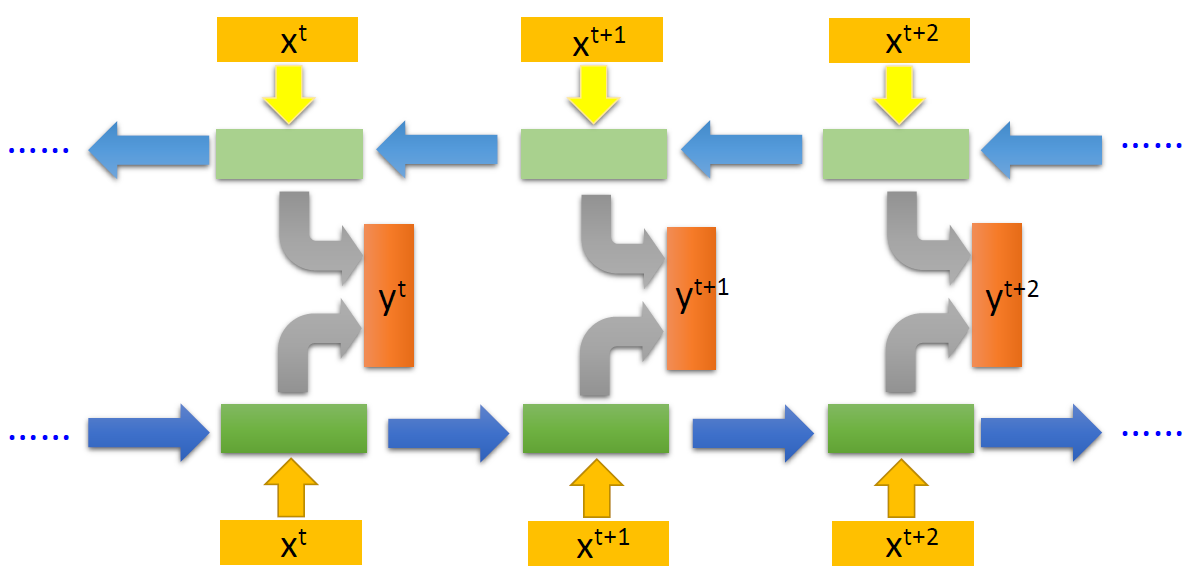
- RNN与Self-attention的区别在于
- RNN的每个输出都不能并行,就像链表一样,逐个计算输出,如果当前向量与之前某一向量非常相关,那么这一相关性信息(value)的提取,只能靠RNN的记忆来建立,因此要求RNN的长期记忆能力
- Self-attention的当前向量,与其他向量计算相关性时,有种“天涯若比邻”的能力,只要具有相关性,就能提取出信息,还能根据相关性的强弱进行加权