在整数规划建模中,经常会使用到0-1变量来辅助建模,将模型表述为IP模型或BIP模型,下面是一些常见的整数规划建模技巧
使用辅助0-1变量实现“非此即彼”约束
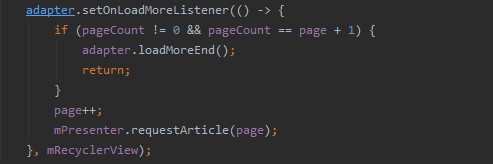
如下图所示,有两条约束,希望只有其中一条起到约束的作用,该怎么处理呢

处理方式如下图,M是一个较大的数,当约束的右边加上M时,无论
x
1
x_1
x1和
x
2
x_2
x2在取在取值范围之内的任意值,式子都是成立的,即该约束无效,没有起到限制变量取值的作用。那么只需要让其中一个约束失效即可,通过在两个约束的右边分别添加
M
y
1
My_1
My1和
M
y
2
My_2
My2,并让
y
1
+
y
2
=
1
y_1+y_2=1
y1+y2=1来实现

保留N个约束中的K个
要保留N个约束中的K个,原理和上面也是相同的,即在每个约束的右边添加
M
y
n
My_n
Myn,然后让
∑
i
=
1
N
y
i
=
N
−
K
\sum_{i=1}^{N}{y_i}=N-K
∑i=1Nyi=N−K即可,这样有
N
−
K
N-K
N−K个约束的右边被添加上了M,这些约束失效,能发挥作用的约束只有K个

函数有N个可能的值
函数有N个可能的值,只需要给每个值乘以一个0-1变量,并通过
∑
i
=
1
N
y
i
=
1
\sum_{i=1}^{N}{y_i}=1
∑i=1Nyi=1让这些值只有一个生效即可

固定收费问题
常见的固定收费问题如:当购买了一个设备之后,首先需要支出设备购买的费用,后续还需要支出设备每个周期的回收费用。通过使用
x
j
≤
M
y
j
x_j\le My_j
xj≤Myj,当
x
j
>
0
x_j>0
xj>0 时,
y
j
=
1
y_j=1
yj=1必须成立,限制函数必须加上一个固定费用
k
j
k_j
kj

二进制表示法代替整数变量
当一个模型存在大量0-1变量和少量整数变量时,无法直接使用高效的BIP算法,这时候可以使用二进制表示法将原有的整数变量分解成多个0-1变量。当一个整数
x
x
x的范围为[0,u]时,可以参考下图的方式将其分解为N个0-1变量

具体的案例如下图所示
分段函数建模
当一个函数是一个分段分数时,即处于不同区域的
x
x
x,其对应的函数表达式
f
(
x
)
f(x)
f(x)是不同的,在处理这种问题的时候,建模的方式如下:
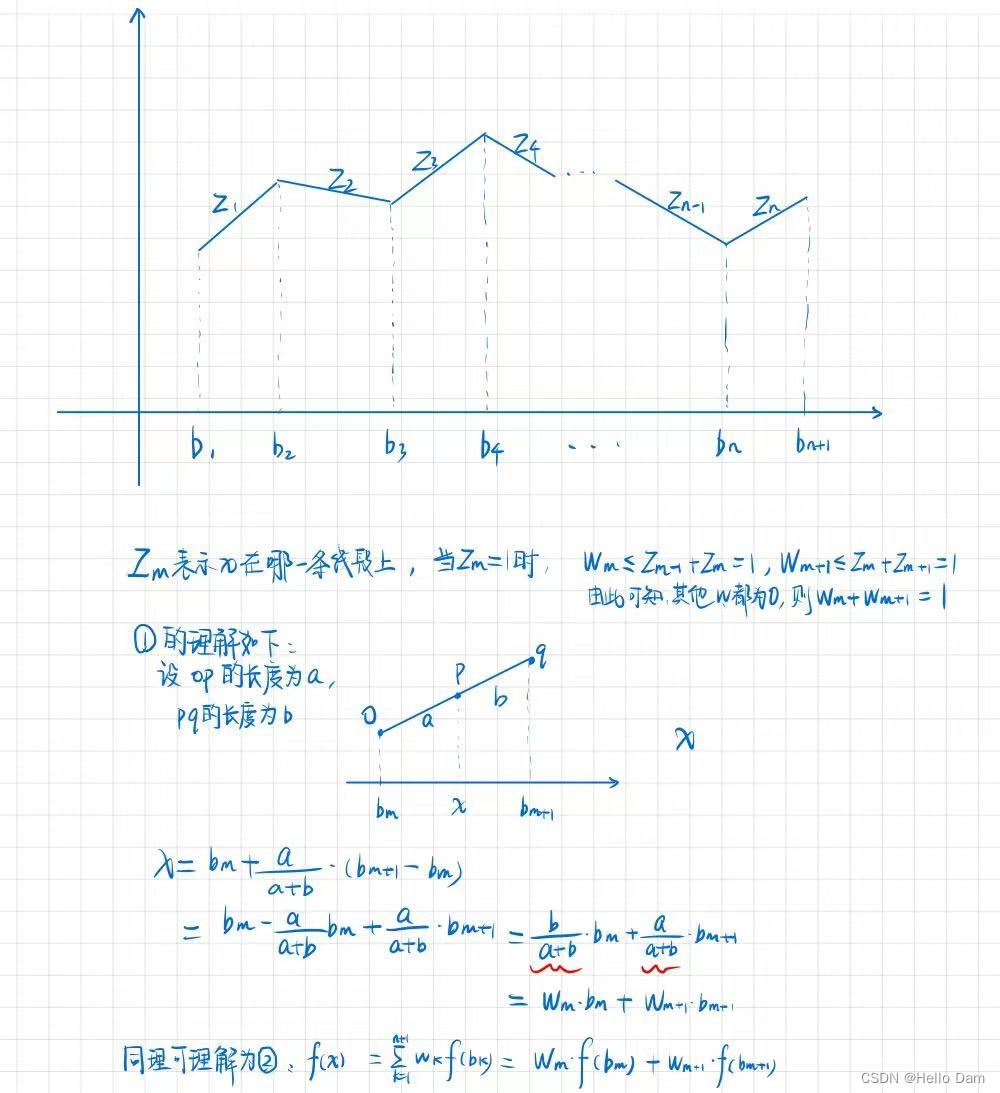
设一个
n
段线性函数
f
(
x
)
的分点为
b
1
≤
⋯
≤
b
n
≤
b
n
+
1
,可以引入
w
k
和
z
k
将
x
和
f
(
x
)
分别表示为
x
=
∑
k
=
1
n
+
1
w
k
b
k
f
(
x
k
)
=
∑
k
=
1
n
+
1
w
k
f
(
b
k
)
其中
w
k
和
z
k
满足下面的关系:
w
1
≤
z
1
,
w
2
≤
z
1
+
z
2
,
⋯
,
w
n
≤
z
n
−
1
+
z
n
,
w
n
+
1
≤
z
n
z
1
+
z
2
+
⋯
+
z
n
=
1
,
z
k
=
0
或
1
w
1
+
w
2
+
⋯
+
w
n
+
1
=
1
,
w
k
≥
0
(
k
=
1
,
2
,
⋯
,
n
+
1
)
\text{设一个}n\text{段线性函数}f\left( x \right) \text{的分点为}b_1\le \cdots \le b_n\le b_{n+1}\text{,可以} \text{引入}w_k\text{和}z_k\text{将}x\text{和}f\left( x \right) \text{分别表示为\\\\\\\\\\\\\\\\\\\\\\\\\ } \\ x=\sum_{k=1}^{n+1}{w_kb_k} \\ f\left( x_k \right) =\sum_{k=1}^{n+1}{w_kf\left( b_k \right)} \\ \text{其中}w_k\text{和}z_k\text{满足下面的关系:} \\ w_1\le z_1,\ w_2\le z_1+z_2,\ \cdots ,\ w_n\le z_{n-1}+z_n,\ w_{n+1}\le z_n \\ z_1+z_2+\cdots +z_n=1,\ z_k=0\text{或}1 \\ w_1+w_2+\cdots +w_{n+1}=1,\ w_k\ge 0\ \left( k=1,2,\cdots ,n+1 \right) \\
设一个n段线性函数f(x)的分点为b1≤⋯≤bn≤bn+1,可以引入wk和zk将x和f(x)分别表示为 x=k=1∑n+1wkbkf(xk)=k=1∑n+1wkf(bk)其中wk和zk满足下面的关系:w1≤z1, w2≤z1+z2, ⋯, wn≤zn−1+zn, wn+1≤znz1+z2+⋯+zn=1, zk=0或1w1+w2+⋯+wn+1=1, wk≥0 (k=1,2,⋯,n+1)
如果无法理解上面的模型处理方式的话,可以仔细理解下面的图片