n−n−皇后问题是指将 nn 个皇后放在 n×nn×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

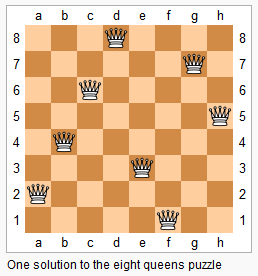
现在给定整数 nn，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 nn。

输出格式

每个解决方案占 nn 行，每行输出一个长度为 nn 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤91≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

思路

深度优先搜索，我们需要排除永远不可能的情况（剪枝），首先是初始化二维数组，把二维数组初始化为'.'

    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            g[i][j]='.';
        }
    }

深度优先搜索分两步走，第一步是判断有没有走到终点，走到终点就输出我们需要的答案

    if(u==n)
    {
        for(int i=0;i<n;i++)    puts(g[i]);
        puts("");
        return;
    }

第二步是遍历每一行，利用条件判断，找到可以符合条件的情况（该题是行，对角线，反对角线不能被使用过），然后改变使用状态，修改字符数组的内容，递归调用dfs函数，恢复现场，把状态和字符数组的内容都修改回来

    int x=u;
    for(int y=0;y<n;y++)
    {
        if(!col[y]&&!dg[y+x]&&!udg[y-x+n])
        {
            col[y]=dg[y+x]=udg[y-x+n]=true;
            g[x][y]='Q';
            dfs(x+1);
            col[y]=dg[y+x]=udg[y-x+n]=false;
            g[x][y]='.';
        }
    }

这里把u和i更换成了x和y，感觉更加方便理解

代码

#include<bits/stdc++.h>
using namespace std;

int n;
const int N=20;
char g[N][N];
bool col[N],dg[N],udg[N];

void dfs(int u)
{
    if(u==n)
    {
        for(int i=0;i<n;i++)    puts(g[i]);
        puts("");
        return;
    }
    
    int x=u;
    for(int y=0;y<n;y++)
    {
        if(!col[y]&&!dg[y+x]&&!udg[y-x+n])
        {
            col[y]=dg[y+x]=udg[y-x+n]=true;
            g[x][y]='Q';
            dfs(x+1);
            col[y]=dg[y+x]=udg[y-x+n]=false;
            g[x][y]='.';
        }
    }
}

int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            g[i][j]='.';
        }
    }
    dfs(0);
    return 0;
}