文章来源于极客时间前google工程师−王争专栏。
如何实现随机访问?
什么是数组?
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
- 线性表,顾名思义,线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
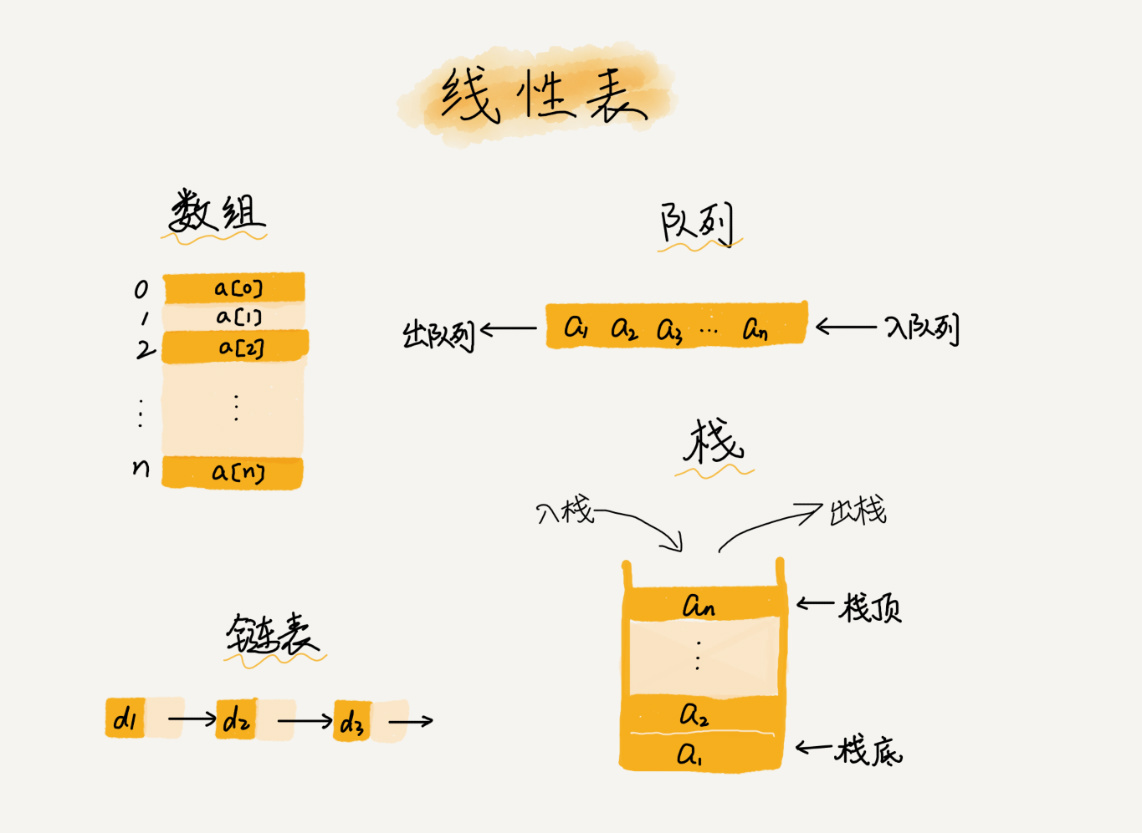
- 非线性表,比如二叉树、堆、图等。在非线性表中,数据之间并不是简单的前后关系。

- 连续的内存空间和相同的类型的数据。 正因为这两个限制,它才有了一个堪称“杀手锏”的特性:“随机访问”。但有利就有弊,这两个限制也让数组的很多操作变得非常低效,比如要想在数组中删除、插入一个数据,为了保证数据连续性,就需要做大量的数据搬移工作。
数组如何实现根据下标随机访问数组?
以int[] a = new int[10]来举例。计算机给数组a,分配了一块连续的内存空间1000~1039,其中内存块的首地址为base_address = 1000。

我们知道,计算机会给每个内存单元分配一个地址,计算机通过地址来访问内存中的数据。当计算机需要随机访问数组中的某个元素时,它会受限通过下面的寻址公式,计算出该元素存储的内存地址:
a[i]_address = base_address + i*data_type_size
错误纠正
- 链表适合插入、删除,时间复杂度为O(1);数组适合查找,查找时间复杂度为O(1)
- 数组是适合查找操作,但是查找的时间复杂度不为O(1)。即便是排好序的数组,用二分查找,时间复杂度也是O(logn)。所以,正确的表述应该是,数组支持随机访问,根据下标随机访问的时间复杂度为O(1)。
低效的“插入”和“删除”
数组为了保持内存数据的连续性,会导致插入、删除两个操作比较低效。
插入操作
假设数组的长度为n,现在,如果我们需要将一个数据插入到数组中的第k个位置。为了把第k个位置腾出来,给新来的数据,需要将第k~n这部分的元素都顺序地往后挪一位。
- 最好:O(1)
- 最坏:O(n)
- 平均:O(n)

图上处理,会将第k个位置插入一个元素的时间复杂度降为O(1)。这个处理思想在快排中也会用到。
删除操作
- 最好:O(1)
- 最坏:O(n)
- 平均:O(n)
实际上,在某些特殊场景下,并不一定非得追求数组中数据的连续性。如果我们将多次删除操作集中在一起执行,删除的效率会不会提高很多呢?
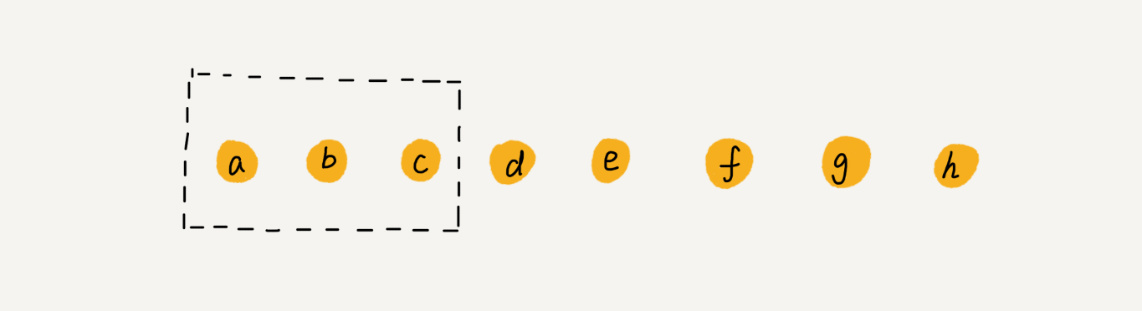
每次的删除操作并不是真正地搬移数据,只是记录数据已经被删除。当数组中没有更多空间存储数据时,我们再触发执行一次真正地删除操作,这样就大大减少了删除操作导致的数据搬移。
这就是JVM标记清除垃圾回收算法的核心思想。
警惕数组的访问越界问题
如下c语言代码运行结果:
int main(int argc,char* argv[]){
int i = 0;
int arr[3] = {0};
for(;i<=3;i++){
arr[i] = 0;
printf("hello world");
}
return 0;
}
在 C 语言中,只要不是访问受限的内存,所有的内存空间都是可以自由访问的。根据我们前面讲的数组寻址公式,a[3]也会被定位到某块不属于数组的内存地址上,而这个地址正好是存储变量i的内存地址,那么 a[3]=0 就相当于i=0,所以所以就会导致代码无限循环。
容器能否完全替代数组?
- java ArrayList无法存储基本类型,比如int、long,需要封装为Integer、Long类,而autoboxing、unboxing则有一定的性能消耗,所以如果特别关注性能,或者使用基本类型,就可以选择数组。
- 如果数据大小事先已知,并且对数据的操作非常简单,用不到ArrayList提供的大部分方法,也可以直接使用数组。
- 当要表示多维数组时,用数组往往会更加直观。比如Object[][] array;而用容器的话需要定义:ArrayList array。
- 对于业务开发,直接使用容器就足够了,省时省力。毕竟损耗一丢丢性能,完全不会影响到系统整体的性能。
- 底层开发,比如开发网络框架,性能的优化需要做到机制,这个时候数组就会优于容器,成为首选。
解答开篇
数组为什么要从0开始编号,而不是从1开始呢?
- 从0开始
- 计算a[k]的内存地址公式如下:
a[k]_address = base_address+k*data_type_size
- 从1开始
- 计算a[k]的内存地址公式如下:
a[k]_address = base_address+(k-1)*data_type_size
通过比较发现,如果从1开始编号,每次随机访问数组元素都会多一次减法运算,对于CPU来说,就是多了一次减法指令。
很多语言也并不是从0开始计数的,比如Matlab。甚至支持负数下标,比如Python。
二维数组的寻址公式
a[][] array = int[m][n];
(i<m,j<n)
a[i][j]_address = base_address+i*n*data_base_type+j*data_base_type
a[i][j]_address = base_address+(i*n+j)*data_base_type