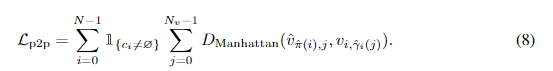0. 简介
最近环视图像处理其实已经非常火了,最近地平线&华科则是提出了一种新的环视车道线地图提取工具。高清(HD)地图提供了驾驶场景丰富而精确的环境信息,是自动驾驶系统规划中基础且不可或缺的组成部分。《MapTR: Structured Modeling and Learning for Online Vectorized HD Map Construction》提出了一种用于高效在线矢量化HD地图构建的结构化端到端Transformer。通过统一的置换等价建模方法,即将地图元素建模为一个具有一组等价置换的点集,准确描述了地图元素的形状并稳定了学习过程。文中使用统一的置换等价建模方法,即将地图元素建模为一个具有一组等价置换的点集,准确描述了地图元素的形状并稳定了学习过程。相关的代码已经在Github上开源了。
1. 文章贡献

图1. MapTR在复杂和多样的驾驶场景中保持了稳定而强健的矢量化高清地图构建质量
本文的贡献可以总结如下:
- 我们提出了一种统一的置换等价建模方法,用于地图元素,即将地图元素建模为一个具有一组等价置换的点集,准确描述了地图元素的形状并稳定了学习过程。
- 基于这种创新的建模方法,我们提出了MapTR,一个用于高效在线矢量化高清地图构建的结构化端到端框架。我们设计了一种层次化查询嵌入方案,以灵活地编码实例级和点级信息,进行地图元素的层次双向匹配学习,并通过提出的点对点损失和边方向损失在点和边的级别上监督几何形状。
- MapTR是第一个在复杂和多样的驾驶场景中具有稳定而强健性能的实时和最先进的矢量化高清地图构建方法。
2. MAPTR置换等价建模
MapTR旨在以统一的方式对高清地图进行建模和学习。高清地图是由矢量化的静态地图元素组成,包括人行横道、车道分隔线、道路边界等。为了进行结构化建模,MapTR将地图元素几何地抽象为闭合形状(如人行横道)和开放形状(如车道分隔线)。通过沿着形状边界顺序采样点,闭合形状元素被离散化为多边形,而开放形状元素被离散化为折线。
一开始,多边形和折线都可以表示为有序点集 V F = [ v 0 , v 1 , . . . , v N v − 1 ] V^F = [v_0, v_1, . . . , v_{N_v −1}] VF=[v0,v1,...,vNv−1](见图3(Vanilla))。 N v N_v Nv表示点的数量。然而,点集的排列没有明确定义,也不唯一。多边形和折线存在许多等价的排列方式。例如,如图2(a)所示,对于两条相对车道之间的车道分隔线(折线),很难定义其方向。车道分隔线的两个端点都可以视为起点,点集可以按两个方向进行组织。在图2(b)中,对于人行横道(多边形),**点集可以按两个相反的方向(顺时针和逆时针)进行组织。**而且,循环改变点集的排列对多边形的几何形状没有影响。对点集施加固定的排列作为监督是不合理的。这种固定的排列与其他等价的排列相矛盾,阻碍了学习过程。
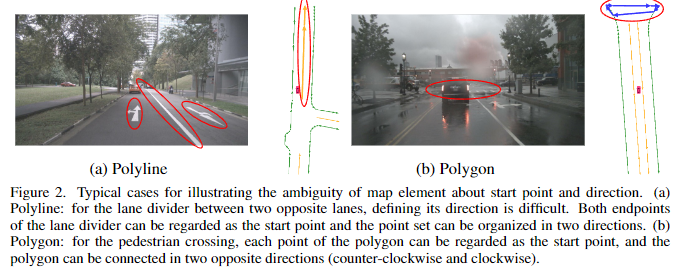
图2. 用于说明地图元素关于起点和方向模糊性的典型案例。(a) 折线:对于两条相对车道之间的车道分隔线,定义其方向是困难的。车道分隔线的两个端点都可以被视为起点,并且点集可以按两个方向进行组织。(b) 多边形:对于人行横道,多边形的每个点都可以被视为起点,并且多边形可以按两个相反的方向(顺时针和逆时针)连接。
为了弥合这一差距,MapTR用 V = ( V , Γ ) V = (V, Γ) V=(V,Γ)来对每个地图元素进行建模。 V = { v j } j = 0 N v − 1 V = \{v_j\}^{N_v −1}_{j=0} V={vj}j=0Nv−1表示地图元素的点集( N v N_v Nv是点的数量)。 Γ = γ k Γ = {γ^k} Γ=γk表示点集 V V V的一组等价排列,覆盖了所有可能的组织顺序。
具体而言,对于折线元素(见图3(左)),
Γ
Γ
Γ包括两种等价排列方式。
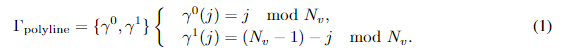
对于多边形元素(见图3(右)),
Γ
Γ
Γ包括
2
×
N
v
2 × N_v
2×Nv种等价排列方式。
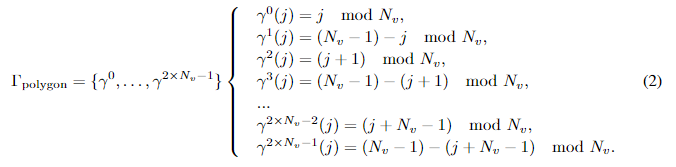
通过引入等价排列的概念,MapTR以统一的方式对地图元素进行建模,并解决了模糊性问题。MapTR进一步引入了层次化的双向匹配(详见第3节和第4节)进行地图元素学习,并设计了一个结构化的编码器-解码器Transformer架构以高效预测地图元素(详见第5节)。
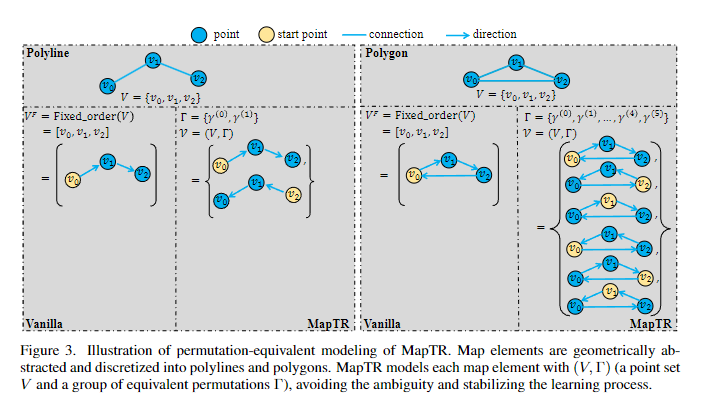
图3. MapTR的置换等价建模示意图。地图元素被几何地抽象化并离散化为折线和多边形。MapTR用 ( V , Γ ) (V, Γ) (V,Γ)(一个点集 V V V和一组等价排列 Γ Γ Γ)来对每个地图元素进行建模,避免了模糊性并稳定了学习过程。
3. 层次匹配(重要内容)
MapTR在单次传递中并行推断一组固定大小的 N N N个地图元素,遵循DETR(Carion等,2020; Fang等,2021)的端到端范例。 N N N被设定为大于场景中地图元素的典型数量。我们用 Y ^ = { y ^ i } i = 0 N − 1 \hat{Y} = \{\hat{y}_i\}^{N −1}_{i=0} Y^={y^i}i=0N−1 表示 N N N个预测地图元素的集合。将地面实况(GT)地图元素集合填充为具有大小 N N N的集合,用 Y = { y i } i = 0 N − 1 Y = \{y_i\}^{N −1}_{i=0} Y={yi}i=0N−1 表示。其中, y i = ( c i , V i , Γ i ) y_i = (c_i, V_i, Γ_i) yi=(ci,Vi,Γi), c i c_i ci、 V i V_i Vi和 Γ i Γ_i Γi分别是GT地图元素 y i y_i yi的目标类别标签、点集和排列组。 y ^ i = ( p ^ i , V ^ i ) \hat{y}_i = (\hat{p}_i, \hat{V}_i) y^i=(p^i,V^i), p ^ i \hat{p}_i p^i和 V ^ i \hat{V}_i V^i分别是预测的分类得分和预测的点集。为了实现结构化的地图元素建模和学习,MapTR引入了层次化的双向匹配,即按照顺序进行实例级匹配和点级匹配。
3.1 实例级匹配
首先,我们需要在预测的地图元素
{
y
^
i
}
\{\hat{y}_i\}
{y^i}和GT地图元素
{
y
i
}
\{y_i\}
{yi}之间找到最优的实例级标签分配
π
^
\hat{π}
π^。
π
^
\hat{π}
π^是N个元素的排列(
π
^
∈
Π
N
\hat{π} ∈ Π_N
π^∈ΠN ),具有最低的实例级匹配成本:
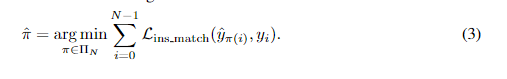
L_{ins_match}(\hat{y}_π(i),y_i)是预测
y
^
π
(
i
)
\hat{y}π(i)
y^π(i)和GT
y
i
y_i
yi之间的逐对匹配成本,它考虑了地图元素的类别标签和点集位置。
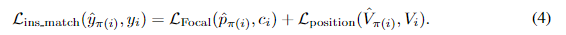
L
F
o
c
a
l
(
p
^
π
(
i
)
,
c
i
)
L_{Focal}(\hat{p}_π(i),c_i)
LFocal(p^π(i),ci)是类别匹配成本项,定义为预测的分类得分
∣
h
a
t
p
π
(
i
)
|hat{p}_{π(i)}
∣hatpπ(i)和目标类别标签
c
i
c_i
ci之间的Focal损失(Lin等,2017)。
L
p
o
s
i
t
i
o
n
(
V
^
π
(
i
)
,
V
i
)
L_{position}(\hat{V}_{π(i)},V_i)
Lposition(V^π(i),Vi)是位置匹配成本项,反映了预测的点集
V
^
π
(
i
)
\hat{V}_{π(i)}
V^π(i)和GT点集
V
i
V_i
Vi之间的位置相关性。使用匈牙利算法在DETR中寻找最优的实例级分配
π
^
\hat{π}
π^。
3.2 点级匹配
在实例级匹配之后,每个预测的地图元素
y
^
π
^
(
i
)
\hat{y}_{\hat{π}(i)}
y^π^(i)与一个GT地图元素
y
i
y_i
yi进行匹配。然后,对于每个被分配了正类别标签(
c
i
≠
∅
c_i \neq ∅
ci=∅)的预测实例,我们进行点级匹配,以找到预测点集
V
^
π
^
(
i
)
\hat{V}_{\hat{π}(i)}
V^π^(i)和GT点集
V
i
V_i
Vi之间的最优点对点分配
γ
^
∈
Γ
\hat{γ} ∈ Γ
γ^∈Γ。
γ
^
\hat{γ}
γ^从预定义的排列组
Γ
Γ
Γ中选择,具有最低的点级匹配成本。
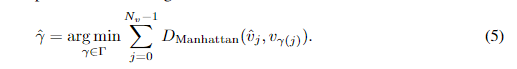
D
M
a
n
h
a
t
t
a
n
(
v
^
j
,
v
γ
(
j
)
)
D_{Manhattan}(\hat{v}_j, v_{γ(j)})
DManhattan(v^j,vγ(j))是预测点集
V
^
\hat{V}
V^的第
j
j
j个点与GT点集
V
V
V的第
γ
(
j
)
γ(j)
γ(j)个点之间的曼哈顿距离。
4. 训练损失
MapTR基于最优的实例级和点级分配(
π
^
\hat{π}
π^和
{
γ
^
i
}
\{\hat{γ}_i\}
{γ^i})进行训练。损失函数由三个部分组成,包括分类损失、点对点损失和边方向损失。
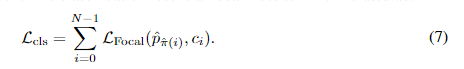
4.1 点对点损失
点对点损失用于监督每个预测点的位置。对于具有索引
i
i
i的每个GT实例,根据点级最优匹配结果
γ
^
i
\hat{γ}_i
γ^i,将每个预测点
v
^
π
^
(
i
)
,
j
\hat{v}_{\hat{π}(i),j}
v^π^(i),j分配给一个GT
v
i
,
γ
^
i
(
j
)
v_{i,\hat{γ}_i(j)}
vi,γ^i(j)。点对点损失定义为计算每个配对点之间的曼哈顿距离: