文章前言：如果有小白同学还是对于二叉树不太清楚，作者推荐：二叉树的初步认识_加瓦不加班的博客-CSDN博客

二叉树最大深度-力扣 104 题

 

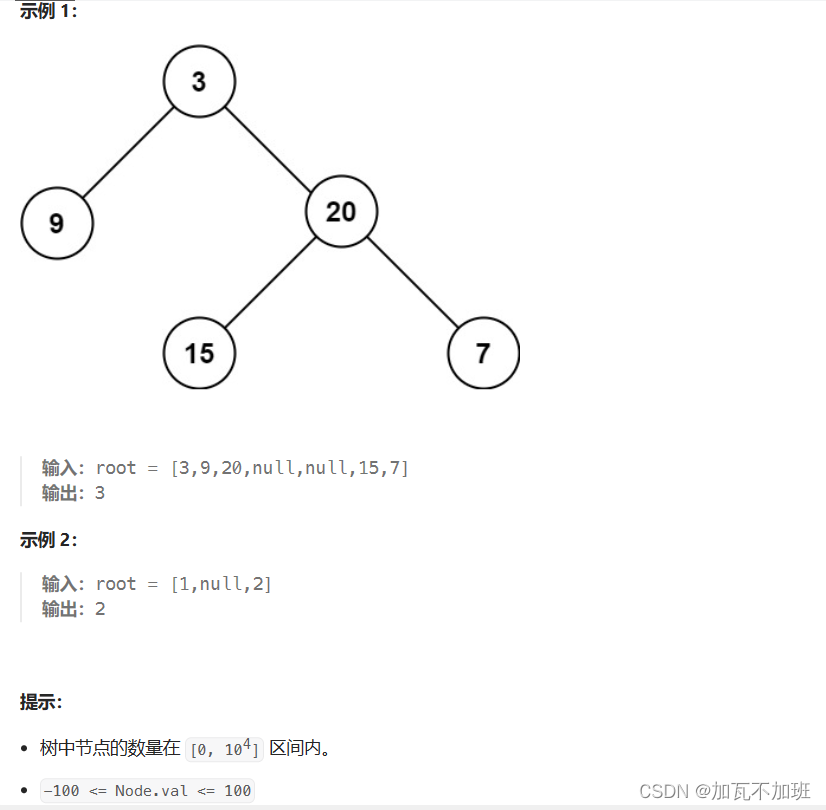
（不知道“后序遍历”的小白同学，请先看：二叉树的初步认识_加瓦不加班的博客-CSDN博客）

后序遍历求解-递归

/*
    思路：
    1. 得到左子树深度, 得到右子树深度, 二者最大者加一, 就是本节点深度
    2. 因为需要先得到左右子树深度, 很显然是后序遍历典型应用
    3. 关于深度的定义：从根出发, 离根最远的节点的总边数,这个总边数指的就是下面的线段数
        注意: 力扣里的深度定义要多一,在你现在看来下面的深度确实是1 2 0  但是力扣官方觉得：在你看来的基础上+1才是正确的深度

  你的视角：      深度:1         深度:2         深度:0
  力扣的视角：      深度:2         深度:3         深度:1
                    1            1            1
                   / \          / \
                  2   3        2   3
                                    \
                                     4
 */
public int maxDepth(TreeNode node) {
    if (node == null) {
        return 0; // 非力扣题目改为返回 -1
    }
    int d1 = maxDepth(node.left);
    int d2 = maxDepth(node.right);
    return Integer.max(d1, d2) + 1;
}

后序遍历求解-非递归

/*
    思路：
    1. 使用非递归后序遍历, 栈的最大高度即为最大深度
 */
public int maxDepth(TreeNode root) {
    TreeNode curr = root;
    LinkedList<TreeNode> stack = new LinkedList<>();
    int max = 0;
    TreeNode pop = null;
    while (curr != null || !stack.isEmpty()) {
        //先访问左子树
        if (curr != null) {
            //访问左子树时记得压栈
            stack.push(curr);
            //通过栈的大小来记录其最大深度
            int size = stack.size();
            if (size > max) {
                max = size;
            }
            curr = curr.left;
        } else {
            TreeNode peek = stack.peek();
            if(peek.right == null || peek.right == pop) {
                pop = stack.pop();
            } else {
                curr = peek.right;
            }
        }
    }
    return max;
}

层序遍历求解

/*
    思路：
    1. 使用层序遍历, 层数即最大深度
 */
public int maxDepth(TreeNode root) {
    if(root == null) {
        return 0;
    }
    //LinkedList既可以做为双向链表、队列、栈
    Queue<TreeNode> queue = new LinkedList<>();
    //将根节点加入到队列中
    queue.offer(root);
    int level = 0;//深度
    //不断从队列的头部取出元素,然后把其子节点加入到队列中
    while (!queue.isEmpty()) {
        level++;
        int size = queue.size();//获取每层节点个数
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
    return level;
}