102. 二叉树的层序遍历 - 力扣（LeetCode）
如图：层序遍历即一层一层遍历，从左到右。
先遍历第一层，把第一层的节点放到队列里面，levesize=q.size()，即代表队列里面有多少个值。
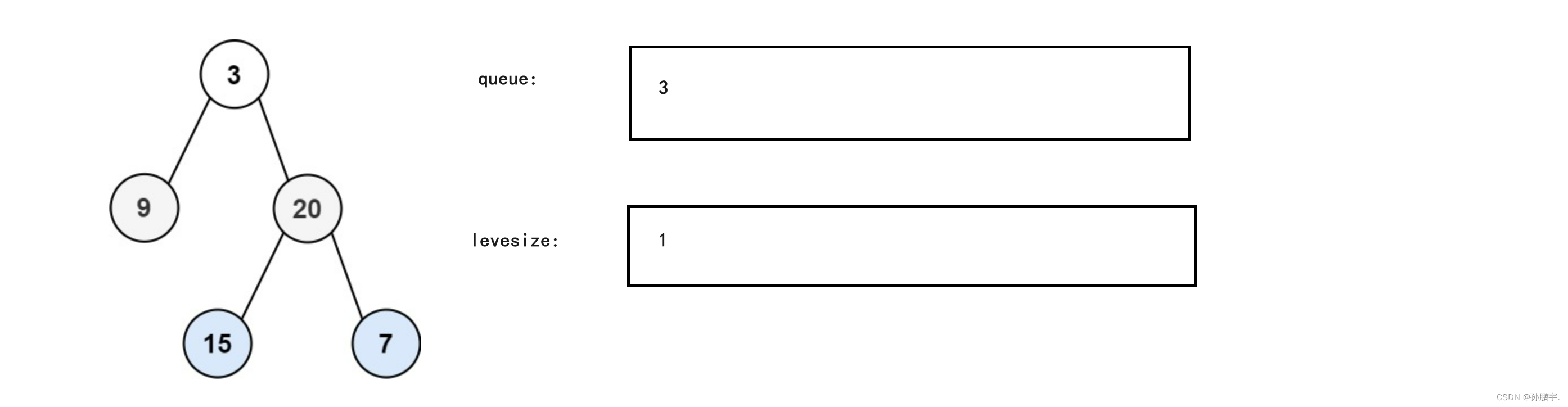
然后现在把队里里面的值清空，放到vector里面(每一层的值都放一个vectot里面）。再把第二层的节点传到队列里面。levesize也根据队列的size产生变化：
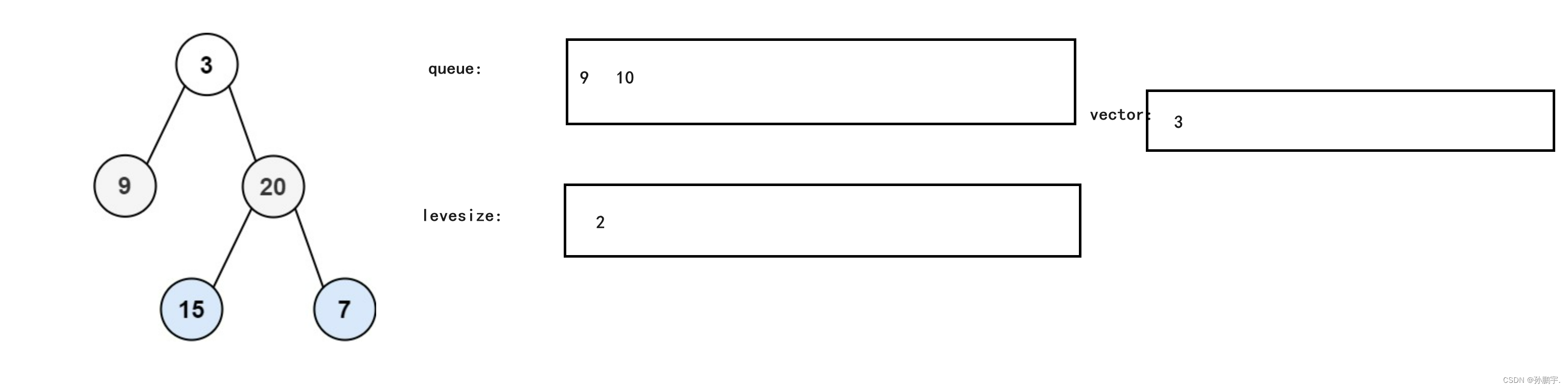
以此类推,最终效果为：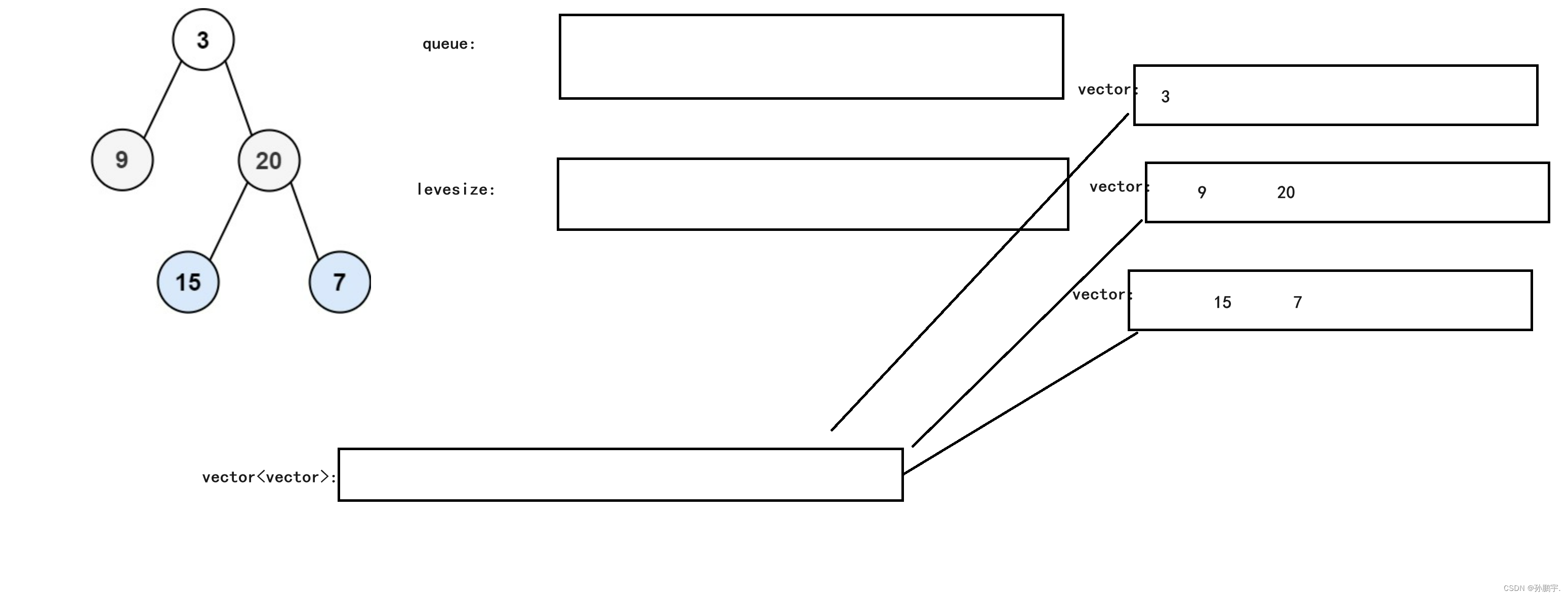
代码：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;//套用树模版来个队列
vector<vector<int>> vv;//最后把遍历完的数据放到vv里
int levesize=0;
if(root) q.push(root);
levesize=1;
while(!q.empty())//当队列不为空时
{ vector<int> v;
while(levesize--)
{
TreeNode* Front=q.front();
q.pop();
v.push_back(Front->val);
if(Front->left) q.push(Front->left);
if(Front->right) q.push(Front->right);
}
levesize=q.size();
vv.push_back(v);
}
return vv;
}
};150. 逆波兰表达式求值 - 力扣（LeetCode）
这道题实际上就用后缀和去实现运算：
平时我们的运算都是中缀运算，如1+2*3，1+2是不能先算的，因为我们不能确定后面操作符，后面操作符的优先级如果比“+”优先级大那么1+2就不能 先运算，应该先运算2*3，然后得到的结构再去+1.
列如我们有一个这样的式子：((2 + 1) * 3) = 9。如果用后缀运算，就是把
((2 + 1) * 3) = 9变换成2 1 + 3 *。
至于怎么变成后缀的，这道题已经帮我们编好了，我们只需要把它编好的数据入栈就行了：
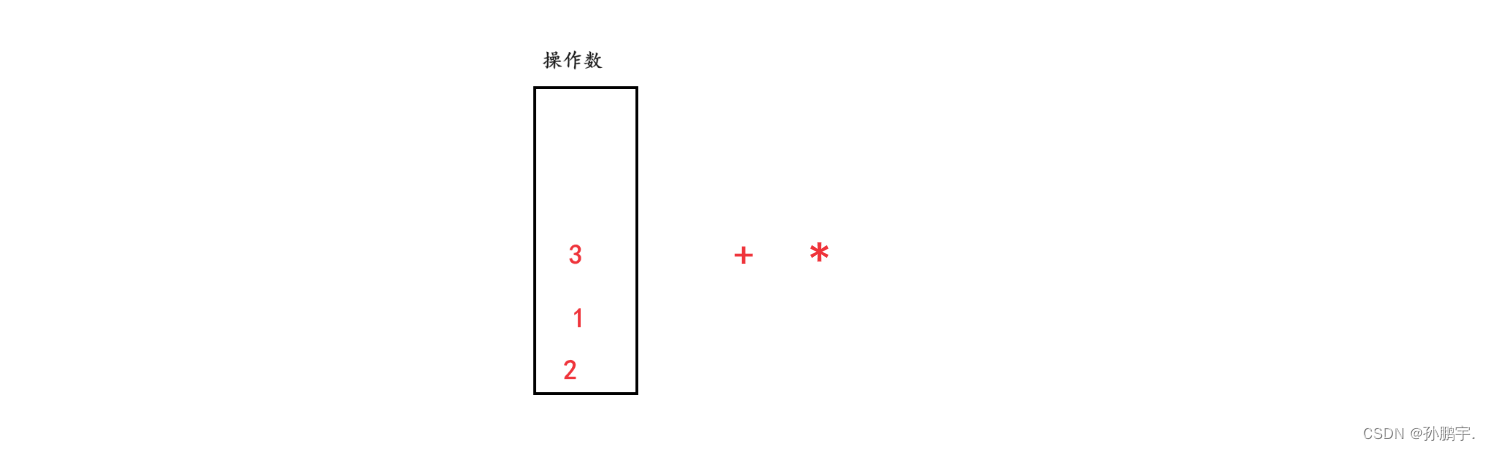然后后进先出，先从操作数里取两个数出来，为什么取两个出来呢？因为一个操作符肯定需要两个操作数进行操作。然后操作完之后再入栈：
代码：
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto str:tokens)
{
if( str=="+"
||str=="-"
||str=="*"
||str=="/"
)
{
int right=st.top();
st.pop();
int left=st.top();
st.pop();
switch(str[0])
{
case '+':
st.push(left+right);
break;
case '-':
st.push(left-right);
break;
case '*':
st.push(left*right);
break;
case '/':
st.push(left/right);
break;
}
}
else
{
st.push(stoi(str));
}
}
return st.top();
}
};模拟实现一下栈，然后测一下上面这个逆波兰表达式：
首先把写一个模版，这个模版里面我们除了放T这个类型之外还要再放个参数：Container，这个参数就是我们可以把vector,list等其他容易作为这个栈的底层，这个栈可以用其他容器的push_back,pop_back,size()等函数。
写一下函数的定义：
main函数把逆波兰那道题的代码复制过来：
然后写一个测试用例：
传一个vector作为底层：
运行：
传list作为底层：
运行：
写一段如下代码验证一下deque sort和vector sort占用栈帧情况对比：
void test2()
{
srand((size_t)time(0));
const size_t N = 100000;
vector<int> v;
deque<int> dq;
v.reserve(N);
for (size_t i = 0; i < N; i++)
{
auto e = rand;
v.push_back((int)e);
dq.push_back((int)e);
}
int begin1 = clock();
sort(v.begin(), v.end());
int end1 = clock();
int begin2 = clock();
sort(dq.begin(), dq.end());
int end2 = clock();
cout << "vector sort:" << end1 - begin1 << endl;
cout << "deque sort:" << end2 - begin2 << endl;
}
然后再把deque给vector来跑
void test2()
{
srand((size_t)time(0));
const size_t N = 100000;
vector<int> v;
deque<int> dq;
v.reserve(N);
for (size_t i = 0; i < N; i++)
{
auto e = rand;
v.push_back((int)e);
dq.push_back((int)e);
}
int begin1 = clock();
sort(v.begin(), v.end());
int end1 = clock();
int begin2 = clock();
v.assign(dq.begin(), dq.end());
sort(v.begin(), v.end());
int end2 = clock();
cout << "vector sort:" << end1 - begin1 << endl;
cout << "deque sort:" << end2 - begin2 << endl;
}
queue.h
#pragma once
#include<iostream>
#include<deque>
namespace bitt
{ template<class T, class Container = deque<T>>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
const T& front()
{
return _con.front();
}
const T& back()
{
return _con.back();
}
bool empty()
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
}main
void test_queue()
{
bitt:: queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
q.push(5);
while(!q.empty())
{
cout << q.front()<<" ";
q.pop();
}
cout << endl;
}
int main()
{
test_queue();
}
