583. 两个字符串的删除操作

Leetcode

思路

1. dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。
2. 递推公式：
   • 当word1[i - 1] 与 word2[j - 1]相同的时候
     • dp[i][j] = dp[i - 1][j - 1]
   • 当word1[i - 1] 与 word2[j - 1]不相同的时候
     • 删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
     • 删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
     • 同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
     • 总的来说就是取最小值，所以是dp[i][j] = min(dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1)
     • 因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2，所以递推公式可简化为：dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)
3. 初始化：dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i][0] = i。dp[0][j]的话同理
4. 从上到下，从左到右
5. 以word1:“sea”，word2:"eat"为例，推导dp数组状态图如下：
   

思路2

和1143.最长公共子序列 基本相同，只要求出两个字符串的最长公共子序列长度即可，那么除了最长公共子序列之外的字符都是必须删除的，最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。

代码

思路一

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [[0] * (len(word1) + 1) for _ in range(len(word2) + 1)]

        for i in range(len(word2) + 1):
            dp[i][0] = i
        for j in range(len(word1) + 1):
            dp[0][j] = j

        for i in range(1, len(word2) + 1):
            for j in range(1, len(word1) + 1):
                if word1[j - 1] == word2[i - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)

        return dp[-1][-1]

• 时间复杂度: O(n * m)
• 空间复杂度: O(n * m)

72. 编辑距离

Leetcode

思路

1. dp数组含义：dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
2. 递推公式。编辑存在以下几种操作：

   if (word1[i - 1] == word2[j - 1])
       不操作
   if (word1[i - 1] != word2[j - 1])
       增
       删
       换
   

   • 不操作：无需编辑，直接取去掉i-1, j-1的最小编辑距离 dp[i][j] = dp[i - 1][j - 1]
   • 增和删本质上是一样的，同一种操作的正反向，可以是删word1的元素，也可以是删word2的元素
     • 删掉word1 i-1 元素的最小编辑距离：dp[i][j] = dp[i - 1][j ] + 1
     • 删掉word2 j-1 元素的最小编辑距离：dp[i][j] = dp[i][j - 1] + 1
   • 替换：
     • 首先我们要明白为什么替换不能被删除给替代。举个例子“abc”和“abg”，如果分别删除“c”和“g”的话需要两步操作，但是如果替换“c”为“g”的话只需要一步。
     • 所以替换的递推公式就是在“ab”和“ab”两个子串的最小编辑距离上加一
     • 具体为dp[i][j] = dp[i - 1][j - 1] + 1
3. 初始化：
   dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。
   那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i，同理dp[0][j] = j。
4. 遍历顺序：从上到下，从左到右
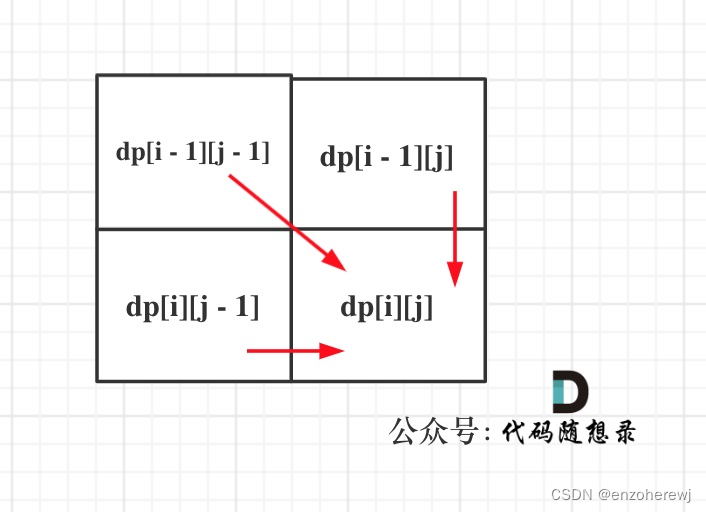
5. 举例推导：以示例1为例，输入：word1 = “horse”, word2 = "ros"为例，dp矩阵状态图如下：
   

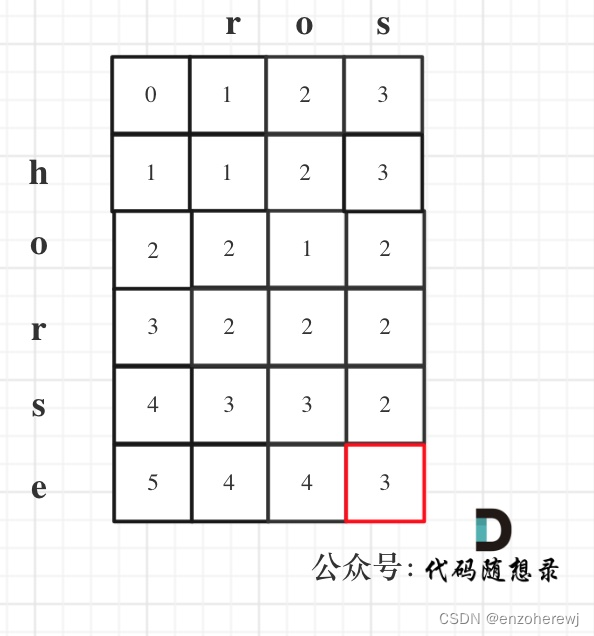
代码

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [[0] * (len(word1) + 1) for _ in range(len(word2) + 1)]

        for i in range(len(word2) + 1):
            dp[i][0] = i
        
        for j in range(len(word1) + 1):
            dp[0][j] = j
        
        for i in range(1, len(word2) + 1):
            for j in range(1, len(word1) + 1):
                if word2[i - 1] == word1[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1], dp[i][j - 1]) + 1
                
        return dp[-1][-1]

• 时间复杂度: O(n * m)
• 空间复杂度: O(n * m)